Глава 9. Коллигативные свойства растворов

После изучения этой темы вы должны:

иметь представления о следующих понятиях и явлениях:

- осмос, осмотическое давление (закон Вант-Гоффа), его роль.

- закон Рауля о давлении паров растворителя над раствором и изменении температур кипения и замерзания растворов (следствия закона Рауля).

Коллигативные свойства – это свойства, которые не зависят от природы частиц растворенного вещества, а зависят только от концентрации частиц в растворе. Коллигативными свойствами разбавленных растворов являются:

- скорость диффузии

- осмотическое давление (Закон Вант-Гоффа)

- давление насыщенного пара растворителя над раствором (Закон Рауля)

- температура кипения раствора (1следствие из закона Рауля)

- температура кристаллизации раствора (2 следствие из закона Рауля)

Свойства неэлектролитов

Осмосом называется самопроизвольное перемещение молекул растворителя через полупроницаемую мембрану из раствора меньшей концентрации в раствор большей концентрации. В результате протекания осмоса возникает осмотическое давление раствора. Гипертоническим раствором называют тот раствор, у которого осмотическое давление больше. Гипотоническим раствором – раствор с меньшим осмотическим давлением. Изотоничные растворы – это растворы с одинаковой величиной осмотического давления.

	Растительная клетка (С >) (внутриклеточный раствор)		Мем-брана		Внешняя среда (С <) (межклеточный раствор)

Н₂О Н₂О

Вант-Гофф, изучая зависимость осмотического давления от внешних факторов установил, что оно не зависит от природы растворенного вещества, а зависит только от числа частиц в растворе и от температуры:

Р_осм= СмRT, где Росм [кПа], T [K]- абсолютная температура, R=8,32 кДж/моль - универсальная газовая постоянная, См - молярная концентрация раствора [моль/л].

Осмотическое давление раствора, содержащего несколько веществ, равно сумме осмотических давлений, вызываемых каждым из них.

Давление насыщенного пара растворителя над раствором (Закон Рауля):

Относительное понижение давления насыщенного пара над раствором прямо пропорционально мольной доле растворенного вещества: где -давление насыщенного пара над чистым растворителем; Р_А-давление насыщенного пара растворителя над раствором; N_B- мольная доля растворенного вещества: 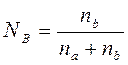, где n_a, n_b – число молей растворителя (а) и растворенного вещества (b).

Набольшее практическое значение получили I, II следствие закона Рауля.

I следствие закона Рауля: Повышение температуры кипения раствора прямо пропорционально молярной концентрации растворенного вещества: Dtкип = Kэб^.Сm , где Dtкип = t кип _р-ра – t кип н₂o, ⁰С ; Kэб – эбулиоскопическая константа растворителя (Kэб н₂о ); Сm- моляльная концентрация растворенного вещества, моль/1000г растворителя.

II следствие закона Рауля: Понижение температуры замерзания раствора прямо пропорционально молярной концентрации растворенного вещества: Dtзам =Kкр^.Сm , где Dt= t зам.н₂о – t зам _р-ра, ⁰С; Kкр - криоскопическая константа растворителя (Ккр н₂о =1,86); Сm- моляльная концентрация растворенного вещества, моль/1000г растворителя.

Росм = См R T Dtкип = Кэб Cm Dtзам = Ккр Cm

ß

Коллигативные свойства для молекулярных растворов

Примечание: см. приложение 7 – «Криоскопические константы некоторых растворителей», приложение 8 – «Эбулиоскопические константы некоторых растворителей».

Эти уравнения справедливы только для растворов, в которых отсутствует взаимодействие частиц, т.е. для идеальных растворов. В реальных растворах имеют место межмолекулярные взаимодействия между молекулами вещества и растворителя, которые могут приводить либо к процессам диссоциации, либо к процессам ассоциации молекул. Диссоциация молекул вещества в водном растворе характерна для сильных электролитов. В результате диссоциации число частиц увеличивается.

Доля (i) образовавшихся частиц определяется как отношение общего числа частиц к первоначальному числу молекул. Она зависит от степени диссоциации электролита и от числа частиц, на которые распадается молекула:

i = (n -1)a + 1, i – получил название изотонический коэффициент, n – число частиц (ионов), на которые распадается молекула, a – степень диссоциации (в долях).

Росм = iСМ R Т Dt кип = i Кэб Сm Dtзам = i Ккр Сm

ß

Коллигативные свойства для растворов электролитов

Примеры расчетов температур кипения, замерзания, осмотического давления растворов различных концентраций

Пример 1. Вычислить температуру замерзания, кипения раствора этилового спирта с процентной концентрацией (w), равной 40 %.

Решение: Вычислим температуру замерзания раствора исходя из II следствия закона Рауля: Dtзам = Kкр^.Сm, однако для решения необходимо перейти от одного вида концентрации к другому:

w [m в-ва, г \ 100г р-ра] ® Сm[ n молей \ 1000 г р-ля ]

1. Перейдем от массы вещ-ва (m) к молям (n) через пропорцию:

1 моль С₂Н₅ОН содержит ------- 46 г

х моль //------//-------//-------//------40 г

или по формуле х(n) = 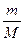= моль/100р-ра,

где m(с₂н₅он) = 40г, M(с₂н₅он) = 46г/моль

2. Перейдем от массы раствора к массе растворителя:

m р-ля = m р-ра - m в-ва = 100 – 40 = 60г р-ля

2. Через пропорцию выразим Сm :

0,87 молей С₂Н₅ОН содержит в 60 г растворителя

х (Сm) -//-----//-----//-----//------/- 1000 г

х (Сm) = 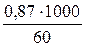= 14,5 молей/1000г р-ля

4. По формуле Dtзам = Kкр^.Сm найдем Dt: Dt = 1,86^.14,5 = 26,97 ⁰C

5. Dt = tзам н₂о – tзам_р-ра Þ tзам _р-ра = tзам н₂о – Dt = 0 - 26,97 = -26,97 ⁰C- температура замерзания 40 % раствора этилового спирта.

Вычислим температуру кипения раствора исходя из I следствия закона Рауля: Dtкип = Kэб^. Сm, Сm = 14,5 моль/1000р-ля (см. выше)

Из формулы найдем Dt: Dt = 0,516 ^. 14,5 = 7,48 ⁰C

Dt = tкип_р-ра – tкип н₂о Þ t_{кип р-ра} = tкип н₂о + Dtкип = 100+7,48=107,48 ⁰C- температура кипения 40% раствора этилового спирта.

Пример 2. Вычислить концентрацию физиологического раствора (NaCl) изотоничного с осмотическим давлением крови равное » 800 Кпа. Степень диссоциации NaCl принять за 90%.

Решение: Для растворов электролитов Росм(NaCl ) = i·См·R·T Þ

См = (1)

Условие изотоничности означает, что Росм(NaCl ) = Росм крови = 800 кПа,

i = (n-1)·a + 1= (2 - 1) ^·0,9 = 1,9

NaCl Û Na⁺+Cl^-, где n = 2, a = 0,9

Подставим найденные значения в формулу (1) См = 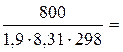0,17 моль/л – концентрация хлорида натрия, которая создает осмотическое давление 800 кПа.

Рекомендуемая литература: [1], с.225-230; [2], с.205-208.