Коэффициенты активности

Полярные соединения, прежде всего ионы, активно взаимодействуют между собой, вследствие чего по мере увеличения минерализации растет разница между концентрацией и активностью. Эту разницу характеризует коэффициент активности, который имеет размерность л·моль^-1 или кг·моль^-1. В практике термодинамических исследований принято использовать коэффициенты активности в единицах моляльности (кг·моль^-1), которые называют практическими.

Необходимость определения величин коэффициентов активности возникла в 20-ые годы прошлого столетия. Поиск методов их определения осуществлялся в двух основных направлениях: с позиции дальних электростатических и ближних кулоновых взаимодействий между ионами. Дальними электростатическими взаимодействиями в разбавленных растворах сильных электролитов занимались П.Э. Дебай и Э. Хюккель. В 1923 году они предложили теорию взаимодействия ионовв разбавленных растворах. Согласно этой теории электролиты в растворе диссоциированы полностью, а их ионы представляют собой жесткие неполяризуемые сферы с зарядами в центре, которые распределяются в однородной среде с высокой величиной диэлектрической постоянной так, что положительные ионы всегда окружены отрицательными и наоборот. При этом взаимодействие ионов в электронейтральной среде раствора определяется только электростатическими силами. Эти представления П.Э. Дебай и Э. Хюккель определяют содержание модели состояния идеального водного раствора (model ofstate ideal water solution).

В это же время на основе протонной теории Брёнстеда и Лауриусилиями Эдварда Арманда Гугенхейма (1901 – 1970) и Джон Н. Скэтчарда (1892-1973 ) формируется теория индивидуального взаимодействия ионов (specific ion interaction theory). В основе этой теории лежат представления о ближних взаимодействиях между отдельными ионами, которые измеряются величинами коэффициентов взаимодействия (interaction coefficients). Эта теория впоследствие легла в основу формирования модели состояния реального водного раствора (model ofstate real water solution).

Модель состояния идеального водного раствора П.Э. Дебая и Э. Хюккеля позволила построить относительно простое уравнение состояния идеального раствора электролитов, которое называют уравнением Дебая-Хюккеля (Debye–Hückel equation) . В первом приближении это уравнение имеет вид:

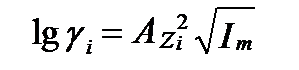, (II‑67)

где A - константа, которая характеризуют свойства растворителя и зависит только от температуры; z_i - заряд иона; I_m - ионная сила (ионность) (ionic strength) раствора.

Это выражение известно как предельный закон Дебая (Debye-Huckel limiting law), а коэффициент A называют его предельным коэффициентом (marginal coefficient)или коэффициентом предельного закона Дебая. Его величина определяется уравнением:

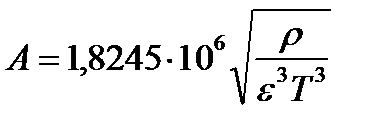. (II‑68)

Здесь T – абсолютная температура, а r и e - соответственно плотность растворителя (в общем случае раствора) и его диэлектрическая проницаемостьпри температуре T. Эта константа имеет размерность кг^0,5×моль^-0,5, а её величины приведены в таблице II-4.

Большое значение в этом уравнении первого приближения имеет величина I_m, которая представляет собой суммарную ионную силуили ионность раствора. Она была введена Г.Н. Льюисом и Мерле Рендаллом (1888-1950), чтобы охарактеризовать интенсивность электрического поля раствора и степень его отклонения от идеального состояния. Величина ионной силы пропорциональна сумме концентраций ионов, умноженных на квадрат их заряда:

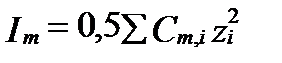, (II‑69)

где C_mi - моляльность иона в воде, z_i - его заряд. Например, в растворе NaCl, где присутствуют только однозарядные ионы Na⁺ и Cl^-, ионная сила будет равна:

I_NaCl = 0,5(z_Na²·C_NaCl + z_Cl²·C_NaCl) = C_NaCl,

а в растворе Na₂CO₃ получим:

I_Na2CO3 = 0,5(z_Na²·2C _Na2CO3 + z_CO3²·C _Na2CO3) = 3C _Na2CO3.

Поэтому в растворе только NaCl ионная сила равна концентрации соли, а в сложных растворах она, как правило, заметно выше общей минерализации. Ионная сила может быть представлена в единицах молярности или моляльности. Как правило, используют ионную силу в единицах моляльности. Для пересчета ионной силы раствора из молярной формы в мо­ляльную можно воспользоваться уравнением:

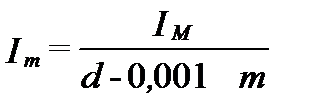, (II‑70)

где I_m и I_M – ионные силы моляльная и молярная, соотвественно, d - плотность водного раствора, m - его минерализация. Как видно из этого уравнения, для пресных вод разница между молярной и моляльной величинами ионной силы не велика, и ею иногда пренебрегают. Но эта ошибка заметно увеличивается с ростом минерализации и температуры, достигая при при 300^оС приблизительно 15%.

Рисунок II-7. Ионная сила разных природных вод (DM Sherman, University of Bristol).

Кроме того, состав воды, как уже отмечалось, может быть аналитическим и истинным (реальным). В связи с этим и ионная сила может быть стехиометрической и истинной. Стехиометрическая ионная сила (stoichiometric ionic strength)представляет собой величину рассчитанную по содержанию в растворе полностью диссоциированных ионов аналитического состава. Истинная ионная сила (true ionic strength)характеризуется величиной, полуенной с учетом процесса комплексообразования, т.е. реального состава раствора.

Уравнение (II-67) учитывает только удаленные электростатические взаимодействия между ионами, и поэтому работает при очень низких концентрациях, при I_m менее 0,01 (концентрации менее 10^-2 моль·кг^-1) .

С увеличением минерализации необходимо учитывать размеры ионов, а точнее возможное минимальное расстояние между ними. Уравнение Дебая-Хюккеля, которое это учитывает, рассматривается как уравнение второго приближения и имеет вид

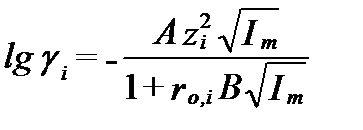, (II‑71)

где B – вторая константы, которые характеризуют свойства растворителя и зависят только от давления и температуры; а r_o,i- некоторая величина, которая зависит от эффективного диаметра отдельного иона i.

Константа B может быть рассчитана с помощью уравнения:

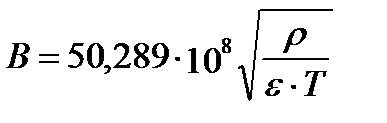, (II‑72)

и имеет размерность кг^0,5×моль^-0,5×см^-1. Её величины так же приведены в таблице II-4.

Рисунок II-8. Константы A и B уравнения Дебая-Хюккеля в моляльной шкале концентраций, рассчитанные по уравнениям II-68 и II-72 (Физическая химия под ред. Н.К. Краснова , 2001)

T, оС	ε	А	В ´10-8
	87,740	0,4917	0,3248
	85,763	0,4952	0,3256
	83,832	0,4988	0,3264
	81,945	0,5026	0,3271
	80,103	0,5066	0,3279
	78,303	0,5107	0,3287
	76,546	0,5150	0,3294
	74,823	0,5196	0,3302
	73,151	0,5242	0,3310
	71,511	0,5291	0,3318
	69,910	0,5341	0,3326
	68,344	0,5393	0,3334
	66,813	0,5443	0,3342
	63,855	0,5562	0,3359
	61,027	0,5685	0,3377
	53,317	0,5816	0,3395
	55,720	0,5958	0,3414

Наиболее уязвимой в этом уравнении является величина r_o,i (Табл. II-5). П.Э. Дебай и Э. Хюккель определили ее, как среднее расстояние, на которое ионы способны приблизиться друг к другу. Эту величину связывают с диаметром гидратированного иона и определяют экспериментальным путем, подбирая её так, чтобы рассчитанные по уравнению (II-67) коэффициенты активности совпадали с экспериментальными. Уязвимость этой величины, кроме того обусловлена ее зависимостью от температуры. В случае раствора NaCl она может меняться от 3×10^-8 до 4×10^{-8 см.}

Рисунок II-9. Величины r_o,i отдельных ионов в водных растворах при 25^оС (Гаррелс Р.М., Крайст Ч.Л., 1965).

ro,i´108	ионы
2,5	NH4+, Ag+, Rb+, Cs+, Tl+
	CNS–, CNO–, ClO4–, K+, Cl–, Br–, I–, CN–, NO2–, NO3 –
3,5	OH–, F–, HS–, BrO3–, IO4–, MnO4–
4-4,5	Na+, SO42–, HSO3–, HCO3–, HPO42–, H2PO4–, PO43–, Fe(CN)63–, Hg22–, SeO42–, CrO43 –
4,5	CO32–, Pb2+, SO32–, MoO42–
	Fe(CN)64-, Sr2+, Ba2+, Cd2+, Hg2+, S2–, Co32–, Ra2+, WO42–
	Ca2+, Cu2+, Zn2+, Sn2+, Mn2+, Fe2+, Ni2+, Co2+, Li+
	Mg2+, Be2+
	H+, Al3+, Fe3+, Cr3+,трехвалентные редкоземельные
	Th4+, Sn4+, Zr4+, Ce4+

Из-за несовершенства теории Дебая-Хюккеля и неопределенности величины r_o,i коэффициенты активности, рассчитанные по этой методике для растворов повышенных температур и давлений, даже при умеренной ионной силе (от 0,1 до 0,2) имеют точность только в пределах порядка величины. Поэтому уравнение Дебая-Гюккеля второго приближения используется только для пресных и солоноватых вод с I_m не более 0,2-0,5 (минерализация менее 0,1 моль·кг^-1) в условиях невысоких температур и давлений.

Пример 6: Имеем воду, содержащую Ca²⁺ 0,00584 M/кг, Mg²⁺ 0,0016 M/кг, HCO₃^- 0,00475 M/кг и SO₄^2- 0,00518 M/кг. Температура воды 25^оС.

I = 0,5(0,00584×2²+0,0016×2²+0,00475×1²+0,00518×2²) = 0,0276

Тогда в случае кальция A=0,5085, B=0,3281, r_o=6. Рассчитываем коэффициент активности:

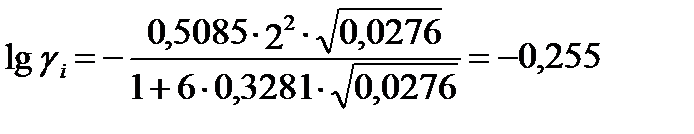; g_i = 0,556

Затем определяем величину активности кальция:

a_i= g_i× C_i = 0,556×0,00584=0,00325

С повышением минерализации разность между истинным коэффициентом активности и рассчитанным по уравнению (II-71) растёт. Эту разность можно выразить величиной:

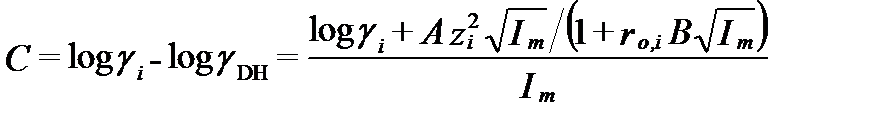, ( II‑73)

где γ_DH – коэффициент активности, рассчитанный по уравнению Дебая-Хюккеля второго приближения (II-71).

С учетом этой поправки получим уравнение третьего приближения:

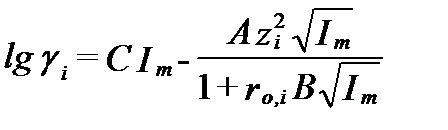, ( II‑74)

где слагаемое CI_m характеризует ошибку уравнения (II-71), вызванную ростом минерализации. Это слагаемое иногда называют функцией отклонения (deviation function). Для нейтральных компонентов раствора (z_i=0 ) второе слагаемое этого уравнения равно 0, и коэффициент активности опредляется только функцией отклонения. Традиционно считается, что неполярные растворенные соединения типа (H₄SiO₄)⁰ или (CaSO₄)⁰ ведут себя пассивно и имеют коэффициент активностиравный 1 даже в минерализованных водах. Поэтому последующие модифиции уравнение Дебая-Гюккеля, с целью сделать его пригодным для реальных растворов электролитов, касаются, в основном, взаимодействия ионов.

В условиях близких к стандартным чаще используется уравнение С.В. Дэвиса, опубликованное им в 1962 году (Davies, C. W., 1962). Он предлжил использовать в качестве функции отклонения произведение 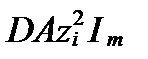, где D равно 0,2 или 0,3. Кроме того, он исключил в знаменателе произведение 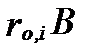, так как оно при 25^oC близко к 1. В итоге уравнение Дэвиса (Davies Equation) для 25^oC приобело вид:

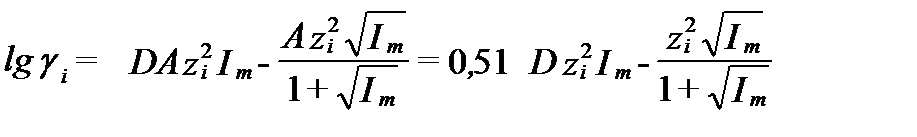. ( II‑75)

Эти дополнения не имеют теоретического обоснования, а новое уровнение игнорирует размеры ионов и даёт одинаковые значения γ_j при одинаковых зарядах. Как видно на рис. II-5, результаты уравнения Дэвиса убывают с ростом величины I_m, как и у уравнения Дебая-Хукеля второго приближения только до ионной силы около 0,1 моль·кг^-1, а затем начинает увеличиваться. При умеренной и высокой ионной силе это уравнение для расчета коэффициента активности микроконцентраций не рекомендуется Уравнение Девиса дает достаточно точные результаты при ионной силе до 0,5 моль·кг^-1. Его удобно использовать в геохимических моделях в стандартных условиях.

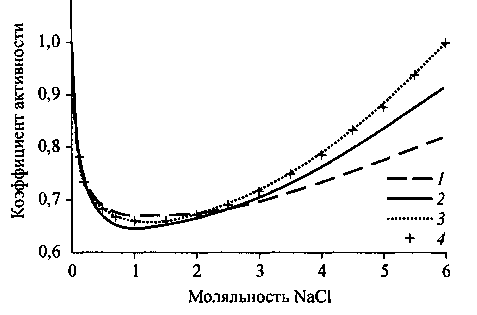Рисунок II-10. Зависимости средних коэффициентов активности ионов Na+ и Cl- от концентрации NaCl при их вычислении по уравнениям: 1- Дебая—Хюккеля (II-74), 2-Бронстеда-Гуггенхейма-Скэтчарда (II-76) и 3- Питцера (II-77).4- эксперименталь­ные значения. (Геологическая эволюция …, 2005)

Последующие усовершенствования методов расчета коэффициентов активности для минерализованных вод связаны с детализацией и усовершенствованием представлений о взаимодействии расворенных в воде компонентов. Совершенствовались представления о состояния водного раствора, менялись его модели, менялась методика расчета коэффициента активности. При этом можно выделить две основные тенденции в формировании моделей состояния водных растворов. Одна из них направлена на исследование состояния водных растворов в приповерхностных условиях, где температура меняется в ограниченном интервале, избыточное давление почти отсутствует, и его влиянием практически пренебрегают. Вторая направлена на исследование состояния водных растворов больших глубин, где как температура, так и давление меняются в очень широком диапазоне, и их влияние учитывается.

Формирование первого направления тесно связано с работами Й. Н. Бронстеда Е. А. Гугенхейма и Д. Н. Скэтчарда (Scatchard G., 1976 ), которые в 20-30 ые годы прошлого столетия предложили теорию индивидуальных взаимодействий ионов (specific ion interaction theory). На основе этой теории сформировалась модель Бронстеда-Гуггенхейма-Скэтчарда (Bronsted-Guggenheim-Scatchard model ) или модель теории индивидуальных взаимодействий (specific ion interaction Theory - SIT) . Эта модель объединяет взаимодействие электростатических и кулоновых сил компонентов в растворе с учетом их идивидуальных свойств. В её основу были положены представления о широком разнообразии взаимодействий компонентов раствора между собой, которое характеризуется величиной некоторого коэффициента взаимодействия (interaction coefficients). Согласно этой модели уравнение определения коэффийиента активности приобрело вид:

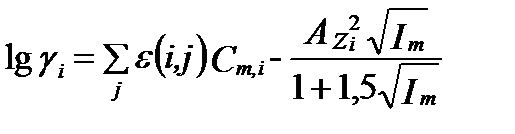, (II‑76)

где ε(i,j) - коэффициенты взаимодействия (interaction coefficients ) иона i со всеми другими ионами j с противоположным знаком заряда. В этом уравненииБронстеда-Гуггенхейма-Скэтчарда (Bronsted-Guggenheim-Scatchard model )первое слагаемое (функция отклонения) характеризует влияние ближних сил взаимодействия ионов, и базируется на теории специфического взаимодействия ионов. Второе слагаемое (уравнение Дебая-Хюккеля)характеризует влияние дальних, электростатических сил взимодействия ионов. Однако это уравнение учитывает взаимодействие только ионов противоположного заряда. Оно не учитывало взаимодействия ни нейтральных соединений, ни ионов одного знака заряда, ни трех ионов сразу, роль которых увеличивалась с ростом минерализации.

В 1973 году Кеннет Сенборн Питцер (1914-1997) предпринял попытку учесть эти взаимодействия в составе раствора. Он включил бинарные взаимодействия: катион-анион, анион-анион, катион-катион, катион-нейтральный компонент, анион-нейтральный компонент, нейтральный компонент-нейтральный компонент и тройные взаимодействия: катион-катион-анион, анион-анион-катион и т.д. Для этого он разложил первый член уравнения (II-76) в ряд слагаемых с вириальными коэффициентами (Pitzer, K. S., 1973). Каждое из этих слагаемых характеризует какой-либо один тип взаимодействия. Его модель более детального учета взаимодействия компонентов водного раствора иногда называют моделью Питцера (Pitzer model). Согласно этой модели уравнение (II-76) получило вид вириального уравнения состояния раствора, или уравнения Питцерас вириальными коэффициентами:

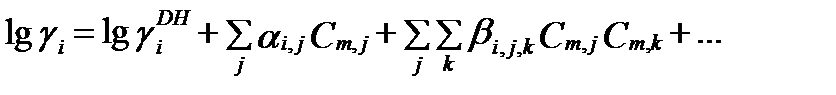(II‑77)

где 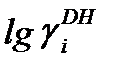- несколько измененный коэффициент активности Дебая-Хюккеля, зависимый только от величины ионной силы, α_i,j и β_i,j,k – коэфициенты каждого отдельного вида взаимодействия, которые называюткоэффициентами взаимодействия второго и третьего порядка, и которые зависят от ионной силы и температуры. Параметры бинарных и тройных взаимодействий основных ионов, определенные экспериментально для достаточно широкого интервала температур, можно найти в опубликованной и справочной литературе. Полуэмпирическая модель плотных электролитов Питцера позволяет моделировать состав разных водно-солевых систем в широком диапазоне температур с достаточной точностью.

Формирование втрого направления тесно связано с исследованием гидротермальных растворов и с именем Гарольда Хельгесон (1931 –2007). На первом этапе 1967 году Г.Хельгесон распространил действие коэффициентов A и B в уравнении Дебая-Хюккеля до 300^oC. В этом диапазоне температур влияние давления не существенно. Поэтому Г. Хельгесон ограничился только незначительной модернизацией функции отклонения для учета влияния ионной силы (Helgeson, 1969). В американскую литературу это уравнение вошло под названием уравнение B с точкой (B-dot Equation) , так как в уравнении (II-74) вместо коэффициента C использовалось 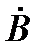(B с точкой). Величина этого коэффициента с температурой растет, достигает максимума около 150-200 ^oC, а затем резко падает (См. таблицу II-6). Этот коэффициент является эмпирическим по раствору NaCl. Поэтому для растворов, где преобладают компоненты Na+ и Cl^-, он пригоден при минерализации до 3 моль·кг^-1, а для других ионов при минерализации до 1 моль·кг^-1.

Рисунок II-11. Константы A, B и C уравнения (II-74 или уравнения В с точкой) в моляльной шкале концентраций, рассчитанные по уравнениям II-68 и II-72 (Helgeson, 1969)

T, оС	А	В ´10-8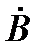
	0,5095	0,3284	0,041
	0,5354	0,3329	0,043
	0,6019	0,3425	0,046
	0,6915	0,3536	0,047
	0,8127	0,3659	0,047
	0,9907	0,3807	0,034
	1,0905	0,3879	0,015
	1,2979	0,4010	0,0

Стремясь расширить диапазон геохимического прогноза до условий больших глубин (до температуры 600^oC и давления 5000 атм) Г.Хельгесон с соавторами вынужден был в 1974-1981 годы существенно изменить свои представления. Эти изменения касались в основном влияния давления и ионной силы. В 1981 году ими была предложена новая модель термодинамического состояния растворов электролитов в диапазоне высоких температур и давлений, которую назвали по инициалам авторов моделью состояния Хелгесона-Киркхэма-Флауэрса (ХKФ) (model HRF) (Helgeson H.C. et al., 1981). Наконец, в 1988 году тот же коллектив с Г.Хельгесон во главе предложил модифицированную модеь (Tanger J.C., Helgeson H.C., 1988), которая в настоящее время широко используется для исследования гидротермальных и метаморфических процессов, как исправленная модельХелгесона-Киркхэма-Флауэрса (ХKФ) (revised model HRF) . В основе этих моделей лежит допущение, что все стандартные парциальные моляльные термодинамические свойства растворенных в воде компонентов (свободная энтальпия, энтропия, объем,теплоемкость и т.д.) представляют собой сумму двух слагаемых. Одно из них отражает влияние внутренних свойств не связанных с гидратацией. Второе слагаемое характеризует влияние гидратации, вызванное электростатическим взаимодействием иона с диполями H₂O. Благодаря этому допущению эта модель учитывает не только взаимодействия растворенных компонентов между собой, но и влияние этих компонентовн на структуру и свойства растворителя. Она позволяет моделировать геохимические процессы в условиях до 1000^oC температуры, до 5000 ат давления и до 4-6 моль·кг^-1 инной силы.

Активность H₂O

Активность влаги (activity of moisture)в составе пресных вод близка к 1, и принимается равной этой величине. Но по мере роста минерализации величина этой активности уменьшается, так как она определяется концентрацией свободной молекулы H₂O, которая не находится под влиянием сил гидратации. Активность влаги можно выразить через величины ее фугитивности:

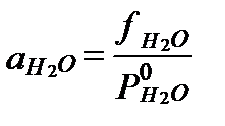, (II‑78)

где 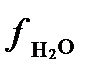- фугитивность пара H₂O над раствором при данной температуре, а 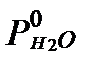- давление насыщенного пара чистой воды в стандартных условиях. Поэтому активность влаги можно оценить по величине фугитивности или парциального давления H₂O над разбавленным раствором при заданной.

В настоящее время активности влаги определяется путем экспериментального измерения парциального давления пара H₂O над раствором, или осматического коэффициента j. Активность влагив случае одного растворенного электролита связана с величиной осматического коэффициента уравнением:

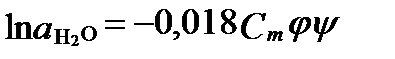, (II‑79)

где C_m- моляльность раствора; y - суммарное число ионов, на которое диссоциирует растворённый электролит. По расчетам Г.А. Соломина (Крайнов С.Р., Соломин Г.А., 1990) при увеличении минерализации от 1 до 600 г/л активность влаги уменьшается от 1 до 0,3. Это вызвано гидратацией растворенных компонентов и уменьшением концентрации свободных молекул H₂O.

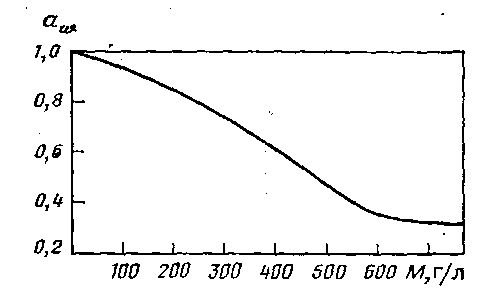Рисунок II-12. Изменение активности влаги в подземных водах в зави­симости от их минерализации (Крайнов С.Р., Соломин Г.А., 1990)

Закон действия масс

Предположим, что смешались два разных по составу раствора. Вследствие этого образовался новый раствор, состав которого можно определить с помощью уравнений II-1 и II-2. Если новый раствор оказался неравновесным, его компоненты будут самопроиз­вольно взаимодействовать между собой, пока не достигнут нового равновесного состава, с более низким содержанием свободной энтальпии. Компоненты, содержание которых при этом взаимодействии не менялось, не влияли на свободную энтальпию раствора, и их можно игнорировать. Интерес представляют только те компоненты, которые изменили свое содержание и, следовательно, химический потенциал. Концентрации одних из них уменьшились, а у других увеличилось. Компоненты, содержание которых уменьшилось, называют реагентами (reactants), и их величины dN_i пишут слева от знака равенства. Компоненты, содержание которых увеличилось, назовают продуктами (products), и их величины dN пишут справа от знака равенства. В итоге получим уравнение:

dN₁+ dN₂+...+ dN_k → dN_k+1 + dN_k+2...+ dN_k+m, (II‑86)

которое характеризует процесс изменения состава раствора на его пути к равновесному состоянию.

Изменение концентрации любого компонента на число молей dξ связано с некоторой полезной работой, величина которой при постоянстве давления и температуры может быть выражена, с помощью уравнения II-76. Эта работа в единицах свободной энтальпии будет равна:

.

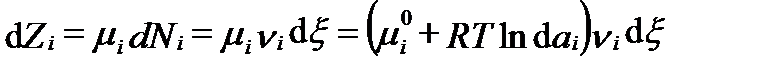Суммируя всю свободную энтальпию реагентов (левой половины уравнений реакций) получим :

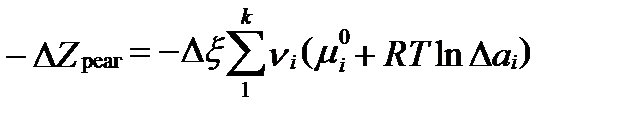, (II‑87)

Суммируя всю свободную энтальпию продуктов (правой половины уравнений реакций) получим :

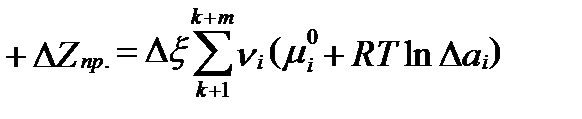. (II‑88)

Наконец, суммируя эти два слагаемые и полагая, что Δa_i = a_i, получим общее изменение свободной энтальпии в процессе химической реакции:

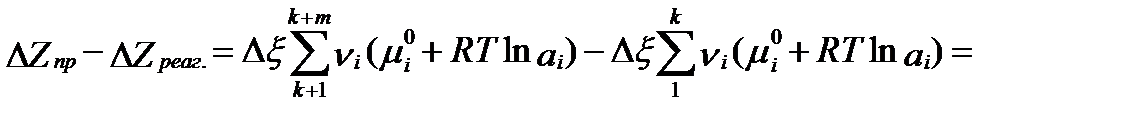
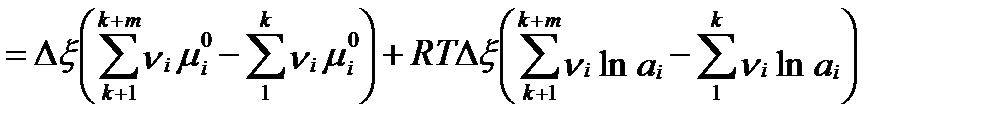. (II‑89)

Если принять стехиометрические коэффициенты ν_i у продуктов реакций положительными, а у реагентов отрицательными, это уравнение можно существенно упростить. Тогда первая разность в скобках уравнения II-84 примет вид:

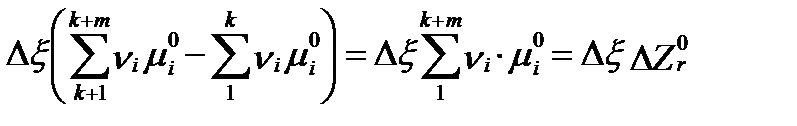. (II‑90)

Величина этой разности характеризует изменение свободной энтальпии по ходу реакции в стандартных условиях, когда активности всех участвующих компонентов равны 1.

Вторая разность в скобках уравнения II-84 также упростится и примет вид:

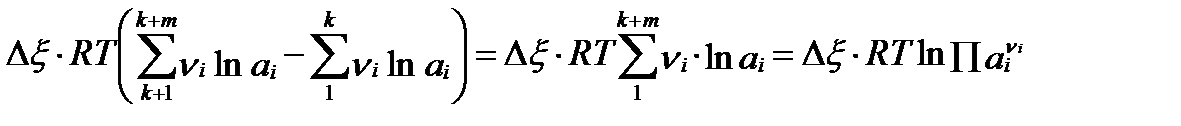. (II‑91)

Символ Π в этом уравнении обозначает оператор произведения. Само уравнение характеризует отклонение общего изменения свободной энтальпии от величины 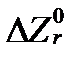, вследствие того, что активности компонентов не равны 1. Произведение 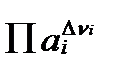характеризует произведение величин активности всех компонентов, участвующих в реакции, в степени численно равной их стехиометрическим коэффициентам, положительным у продуктов, и отрицательных у реагентов.Оно играет важную роль в термодинамике химических процессов и называется произведением активностей (activity product) или квотантом (quotient)реакции. Это произведениевпредь будет обозначаться для краткости символом:

.

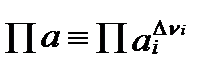Таким образом, полное изменение свободной энтальпии в процессе одной химической реакции на пути релаксации приобретет упрощенный вид:

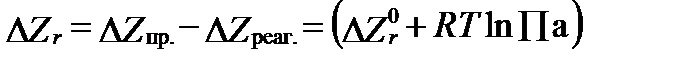. (II‑92)

Так как при самопроизвольной необратимой реакции свободная энтальпия системы только уменьшается, DZ_r имеет отрицательное значение,DZ_пр. < DZ_реаг., и

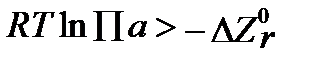. (II‑93)

По мере приближения реакции к равновесию величина DZ_r стремится к 0. Когда химическое равновесие достигнуто, и реакция становится обратимой, соблюдается равенство:

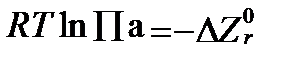. (II‑94)

Отсюда следует, что - 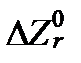и есть та минимальная свободная энтальпия, при которой наступает химическое равновесие реакции в стандартных условиях.

Таким образом, в условиях релаксации состав раствора меняется так, чтобы иметь минимальную величину свободной энтальпии свойственную данным условиям. Это изменение раствора можно проследить с помощью величины произведения активностей. Когда реакция достигает равновесия, произведение активности имеет только одно конкретное значение, которое зависит только от температуры и давления. Это значение произведения активностей в условиях химического равновесия при стандартных условиях называют стандартнойконстантой равновесия (standard equilibrium constant)реакций. Она определяется уравнением:

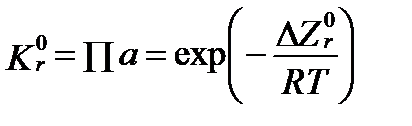. (II‑95)

Это уравнение является термодинамическим выражением закон действия масс (law of mass action)или действующих масс. Необходимо иметь в виду, что этот закон имеет две ипостаси: кинетическую и термодинамическую. Первоначально он был открыт норвежцами Като Максимилан Гульдберг (1836-1902) и Петер Вааге (1833-1900) в 1863-67 годах на основе кинетических исследований в разбавленных растворах. Они экспериментально доказали, что скорость реакций пропорциональна произведению "масс реагентов в реакции", то есть "действующих масс", откуда и возникло название рассматриваемого закона. В основе этой кинетической интерпретации закона лежит количество взаимодействующих компонентов, число их столкновений. Термодинамическое обоснование закона было дано лишь в 1885 году Якубом Генрикусом Вант-Гоффом (1852-1911). В основе этой термодинамической интерпретации закона лежит энергия взаимодействующих связей. Согласно этому закону при химическом равновесии произведение активностей взаимодействующих соединений имеет строго определённое значение, названное константой равновесия реакции. Именно в этом случае величина свободной энтальпии раствора остается минимальной и постоянной для данной температуры и давления.