Графическое изображение экспериментальных данных
Наиболее выразительная, информативная и удобная форма представления экспериментальных данных – графическая. При этом чаще используется прямоугольная система координат. По оси абсцисс откладываются значения независимой переменной, а по оси ординат – значение функции этой переменной.
График строят на миллиметровой бумаге. Построение графика начинают с выбора его размеров и масштаба координатных осей.
Вначале по наименьшему и наибольшему значениям откладываемых по осям величин находят интервалы их изменения, затем подбирают площадь, достаточную для размещения этих интервалов. Очевидно, что в целях сокращения неиспользуемой площади графика не следует начинать ось с нуля, когда откладываемая величина известна не с нулевого значения (рис. 2.1).
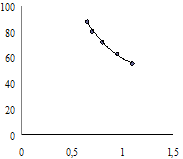 а а | 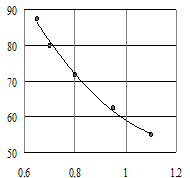 б б |
Рис. 2.1. Построение графиков: а – неправильное; б – правильное
Масштаб подбирают удобным для работы, т.е. выбирают удобную единицу длины по оси графика. Например, 1см по оси соответствует 0,2; 0,5; 1; 2,5 или 10 единицам, но не 0,17; 0,54; 1,3; 2,48 и т.д.
На обе оси графика наносят равномерные цифровые шкалы. Их оцифровка также должна выполняться удобными для работы цифрами и проставляться не слишком часто и не слишком редко. В конце каждой оси должны находиться условное обозначение откладываемой величины и ее единица, например: С, %.
При отсутствии общепринятого обозначения вдоль оси пишут название и единицу этой величины. Если измеряемые величины выражаются многоразрядными цифрами, то их записывают через множитель 10±n, который ставят рядом с условным обозначением или названием этих величин, например: d·10–6.
Экспериментальные точки наносят на поле графика без описания их координат на поле и на осях. Координаты точек определяются оцифровкой шкал и положением точек на графике. Во избежание путаницы в экспериментальных точках при нанесении на один график нескольких зависимостей, а также путаницы за счет случайно или неверно нанесенных точек и помарок каждую действительную точку обводят кружком, треугольником или другой фигуркой.
По проставленным точкам строят линию – функциональную зависимость. Так как случайные ошибки неизбежны, точки могут располагаться на графике с некоторым разбросом. Поэтому линию проводят так, чтобы она проходила как можно ближе ко всем точкам, а точки располагались по возможности равномерно и симметрично около линии. Построение графика есть графическое усреднение экспериментальных данных, поэтому не следует вести линию непосредственно через отклоняющиеся точки или очень близко к ним. Это приведет к появлению неровностей на линии, она перестанет служить средством усреднения. Обычно прямые строят с помощью линейки, а плавные кривые – с помощью лекал.
С помощью графика можно найти значения функции и аргумента, которые непосредственно опытом не определялись. Для этого достаточно любую точку на кривой спроектировать на оси координат. Если значение аргумента находится внутри изученного интервала, то операцию нахождения функции при данном промежуточном значении аргумента называют графической интерполяцией. Если же значение аргумента находится за пределами изученного интервала, определение функции проводят путем продолжения кривой за пределы интервала. Такая операция называется графической экстраполяцией.
Типичной ошибкой в построении графиков является нанесение экспериментальных значений величин на оси ординат. Это затрудняет проведение интерполяции и экстраполяции. Для быстрого и точного выполнения указанных операций необходимо на оси координат нанести равномерные шкалы с ценой деления, соответствующей округленному значению чисел.
На полях и осях графика не должно быть лишних надписей и цифровых сносок. Подпись к рисунку должна содержать номер рисунка, название зависимости и расшифровку условных обозначений графика. Рассмотрим пример правильного и неправильного оформления графика (рис. 2.2).
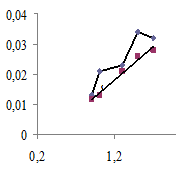 а а | 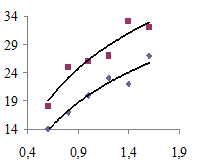 б б |
Рис. 2.2. Примеры оформления графика:
а – неправильное; б – правильное
При оформлении графика допущены следующие ошибки:
1. Неверный выбор начала координат, наличие неиспользованной площади графика.
2. Неудачный выбор соотношения осевых масштабов, в результате чего наклон кривых очень мал.
3. Отсутствие масштабной единицы на оси ординат, неравномерная разметка оси, неудобная громоздкая и нерегулярная оцифровка.
4. Нерегулярная и слишком тесная оцифровка оси абсцисс.
5. Отсутствие обозначения и единицы физической величины на оси абсцисс и ординат.
6. Неверно проведена верхняя линия графика: вместо ломаной следовало провести плавную кривую.
7. Неверно проведена нижняя линия графика: слева точки оказались под линией, а справа – над ней, тогда как на всем протяжении линия должна проходить между точками.
