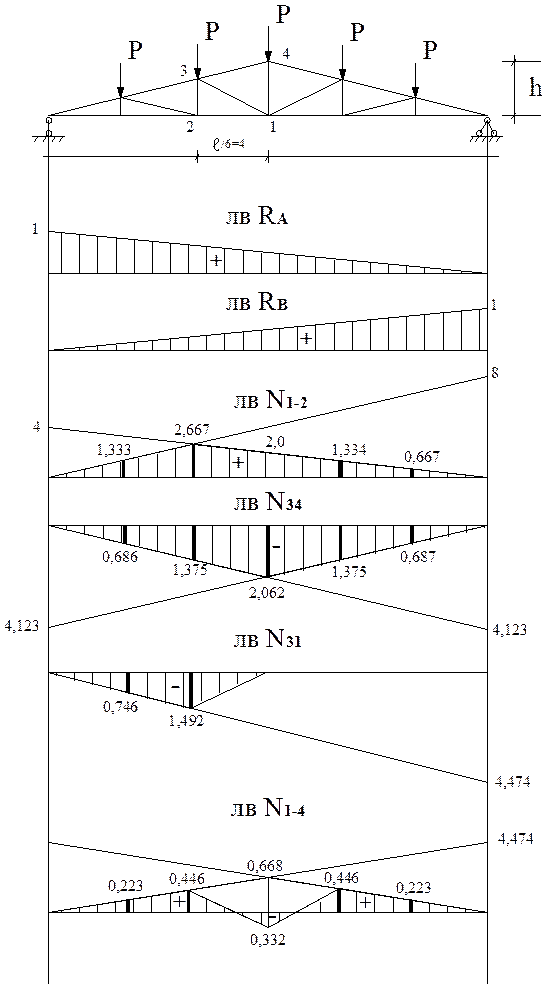Пример расчета простой плоской статически
Определимой фермы.
Для фермы с выбранными по шифру из таблицы размерами и нагрузкой требуется:
а) определить (аналитически) усилия в стержнях заданной панели, включая правую стойку (4 стержня);
б) построить линии влияния усилий в тех же стержнях;
в) по линиям влияния подсчитать значения усилий от заданной нагрузки и сравнить их со значениями, полученными аналитически;
Исходные данные:
№ панели (считая слева) =3 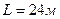 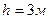 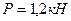 № схемы 1 № схемы 1 | 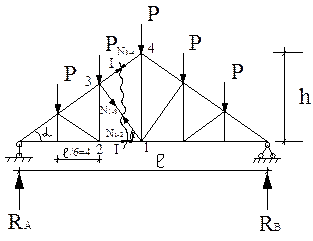 |
Решение:
1. Определение опорных реакций от действия заданной постоянной нагрузки
а) определяем опорные реакции, для этого составляем уравнения стати-ческого равновесия, рассматриваем сумму моментов всех сил, приложенных к ферме, относительно опорных точек:
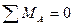
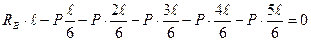
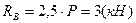
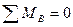
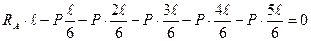
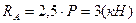
б) для проверки найденных опорных реакций составим уравнение ста-ического равновесия, а именно – сумма проекций всех сил, приложенных к ферме, на вертикальную ось должна равняться нулю:
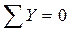
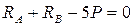
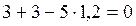
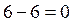
2. Определение усилий в стержнях указанной панели:
а) усилие в стержне нижнего пояса 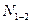 определяем методом сечений. Проведём сечение I-I.
определяем методом сечений. Проведём сечение I-I.
Составляем уравнение суммы моментов всех сил, приложенных слева от сечения относительно моментной точки, в качестве моментной точки исполь-зуем точку 3 , в которой сходятся оси двух других из трех рассеченных стерж-ней, за исключением рассчитываемого:
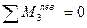
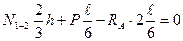
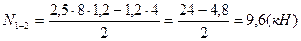
б) усилие в стержне верхнего пояса 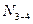 определяем методом сечений. Воспользуемся тем же сечением I-I. Составляем уравнение суммы моментов всех сил, приложенных слева от сечения относительно моментной точки, в качестве моментной точки используем точку 1, в которой сходятся оси двух других из трех рассеченных стержней, за исключением рассчитываемого:
определяем методом сечений. Воспользуемся тем же сечением I-I. Составляем уравнение суммы моментов всех сил, приложенных слева от сечения относительно моментной точки, в качестве моментной точки используем точку 1, в которой сходятся оси двух других из трех рассеченных стержней, за исключением рассчитываемого:
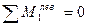
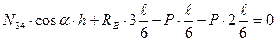
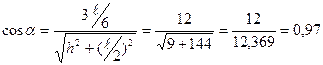 ;
;
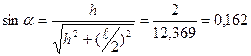
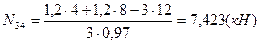
в) усилие в раскосе 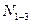 определяем методом сечений (сечение I-I). Сос-тавляем уравнение суммы моментов всех сил, приложенных слева от сечения относительно моментной точки А:
определяем методом сечений (сечение I-I). Сос-тавляем уравнение суммы моментов всех сил, приложенных слева от сечения относительно моментной точки А:
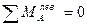
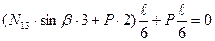
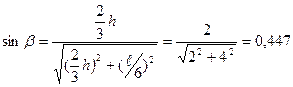
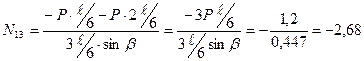
г) усилие в стойке 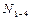 определяем методом вырезания узлов. Составляем уравнение статического равновесия – сумма проекций всех сил, приложенных к узлу 4 на вертикальную ось должна равняться нулю:
определяем методом вырезания узлов. Составляем уравнение статического равновесия – сумма проекций всех сил, приложенных к узлу 4 на вертикальную ось должна равняться нулю:
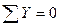 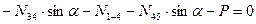 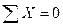 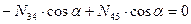 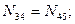 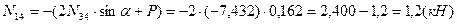 | 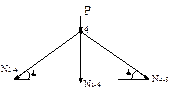 |
3.Построение линий влияния в стержнях фермы.
Линия влияния - это графическое изображение закона изменения како-го либо усилия в заданном сечении при движении по сооружению силы Р=1.
Что бы графически изобразить закон изменения усилия надо сначала выя-вить этот закон аналитически, при этом используются те же методы и способы, что и при аналитическом расчёте усилий в стержнях ферм на действие пос-тоянной нагрузки.
а) линию линия усилия в стержне нижнего пояса 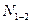 рассчитываем методом сечений. Составляем уравнение суммы моментов всех сил, прило-женных по одну сторону от сечения относительно моментной точки, в качестве моментной точки используем точку 3, в которой сходятся оси двух других из трех рассеченных стержней, за исключением рассчитываемого.
рассчитываем методом сечений. Составляем уравнение суммы моментов всех сил, прило-женных по одну сторону от сечения относительно моментной точки, в качестве моментной точки используем точку 3, в которой сходятся оси двух других из трех рассеченных стержней, за исключением рассчитываемого.
Если сила Р=1 находится слева от рассеченной панели:
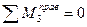 ;
; 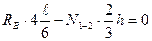
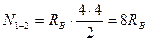
Если сила Р=1 находится справа от рассеченной панели
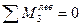 ;
; 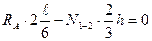
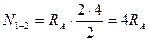
В пределах рассеченной панели строим передаточную линию.
а) линию влияния усилия в стержне верхнего пояса 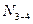 рассчитываем методом сечений. Составляем уравнение суммы моментов всех сил, приложен-ных по одну сторону от сечения относительно моментной точки, в качестве моментной точки используем точку 1, в которой сходятся оси двух других из трех рассеченных стержней, за исключением рассчитываемого.
рассчитываем методом сечений. Составляем уравнение суммы моментов всех сил, приложен-ных по одну сторону от сечения относительно моментной точки, в качестве моментной точки используем точку 1, в которой сходятся оси двух других из трех рассеченных стержней, за исключением рассчитываемого.
Если сила Р=1 находится слева от рассеченной панели

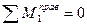 ;
; 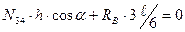
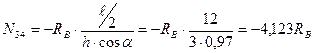
Если сила Р=1 находится справа от рассеченной панели
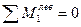
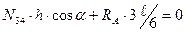
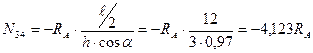
В пределах рассеченной панели строим передаточную линию.
а) линию влияния усилия в стержне раскоса 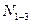 рассчитываем методом се-чений. Составляем уравнение суммы моментов всех сил, приложенных по одну сторону от сечения относительно моментной точки, в качестве моментной точ-ки используем точку А , в которой сходятся оси двух других из трех рас-сеченных стержней, за исключением рассчитываемого.
рассчитываем методом се-чений. Составляем уравнение суммы моментов всех сил, приложенных по одну сторону от сечения относительно моментной точки, в качестве моментной точ-ки используем точку А , в которой сходятся оси двух других из трех рас-сеченных стержней, за исключением рассчитываемого.
Если сила Р=1 находится слева от рассеченной панели
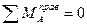
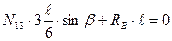
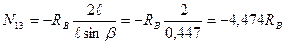
Если сила Р=1 находится справа от рассеченной панели
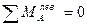
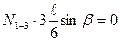
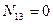
В пределах рассеченной панели строим передаточную линию.
г) линию влияния усилия в стойке 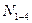 рассчитываем методом вырезания уз-лов. Составляем уравнение статического равновесия – сумма проекций всех сил, приложенных к узлу 4 на вертикальную ось должна равняться нулю, так как узел 4 принадлежит верхнему поясу, и сила Р=1 перемещается по верхнему поясу, то если сила Р=1 находиться вне узла 4:
рассчитываем методом вырезания уз-лов. Составляем уравнение статического равновесия – сумма проекций всех сил, приложенных к узлу 4 на вертикальную ось должна равняться нулю, так как узел 4 принадлежит верхнему поясу, и сила Р=1 перемещается по верхнему поясу, то если сила Р=1 находиться вне узла 4:
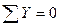
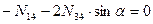
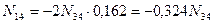
то если сила Р=1 находиться в узле 4 :
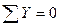
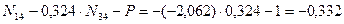
4. Определение значения усилий от постоянной нагрузки, для этого воспользуемся выражением:

 Ni =
Ni = 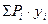
где Ni–усилие в рассматриваемом стержне, Pi – приложенная заданная сосредоточенная сила, yi- ордината линии влияния, расположенная под точкой приложения силы Pi. Ординаты линий влияния определяем из подобия треугольников, используя в качестве отправных характерные (базовые) ординаты линий влияния:
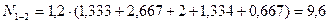 (кН)
(кН)
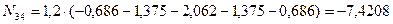 (кН)
(кН)
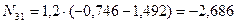 (кН)
(кН)
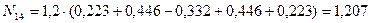 (кН)
(кН)