Уравнение Михаэлиса-Ментен

Важнейшим фактором, определяющим скорость ферментативной реакции, является концентрация реагирующих веществ, концентрация субстратов. Как было указано выше, фермент взаимодействует с субстратом с образованием фермент-субстратного комплекса. Затем фермент-субстратный комплекс распадается с образованием продукта реакции, а катализатор остается в исходном состоянии. Ниже приведено уравнение, отражающее процесс ферментативного катализа с образованием продукта реакции:

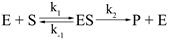
Как видно из этого уравнения, фермент Е взаимодействует с субстратом S с образованием фермент-субстратного комплекса ES. Этот процесс характеризуется константой скорости – k₁. Комплекс ES способен распадаться на исходные компоненты – Е и S с константой скорости k₋₁. Константа k₂ представляет собой константу скорости распада комплекса ES с образованием продукта реакции.

Вполне очевидно, что фермент-субстратный комплекс способен к обратимой диссоциации в соответствии с уравнением:

Исходя из закона действующих масс, скорость образования комплекса ES можно записать следующим образом:

,

где k₁ – константа скорости реакции образования комплекса ES.

Поскольку комплекс ES способен диссоциировать без образования продукта реакции скорость распада комплекса ES можно выразить уравнением:

,

где k₋₁ – константа скорости реакции распада комплекса ES.

При равенстве скоростей V₁ и V₂ получим выражение:

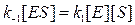
Разделив обе части уравнения на величину k₁, получим: [E][S] = k₋₁/k₁ [ES], где k₋₁/k₁ представляет собой величину называемую константой диссоциации – K_S.

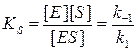
После соответствующего преобразования выражение приобретает вид:

В последнем уравнении величину [E] можно представить как [E₀]–[ES], что представляет собой концентрацию свободного фермента за вычетом концентрации фермента, связанного с субстратом [ES]. Величина [E₀] – общая концентрация фермента в начале реакции. Подставив в предыдущее уравнение вместо [E] – [E₀]–[ES] получим:

После преобразования последнего уравнения получаем:

Максимальная скорость ферментативной реакции достигается в ситуации, когда концентрация комплекса ES равна начальной концентрации фермента Е₀ т.е. [ES] = [E₀]. Таким образом, можно записать следующее выражение:

Поскольку из предыдущего выражения следует, что:

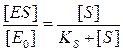
то получаем:

или

Последнее уравнение получило название уравнения Михаэлиса-Ментен. Графически зависимость между концентрацией субстрата и скоростью реакции отображает рис. 6.1. Из этого рисунка видно, что при низких концентрациях субстрата реакция характеризуется первым порядком, а при его высоких концентрациях становится реакцией нулевого порядка, когда скорость реакции становится постоянной величиной.

Следует, однако, помнить, что уравнение Михаэлиса-Ментен справедливо только для начального времени реакции, когда присутствует избыток субстрата и образуется небольшое количество продукта. Именно поэтому уравнение Михаэлиса-Ментен носит несколько ограниченный характер, поскольку оно учитывает только первую часть процесса и не учитывает его вторую стадию – влияние продукта реакции и его взаимодействие с ферментом. В связи с этим Холдейном и Бриггсом было предложено усовершенствованное выражение уравнения Михаэлиса-Ментен:

,

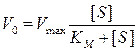где К_M – константа Михаэлиса, которая равна концентрации субстрата (выраженной в молях/литр), при которой скорость реакции составляет половину максимальной скорости. Численное значение константы Михаэлиса может быть выражено следующим образом:

Преобразованное Холдейном и Бриггсом уравнение Михаэлиса-Ментен, которое имеет вид

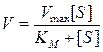
описывает поведение многих ферментов при измене­нии концентрации их субстратов. Используя это урав­нение можно рассмотреть несколько ситуаций, отражающих влияние [S] и К_M на начальную скорость фермента­тивной реакции:

1. Значение [S]намногоменьше величины К_M (рис. 6.1). В этом случае величину [S] в знаменателе можно опу­стить, и он будет практически равен величине К_M. Отношение двух постоянных величин – V_max и К_M, можно заменить новой константой К. Таким образом, имеем:

;

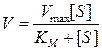( @ означает «примерно равно»).

Другими словами, когда концентрация субстрата значительно ниже величины К_M – начальная скорость реакции, V₀, пропорциональна концентрации субстрата [S];

2. Значение [S]намногобольше величины К_M (рис. 6.1). Тогда величиной К_M в знаменателе можно пренебречь, т.е.

;

Это означает, что при концентрации субстрата [S], намного превышающей К_M, начальная скорость V₀рав­на максимальной скорости – V_max;

3. Наконец, при равенстве величин [S] и К_M (рис. 6.1) в знаменателе уравнения Михаэлиса-Ментен получим удвоенное значение [S].

;

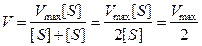
Это означает, что при концентрации субстрата, равной К_M, начальная скорость реакции V₀ составляет половину максимальной скорости – V_max.

Графическое определение константы Михаэлиса (К_m)

Графически константа Михаэлиса может быть представлена, как это показано на рис. 6.1. Однако в случае многих ферментов определение V_max и К_M непосредственно из графика зависимости V₀ от [S] (рис. 6.1) оказывается затруднено. Для большего удобства уравнение Михаэлиса-Ментен было преобразовано Лайнуивером и Берком в координатах двойных обратных величин:

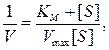
Правую часть уравнения представляют в виде суммы двух слагаемых:

Упростив уравнение, получаем:

Как можно видеть, это уравнение представляет собой уравнение прямой:

у = ах + b,

где у = 1/V₀ и х = 1/[S].

Если построить график зависимости у (т.е. 1/V₀) от х (т.е. 1/[S]), то длина отрезка b, отсекаемого на оси у, будет равна 1/V_max, а тангенс угла наклона – а равен величине K_M/V_max. Длину отрезка, отсекаемого на оси х (в области отрицательных значений), можно получить, приравняв к нулю. Тогда получим:

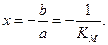
График уравнения Михаэлиса-Ментен в обрат­ных координатах называют графиком Лайнуивера-Берка (рис. 6.2). Используя его, величину K_M можно определить либо по наклону прямой и длине отрезка, отсекае­мого на оси у, либо по длине отрезка, отсекаемого в области отрицательных значений на оси х. Поско­льку [S] измеряют в молях/литр, K_M имеет ту же размерность. Скорость V₀ мо­жет быть выражена в любых единицах, поскольку K_M не зависит от [E]. ГрафикЛайнуивера-Берка позволяет определять K_M по отно­сительно небольшому числу точек, поэтому он часто используется для расчета этого параметра.

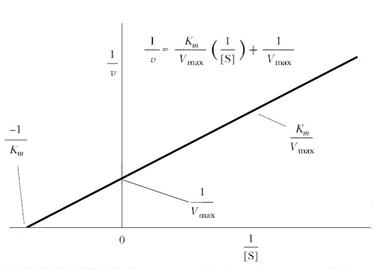
Рис. 6.2

График Лайнуивера-Берка в двойных обратных координатах (зависимость 1/V0 от 1/[S]), используемый для графического определения KM и Vmax.

Используя график Лайнуивера-Берка на прак­тике, при определении K_M, иногда сталкиваются с тем, что почти все точки оказываются в области низких кон­центраций субстрата. Это происходит в тех случаях, когда измерения проводят через равные интервалы [S]. Чтобы этого избежать, измерения следует прово­дить при таких значениях [S], которые соответ­ствуют равным интервалам на оси х в обратных ве­личинах.

Еще одним вариантом линеаризации зависимости скорости ферментативной реакции от концентрации субстрата является преобразование Хейнса-Вулфа. Если в уравнении Михаэлиса-Ментен в обрат­ных координатах

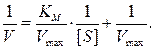
обе части умножить на величину [S], получим:

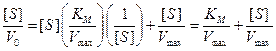
или

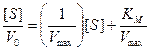
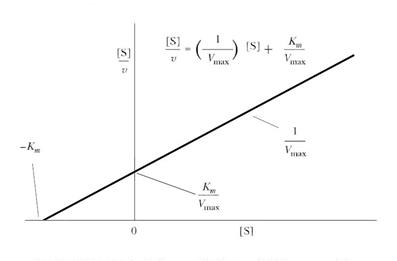
Рис. 6.3

График Хейнса-Вулфа в координатах [S]/V0 от [S], используемый для графического определения KM и Vmax.

График зависимости [S]/V₀) от [S] (рис. 6.3) представляет собой прямую линию, где тангенс угла наклона равен величине 1/V_max, длина отрезка, отсекаемого на оси у, будет равна K_M/V_max, а отрезок, отсекаемый на оси х, равен величине

–K_M.

Определение K_M имеет большую практическую ценность. При концентрациях субстрата, в 100 раз превышающих K_M, фермент будет работать практически с макси­мальной скоростью, поэтому максимальная скорость, V_max, будет отражать количество присутствующе­го активного фермента. Это немаловажное обстояте­льство используют для оценки содержания фермен­та в препарате. Знание величины K_M позволяет определить, какое количество субстрата следует внести в реакционную смесь для определения V_max. Графики, построенные в обратных координатах, находят широкое примене­ние также при анализе характера действия ингибиторов в ферментативных реакциях.