Проверка статистических гипотез о равенстве математических ожиданий и дисперсий

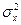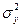Эффективность производственного процесса зависит от порождаемой им дисперсии, характеризующей разброс в данных. Таким образом, для определения эффективности нового режима работы, связанного с усовершенствованием обработки деталей, необходимо сравнить генеральные дисперсии и по данным выборок производительности труда.

При сравнении двух дисперси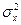й и 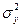выдвигают нулевую гипотезу Н₀: 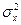= 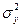; при конкурирующей Н₁: 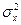≠ 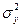. Если, по смыслу задачи, большей выборочной дисперсии ( ) заведомо не может соответствовать меньшая генеральная дисперсия, т.е. неравенство 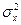< 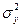заведомо невозможно, то конкурирующая гипотеза приобретает вид Н₁: 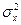> 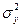. В этом случае для проверки альтернативной гипотезы Н₁ используется односторонний критерий Фишера

.

Здесь F_кр – критическое значение распределения Фишера (приложение Е), вычисленное при уровне значимости 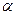и числах степеней свободы k₁ = n_x–1 и k₂ = n_y–1. Если указанное неравенство выполняется, мы склоняемся в пользу гипотезы
Н₁: 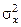> 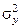, в противном случае, у нас нет основания отвергнуть нулевую гипотезу Н₀: = .

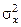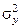В данном случае 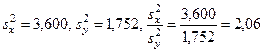. Из приложения Е при α = 0,05, k₁ = 9 и k₂ = 8 находим F_кр = 3,39. Так как 2,06 < 3,39, то мы не можем отвергнуть нулевую гипотезу и считаем равными генеральные дисперси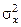и и 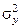. Это означает, что усовершенствование обработки деталей, в данном случае, не является эффективным.

При сравнении двух математических ожиданий a_x и a_у выдви­гают нулевую гипотезу Н₀ : a_x = a_у, при конкурирующей гипо­тезе Н₁ : a_x ≠ a_у. Методика проверки альтернативной гипотезы Н₁ зависит от соотношения генеральных дисперси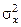й и .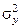

Ранее при сравнении двух дисперси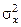й и 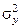нами было установлено, что 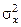= = 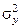. В этом случае оценкой дисперсии σ² является средневзвешенная выборочная дисперсия

.

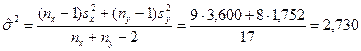Если заранее известно, что большему выборочному среднему ( 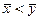), не может соответствовать меньшее математическое ожидание (a_у ≥ a_x), то альтернативная гипотеза принимает вид Н₁ : a_у > a_x. В этом случае для проверки альтернативной гипотезы Н₁ используется односторонний критерий Стьюдента

.

Здесь t_кр – критическое значение распределения Стьюдента (приложение Г), вычисленное при уровне значимости α и числе степеней свободы k = n_x+n_y–2. Если указанное неравенство
выполняется, то гипотеза Н₁ : a_у > a_x верна, в противном случае мы признаем справедливость нулевой гипотезы Н₀ : a_x = a_у.

В данном случае =42,33–40,60=1,73. Из приложения Г при α = 0,05 и k = 17 находим t_кр = 2,11, тогда

.

Так как 1,60 < 1,73, то мы склоняемся в пользу альтернативной гипотезы Н₁ : a_у > a_x. Следовательно, расхождение между выборочными средними и 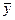неслучайно, при 5% уровне значимости оно является существенным и приводит к значимому повышению производительности труда после усовершенствования обработки деталей.

Отметим, что если при сравнении двух дисперси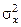й и 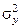было установлено, что 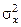> 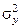( ), то для проверки гипотезы Н₁ : a_у > a_x следует использовать односторонний критерий Стьюдента вида

,

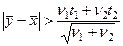где ; ; 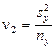t₁ и t₂ – квантили распределения Стьюдента (приложение Г), вычисленные при уровне значимости α и числах степеней свободы k₁ = n_x–1 и k₂ = n_y–1 соответственно.