Находим стандартную энергию Гиббса

.

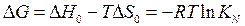∆G₀ = -20000 + 15,44 Т;

.

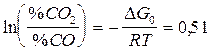%СО₂ / %СО = 1,73 или 36%СО и 64% СО₂ .

Однако, если реагирующие вещества находятся в растворе, то на равновесие обратимых реакций будут сильно влиять активные концентрации в растворе.

Термодинамика растворов

Растворами называются гомогенные многокомпонентные смеси переменного состава. В растворах частицы веществ равномерно распределены по объему и их концентрация может плавно изменяться в достаточно широких пределах. Последнее свойство отличает растворы от химических соединений, характеризуемых определенным количественным соотношением между входящими в их состав атомами.

Различают конденсированные ( твердые или жидкие ) и газовые ( газовые смеси ) растворы. Вещество, концентрация которого превышает 50%, являются растворителем, остальные компоненты – растворенными веществами.

Вещества имеют ограниченную растворимость, если после достижения определенной концентрации в равновесии с раствором находится свободное растворяемое вещество. Раствор, находящийся в термодинамическом равновесии – с нерастворенным остатком, называется насыщенным. Насыщение может также наступать в результате образования химических веществ между растворителем и растворяемыми веществами. Растворимость зависит от природы растворителя, содержания других компонентов, температуры и давления. Если исходные вещества раствора конденсированные, то влиянием давления пренебрегают.

Процесс растворения сопровождается двумя явлениями.

1. Рассеивание частиц по объему смеси – физическая сторона процесса.

2. Разрушение старых и образование новых связей между частицами однородных веществ в растворе – химическая сторона процесса.

Физическая сторона растворения изучает закономерность образования идеального раствора, когда характер связей между частицами в исходном и растворенном состояниях тождественен. Если связи различаются, то растворение сопровождается явлениями, характерными для химических реакций: тепловой эффект, изменение объема.

Современные теории растворов базируются на физической теории и учете химических явлений при растворении путем введения соответствующих поправок.

В сварочных процессах участвуют газовые смеси, металлические растворы и шлаки.

Газовые смеси в условиях сварочных температур являются идеальными растворами. Компоненты сохраняют свою химическую индивидуальность, а состав смеси поддается точному расчету методами химической термодинамики.

Металлические растворы разделяются на растворы внедрения и замещения.

Растворы внедрения образуются при растворении неметаллов О, Н, N, Р, С, S, В.

Растворы замещения образуются в сплавах и металлов, близких по параметрам кристаллической решетки и атомным радиусам.

Растворимость веществ при переходе из твердого состояния в жидкое резко возрастает. Однако жидкие и, тем более, твердые растворы существенно отличаются от идеальных. Различие ослабевает с ростом температуры.

Шлаки представляют собой сплавы окислов и солей металлов. Они образуются при сварке и пайке при плавлении флюсов и электродных покрытий.

В зависимости от характера изменения термодинамических свойств веществ при образовании раствора, различают следующие классы растворов:

1.Совершенный ( близкий к идеальному ) раствор. Энтальпия растворения Н_р = 0. Приращения энтропия ∆S_i = – R ln а_i , где а_i – активность i-ого компонента. Активность можно рассматривать, как исправленную мольную долю, при подстановке которой в уравнение идеальных растворов вместо N_i получается результаты, согласующиеся с опытом.

а_i = γ_i N_i

где γ_i – коэффициент активности, для совершенных растворов близок к 1, в особенности при высоких температурах.

Совершенными растворами являются растворенные в железе Со, Cr, Mn, Mo, W.

2.Неидеальный сильноразбавленный конденсированный раствор. В области малых концентраций γ_i ≠ 1, активность пропорциональна мольной доле. Коэффициент активности растворителя практически равен 1. Пример – растворы в железе меди и кремния.

3.Компонент с ограниченной растворимостью. При превышении концентрации выше критической в системе появляются чистый компонент, следовательно его активность

а_{i нас} = 1.

С другой стороны

а_{i нас} = γ_{i нас}N_{i нас}

Коэффициент активности γ_i = 1/ N_{i нас}

Для ненасыщенного раствора а_i = N_i / N_{i нас}

4.Регулярный раствор характеризуется тем, что приращение энтропии компонента i подчиняется закону идеальных растворов, но растворение сопровождается тепловым эффектом. Если допустить, что тепловой эффект слабо зависит от температуры, то

∆H_i = RT ln γ_i

Пример регулярных растворов – растворенные в железе Ni, Al, V.