Равновесное состояние термодинамической системы

На основе выше изложенного можно выделить основные особенности равновесного состояния изолированной системы:

самопроизвольность перехода системы в это состояние из любого предшествующего;

- единственность макросостояния при заданных термодинамических параметрах и бесконечное множество вариантов его реализации (микросостояний);

множество путей перехода в равновесие и случайный (принципиально непредсказуемый) выбор пути самой системой;

однородность в макромасштабах и максимальный беспорядок в микромасштабах (равновесный хаос);

наивысшая симметрия состояния;

необратимость перехода в равновесие и склеротичность системы: при переходе в равновесие стираются всякие следы предшествующего состояния, система «забывает», откуда пришла, прежнее состояние исчезает, и самопроизвольный обратный переход невозможен;

максимальность энтропии и равенство нулю ее изменения (производства):

d _i S _Р = 0, (5.6)

устойчивость к флуктуациям (флуктуация -случайное отклонение величин от некоторого среднего значения, т.е. случайное локальное упорядочение; флуктуации характерны для равновесного состояния, они постоянно возникают и исчезают, не нарушая его).

В целом равновесное состояние – предел эволюции изолированной системы, по достижении которого эволюция (какое-либо направленное изменение) прекращается.

Основы неравновесной термодинамики

Потоки и движущие силы

Все реальные системы являются закрытыми или открытыми и описываются на основе неравновесной термодинамики. В отличие от изолированных, такие системы обмениваются с окружающей средой: закрытые - энергией, открытые – помимо энергии веществом и информацией, те и другие – энтропией. Обмен характеризуется потоками, вызванными движущими силами. Рассмотрим два типичных неравновесных процесса: теплопроводность и диффузию.

Если по какой-либо причине в веществе (газе, жидкости, твердом теле) возникают неоднородность температуры или концентрации молекул (плотности), то тепловое движение молекул стремится выровнять эти неоднородности. При этом в среде возникают потоки энергии (тепла) или массы вещества. Эти явления получили название явлений переноса.

Пусть в среде вдоль координаты х уменьшается температура Т, т.е. имеется температурный градиент(характеризующий резкость изменения параметра в данном направлении), величина которого 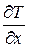. Он вызывает поток тепла I_Q, показывающий количество тепла, переносимого через единичную перпендикулярную градиенту поверхность за единицу времени. Фурье установил, что при сравнительно небольших градиентах поток переносимого тепла пропорционален градиенту температуры:

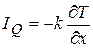. (5.7)

Аналогично при наличии градиента плотности вещества 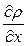в среде возникает диффузионный поток массы вещества I_m. Они связаны друг с другом законом Фика: поток переносимой массы вещества в диффузионных процессах пропорционален градиенту концентрации.

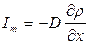. (5.8)

В уравнениях (4.7) и (4.8) k и D – соответственно коэффициенты теплопроводности и диффузии. В обоих случаях градиенты количественно определяют неравновесие в системе и являются движущими силами процессов.

Установленные в естествознании кинетические закономерности (5.7) и (4.8) исключительно важны для социально-экономических и других наук. Поэтому сделаем обобщения. Величины градиентов (температуры 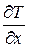и концентрации 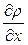) - движущие силы - называются обобщенной силой (X ), коэффициенты (k и D ) - коэффициентами эластичности системы. Если обобщенная сила не велика, то с точностью до знака обобщенный закон переноса (принцип линейности) формулируется следующим образом: поток прямо пропорционален обобщенной (движущей) силе.

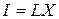(5.9)

Обобщенный закон или принцип линейности (5.9) успешно используется, например, при описании слабых неравновесных процессов в экономических системах, в которых возникают различные потоки: товаров, денег, ресурсов, рабочей силы, и т.д. Обобщенными силами, вызывающими эти потоки, могут быть различные цены – цена товара, цена рабочей силы, курс акций отрасли и т.п.