Определение массы тела по линейным измерениям.

Лабораторная работа № 2

Определение массы тела по линейным измерениям.

Точное взвешивание

При выполнении лабораторных работ преследуются следующие цели:

- углубление, конкретизация и систематизация знаний, полученных студентами на предыдущих этапах учебы;

- развитие умений и способностей самостоятельной учебно-познавательной и научно-исследовательской работы;

- формирование аналитического мышления, развитие рефлексии;

- контроль за степенью и характером усвоения учебного материала.

Оборудование: набор тел в виде цилиндров из различных материалов, линейка, штангенциркуль, весы лабораторные, разновес

Упражнение 1.

Определение массы тела по линейным измерениям.

1. Цель работы: закрепление теоретических знаний по теме 1.1 “Кинематика и динамика материальной точки”

приобретение практических навыков в работе с измерителями линейных размеров и с весами,

изучение методики расчетов средних величин.

2. Порядок подготовки к выполнению работы: изучить тему и материал лабораторной работы

3. Порядок выполнения лабораторной работы дан в упражнениях

4. Подведение итогов выполнения работы- предъявить результаты,

подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений

5. техника безопасности при выполнении лабораторной работы- стандартная

Цель работы: 1) научиться определять массу тела без его взвешивания; 2) изучить методики определения погрешностей прямых измерений; 3) изучить методику определения погрешностей косвенных измерений.

Объект измерений:геометрически правильная фигура, выполненная из известной марки стали, плотность которой приведена в справочнике по физическим свойствам веществ.

Основная формула:

M = ρ · V, где

ρ – плотность вещества, кг/м³,

V – объем, м³.

Измеряемые величины:

a, b, l – длина, ширина и высота фигуры;

d – диаметр (для осесимметричных фигур).

Измерительные приборы:линейка, штангенциркуль.

Метод Корнфельда для определения погрешности прямых измерений:

Если физическая величина измерена n раз, то надо: 1) выбрать из последовательности {х_n} x_max и x_min и определить среднее значение <x>= 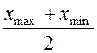; 2) найти абсолютную погрешность 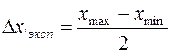; 3) определить погрешность ∆x_приб = (1/3)·h, где h – цена наименьшего деления шкалы измерительного прибора; 4) записать результат в виде 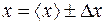с доверительной вероятностью α того, что истинное значение измеренной величины находится в интервале [<x>-∆x, <x>+∆x], которая вычисляется по формуле α=1-(1/2)^n-1. Результирующая погрешность ∆x= √(∆x_приб)²+(∆x_эксп)².

Метод расчета погрешностей Стьюдента:

Если физическая величина Х_i измерена n раз, то надо: 1) определить среднее значение <x>=∑Х_i/n; 2) определить среднеквадратичную погрешность среднего значения измеряемой величины Х по формуле

;

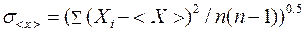3) выбрать доверительную вероятность α и по таблице коэффициентов Стьюдента определить по известному числу измерений и доверительной вероятности α коэффициент Стьюдента t_αn; 4) определить погрешность величины Х (доверительный интервал)

∆Х_эксп= t_αn· σ_<x>;

5) определить погрешность ∆x_приб=(1/3)·h, где h – цена наименьшего деления шкалы измерительного прибора; 6) определить результирующую погрешность ∆x= √(∆x_приб)²+(∆x_эксп)²; 7) записать результат 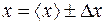с указанием доверительной вероятности α.

Метод расчета погрешностей косвенных измерений:

Если физическая величина Y есть функция непосредственно измеряемых величин {х₁, х_2,…х_n}, т.е. Y=f(х₁, х_2,…х_n), то ∆Y≈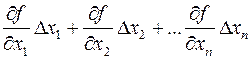

Задание №1.