От автоколебаний к самоорганизации

Для пояснения поведения открытых систем и их постижения удобным является использование аппарата нелинейных колебательных систем, разработанного в радиоэлектронике и связи, на фазовых портретах, изображенных на рис.9.

Первая автогенераторная система называется сис­темой с мягким возбуждением – любой электрический толчок (например, подключение источника питания) наводит в резонансной структуре некоторое и_m и сис­тема из первоначального состояния неустойчивого равновесия (и_m= 0) попадает в область Р₊ > Р_– (причем с плюсом – активность, с минусом – пассивность). При этом избыток энергии DР > 0 тратится на увеличение напряженности поля в резонаторе. Этот процесс продолжается до точки устойчивого динамического равновесия при и_m = и_s (движение показано стрелкой). Если какая-то внешняя сила выведет систему из этого состояния, например в область Р_->Р_+, то DР <0 и система должна уменьшить и_m, так как энергии источника недостаточно для поддержания колебаний с такой амплитудой.

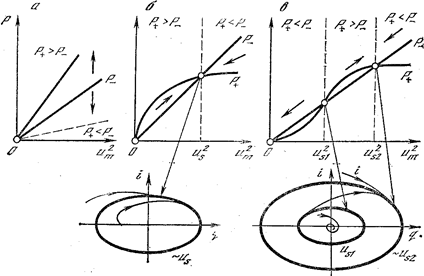
Рис.9. Виды режимов возбуждения колебательных и самоорганизующихся систем

Следовательно, система самостоятельно вернется в точку равновесия и_m = и_s (стрелка направлена справа налево). Во втором случае режим самовозбуждения называется жестким. В начальной области (малые и_m) Р_–> Р₊ и поведение системы аналогично только что рассмотренному случаю автогенератора с мягким возбуждением – система вернется в точку устойчивого равновесия при и_m = 0 (стрелка к началу координат). Таким образом, для выведения системы из состояния равновесия к ней необходимо приложить некоторый первоначальный толчок, обеспечивающий попадание ее в область и_m > и_s1. Поведение системы с жестким возбуждением при и_m > и_s1 в точности такое же, как и у автогенератора с мягким режимом самовозбуждения. Точка и_m = и_s1 является точкой неустойчивого равно­весия.

В нижней части рис.11 показано поведение мягкого и жесткого возбуждения автогенераторов на фазовой плоскости. Точкам равновесия на фазовой плоскости соответствуют предельные циклы колебаний (выделены жирными замкнутыми линиями). В теории колебаний доказаны теоремы существования и единственности предельных циклов.

Наличие на фазовой плоскости у некой исследуемой колебательной системы устойчивого предельного цикла свидетельствует о существовании в ней незатухающих колебаний.

Для всех типов генераторов общий принцип генерирования колебаний таков: генерирование колебаний есть процесс преобразования энергии некоторого источника (не обязательно электромагнитной природы) в энергию электромагнитных колебаний (или волн).

Таким образом, существуют два основных способа получения колебаний: за счет энергии источника постоянного тока (к примеру, электронные приборы) или за счет преобразования одних электромагнитных колебаний в другие с нужными параметрами (например, частотой). Наиболее характерными примерами последнего способа получения колебаний являются параметрические и квантовые генераторы.