Равновесие двухфазной системы

Рассмотрим переход системы между фазами 1 и 2, например, переход вода–пар в закрытом изолированном сосуде. Найдем химические потенциалы фаз в состоянии равновесия.

Для фазы 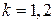из (2.57)

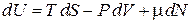
находим

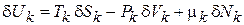. (2.57а)

Для изолированной системы

,

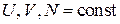тогда вариации

, , .

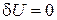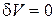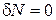Для отдельных фаз получаем

, , .

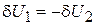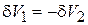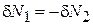Величины 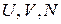являются аргументами энтропии 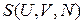. При переходе системы между фазами аргументы не меняются, тогда в равновесном состоянии энтропия системы минимальна и ее вариация

.

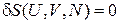Из (2.57а) выражаем вариации энтропии подсистем

.

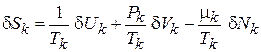Энтропия является аддитивной величиной, тогда для равновесной системы

.

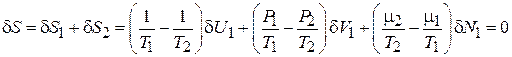Величины 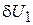, 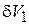и 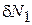взаимно независимые, это дает условия равновесия

,

,

.

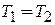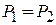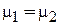При наличии внешнего поля

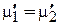. (2.60)

Электрохимический потенциал одинаков в разных фазах и в разных местах одной фазы равновесной системы.

Если химические потенциалы в разных фазах отличаются при одинаковых температурах и давлениях

, , ,

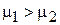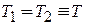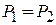то равновесия нет, и идет диффузия. Согласно второму началу термодинамики энтропия увеличивается

.

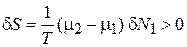Следовательно, dN₁ < 0 – частицы переходят из фазы 1 в фазу 2. Частицы перемещаются в ту сторону, где химический потенциал меньше, повышая его величину и выравнивая химические потенциалы.

Вычисление химического потенциала

Химический потенциал выразим через свободную энергию 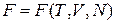и далее через статистический интеграл Z.

1. Выражаем химический потенциал через свободную энергию, используя формулы (2.31) и (2.57) для свободной и внутренней энергии

,

,

,

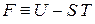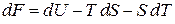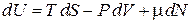получаем

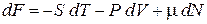. (2.61)

Из (2.61) находим

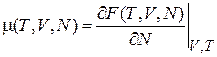. (2.61а)

Химический потенциал равен изменению свободной энергии при добавлении частицы, если система имеет постоянный объем и фиксированную температуру.

2. Выражаем химический потенциал через статистический интеграл, используя (2.19)

.

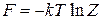Из (2.61а) получаем

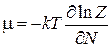. (2.61б)

Статистический интеграл идеального газа из 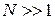частиц выражаем через статистический интеграл одной частицы

,

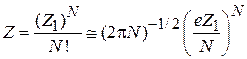где использована формула Стирлинга

.

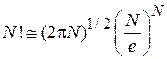Вычисляем

, ,

.

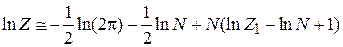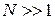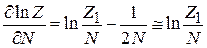Из (2.61б) находим химический потенциал многочастичного идеального газа

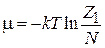. (2.62)

3. Для газа с поступательным движением частиц используем (2.22)

.

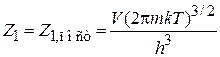Из (2.62) получаем

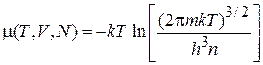, (2.62а)

где 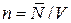– концентрация частиц. Химический потенциал увеличивается с ростом концентрации газа, с уменьшением температуры и массы частицы. При высокой температуре и низкой концентрации химический потенциал отрицательный, это соответствует условию применимости классической физики. При низкой температуре и высокой концентрации химический потенциал положительный и такая система описывается квантовой физикой.

Активность

Активность системы

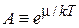
характеризует относительный вклад упорядочивающих и хаотических процессов системы в виде баланса между химическим потенциалом и тепловой энергией. При 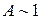система упорядочена, при 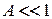система хаотична.

Используем (2.62)

,

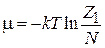находим

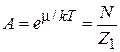. (2.62б)

Для газа с поступательным движением частиц

,

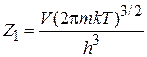получаем

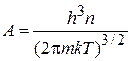. (2.62в)

При повышении температуры и уменьшении концентрации частиц активность упорядочивающих процессов понижается.

Для гелия при нормальных условиях

,

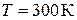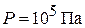
из (2.62а) и (2.62б) получаем

, .

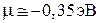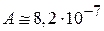Классический газ соответствует высоким температурам, низким концентрациям, большим расстояниям между частицами, когда преобладают силы притяжения, поэтому химический потенциал отрицательный и активность мала

, .
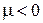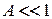