Свободного двухмерного газа?
Нерелятивистский двухмерный газ бозонов состоит из N частиц массой m, находящихся на площади S, и занимающих нижнюю зону размерного квантования. Используем
, 
,
.
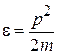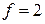Получаем не зависящую от энергии плотность состояний
,
и число частиц газа
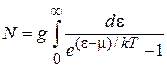. (П.13.5)
При изменении температуры число частиц сохраняется, тогда от температуры не зависит
.
Следовательно, при уменьшении температуры уменьшается модуль химического потенциала газа. Достижимо ли значение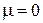 
при конечной температуре 
?
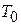В отличие от трехмерного случая, интеграл (П.13.5) при 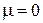и конечном T расходится на нижнем пределе. Действительно, на интервале энергии 
находим
,
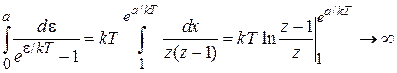где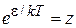 
, 
.
Получим зависимость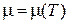 
. Вычисляем интеграл (П.13.5) и получаем
.
При 
разлагаем экспоненту в ряд 
при 
, и используем
.
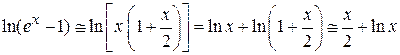Находим
,
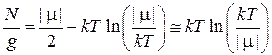. (П.13.6)
Следовательно, химический потенциал при любом числе частиц стремится к нулю только при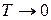 
. Бозе-конденсация свободного двухмерного газа при конечной температуре отсутствует.
ДВУХМЕРНЫЙ БОЗЕ-ГАЗ
В ПОТЕНЦИАЛЬНОЙ ЛОВУШКЕ
Двухмерный бозонный газ с числом частиц N удерживается ловушкой с потенциальной энергией
.
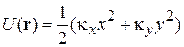Найдем температуру порога конденсации TC.
Для газа в параболической ловушке плотность состояний (П.8.2б)
,
где
, 
,
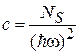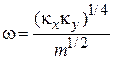тогда
.
При 
полагаем 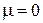и получаем число частиц
.
Используем
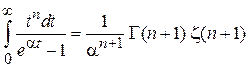
при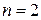 
, находим интеграл
.
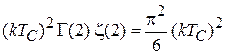Получаем
. (П.13.7)
В 2D-системе с пространственным ограничением бозе-конденсация происходит при конечной температуре.
РЕЙТИНГОВАЯ АТТЕСТАЦИЯ ПО ДИСЦИПЛИНЕ
Итоговое число баллов складывается из баллов, получаемых за каждый вид деятельности.
| № | Вид деятельности | Число баллов |
| 1. 2. 3. 4. | Активность на занятиях (выставляется в конце 6-ой, 12-ой и 18-ой недели) Индивидуальное задание 1 Индивидуальное задание 2 Индивидуальное задание 3 | (0–3) + (0–3) + (0–3)= 0–9 9–11 9–11 9–11 |
| 5. | Коллоквиум | Всего не более 40 |
| 6. | Экзамен: постановка задачи и качественный анализ результата + количественное обоснование результата + дополнительные вопросы по теме билета | Всего не более 60 0–20 0–10 0–10 |
Всего не более 100
МЕЖДУНАРОДНАЯ И РОССИЙСКАЯ ОЦЕНКИ
| Число баллов | Оценка | ||
| международная | российская | ||
| 90–100 | 97–100 93–96 90–92 | A+ A A– | отл. |
| 80–89 | 87–89 84–86 82–83 80–81 | B+ B B– C+ | хор. |
| 70–79 60–69 50–59 | 75–79 70–74 66–69 63–65 60–62 50–59 | C C– D+ D D– E | удовл. |
| 0–49 | 25–49 0–24 | FX F | неуд. |
Коллоквиум
1. Эрмитовые операторы, собственные функции и собственные значения. Условия ортонормированности для дискретного и непрерывного спектров. Операторы координаты и импульса. Соотношение неопределенностей.
2. Плотность вероятности. Плотность тока вероятности. Уравнение непрерывности. Пример: плоская волна.
3. Уравнение Шредингера для стационарного и нестационарного состояния. Пример – частица в потенциальной яме.
4. Спин электрона. Операторы, собственные функции, собственные значения. Принцип Паули и его обоснование.
5. Плотность квантовых состояний. Пример – трехмерный газ.
6. Распределение Ферми по состояниям и по энергии. Электронный газ в металле и в полупроводнике. Химический потенциал.
7. Распределение Бозе по состояниям. Химический потенциал. Фононный газ. Характеристики фонона. Распределение по частоте. Частота и температура Дебая.
Экзамен
1. Уравнение Шредингера для стационарного и нестационарного состояния. Краевые условия для прямоугольных потенциалов.
2. Плотность вероятности, ток вероятности, уравнение непрерывности. Изменение физической величины с течением времени. Пример.
3. Квазиклассическое квантование ВКБ. Туннельный эффект.
4. Модель Кронига–Пенни. Получение и анализ дисперсионного соотношения. Разрешенные и запрещенные зоны.
5. Модель Кронига–Пенни. Анализ дисперсионного соотношения. Зона Бриллюэна. Эффективная масса.
6. Локализация Андерсона. Уровни Тамма.
7. Уравнение Шредингера в сферической и цилиндрической системах координат. Плоский и пространственный ротаторы.
8. Атом водорода.
9. Заряд в однородном магнитном поле. Уровни Ландау.
10. Теория возмущений стационарных состояний невырожденного спектра.
11. Теория возмущений, зависящих от времени. Периодические возмущения.
12. Уравнение Паули. Эффект Зеемана.
13. Плотность квантовых состояний. Примеры.
14. Каноническое распределение квантовой системы. Вычисление колебательной и вращательной частей внутренней энергии.
15. Большое каноническое распределение фермионов и бозонов.
16. Электронный газ в металле и полупроводнике. Химический потенциал.
17. Двумерный и одномерный электронный газ.
18. Фотонный газ.
19. Фононный газ. Теплоемкость кристалла.
20. Конденсация Бозе–Эйнштейна.