Принцип неопределенностибыл сформулирован в 1927 г.В. Гейзенбергом: невозможно одновременно с абсолютной точностью указать положение микрочастицы и ее импульс.

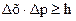(5.3)

или

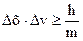, (5.4)

где Δх, Δр, Δv – точность определения координат, импульса и скорости частицы; h – постоянная Планка; m – масса частицы.

Принцип неопределенности означает, что нельзя одновременно точно определить положение и энергию электрона; можно говорить только о вероятности присутствия электрона в некотором объеме в данный момент.

В 1926 г. Э. Шредингер предложил для описания движения электрона в атоме волновое уравнение, получившее название уравнения Шредингера. Решением уравнения Шредингера является волновая функция ψ, называемая также орбиталью. Волновая функция может иметь как действительные, так и мнимые решения. Поэтому физический смысл имеет только квадрат модуля волновой функции |ψ|², который характеризует вероятность нахождения электрона в данном объеме пространства.Термином орбитальобозначают также область пространства, в которой наиболее вероятно нахождение электрона. Орбиталь может быть представлена, в частности, с помощью так называемых граничных поверхностей, т.е. пространственных фигур, внутри которых вероятность нахождения электрона составляет 95 %.

Решение уравнения Шредингера определяется набором четырех чисел, получивших название квантовых чисел.

Главное квантовое число n характеризует энергию орбитали. Главное квантовое число принимает значения 1, 2, 3, 4, 5, 6, 7…∞, обозначаемые также буквами K, L, M, N , O, P, Q … Чем больше n, тем выше энергия орбитали. Переходы электронов с одной орбитали на другую сопровождаются излучением или поглощением квантов энергии.

Главное квантовое число характеризует также удаленность максимума электронной плотности от ядра. Чем больше n, тем больше объем орбитали. Совокупность электронов с одинаковым значением n называют энергетическим уровнем или оболочкой, слоем, например К-уровень (К-оболочка, К-слой).

Орбитальное (побочное, азимутальное) квантовое число lпринимает значения от 0 до n-1 и характеризует форму граничной поверхности атомной орбитали. Обычно вместо численных значений используют буквенные обозначения: 0-s; 1-p; 2-d; 3-f и т.д. Совокупность электронов, имеющих одинаковые значения l и n, называют энергетическим подуровнем(подоболочкой), например 1s-подуровень (n=1; l=0); 2p-подуровень (n=2; l=1) и т.д.

Граничная поверхность s-орбиталей имеет форму сферы (рис. 5.1,а), р-орбиталей – гантели (рис. 5.1,b–d). Граничные поверхности d-орбиталей показаны на рис. 5.1,e–i. Форма граничных поверхностей f-орбиталей сложнее, чем d-орбиталей.

Орбитальное квантовое число характеризует также энергию электронов подуровня в пределах данного энергетического уровня.

Энергия подуровней возрастает в ряду s, p, d, f (E_s<E_p<E_d<E_f).

Магнитное квантовое число m_l характеризует ориентацию орбитали в пространстве и может принимать целочисленные значения от +l до –l, включая 0. Например, для d-подуровня (l=2) магнитное квантовое числа может иметь значения -2, -1, 0, 1, 2. Таким образом, d-орбиталь может иметь пять ориентаций в пространстве (рис. 5.1,e–i). Одновременно это означает, что d-подуровень содержит пять орбиталей, s-подуровень – одну (рис. 5.1,a), p-подуровень – три (рис. 5.1,b–d), а f-подуровень – семь орбиталей.

Атомной орбиталью называют также волновую функцию, характеризуемую определенным набором трех квантовых чисел ( ).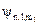

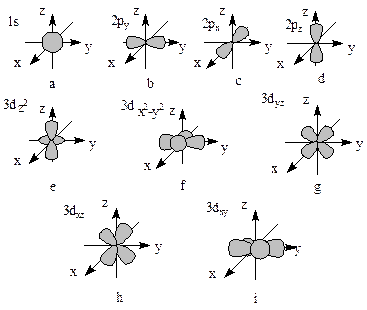
Рис. 5.1. Формы граничных поверхностей атомных орбиталей: a–1s; b–2p_y; c–2p_x; d–2p_z; e–3d_z2; f–3d_x2_-y2; g–3d_xy; h–3d_xz; i–3d_xy.

Спиновое квантовое число m_sхарактеризует собственное вращение электрона вокруг своей оси и может принимать два значения: +1/2 и -1/2.

Таким образом, состояние электрона в атоме полностью характеризуется с помощью четырех квантовых чисел: n, l, m_l и m_s.

Строение многоэлектронных атомов.Следующие принципы (правила) определяют заполнение электронами энергетических уровней и подуровней:

1) принцип исключения Паули (запрет Паули);

2) принцип наименьшей энергии;

3) правило Клечковского;

4) правило Гунда.