Закон изомеризации. Общая теория изомерии. Изомерия и симметрия

Остановимся далее на третьем способе порождения объектов-систем — изменениях одних отношений между «первичными» элементами на другие. Одновременно приведем решающие до­казательства эвристичности нашего варианта ОТС.

Предложение 10. Третий закон преобразования композиций системы. Если в системе S_i, в которой объекты-системы, изменяя одни отношения между «первичными» элементами на другие, переходят в иные два и более объектов-систем, то в ней имеет место изомерия.

Доказательство. Изомерия есть система объектов одного и того же рода, состоящая из объектов-систем, одинаковых по составу — числу и виду —«первичных» элементов, но различных но взаимоотношениям последних. Математически изомер суть перестановка, изомерия — множество перестановок, или разме­щений, из n «первичных» элементов по n. Из сказанного видно, что условие предложения 10 и условия, приводящие к существо­ванию изомерии, а именно тождественность по составу и разли­чия по межэлементным отношениям, совпадают. Отсюда в систе­ме S с f такими подмножествами М_i^(S) (f=1, 2, 3, ...; i = 1, 2, 3, ..., f), композиции которых одинаковы по соответствующему для i-го подмножества составу «первичных» элементов, но раз­личны по взаимоотношениям последних, по определению должно иметь место f различных изомерий. Предложение 10 доказано.

Действию закона изомеризации подвержены все формы дви­жения материи. Поэтому изомерия должна быть присуща каж­дой из них, что и подтверждается открытиями изомерии — химической (Ф. Велером, Ю. Либихом, И. Я. Берцелиусом в 1822—1830 гг.), ядерно-физической (О. Ганом в 1921 г.), биологической (Ю. А. Урманцевым в 1956—1957 гг.), социаль­ной (Ю. А. Урманцевым в 1974 г.), геологической (И. П. Ша­раповым, В. Ю. Забродиным в 1977—1979 гг.). Открытие геологической изомерии и детальное ее изучение были осуществле­ны на основе предсказаний нашего варианта ОТС и благодаря детальному использованию общей теории изомерии, развитой в его рамках. В монографии «Симметрия природы и природа симметрии» [91] мы привели примеры химической, ядерно-физической, биологической и социальной изомерии, а в монографии В. Ю. Забродина «Системный анализ дизъюнктивов» [29] да­ны многочисленные примеры геологической изомерии.

Закону изомеризации подчиняются не только формы движения, но и формы существования материи. Учет этого обстоятельства способствовал резкому расширению традиционного учения об изомерии благодаря выводу о существовании не только изомеров-структур (тел), но и изомеров-пространств, изомеров-движений, изомеров-времен [88; 91; 92]. В табл. 5 приводится перечень 4 основных и 64 основных и производных изомерий важнейших форм существования материи, причем в этом списке 63 изомерии оказались новыми, а 15 связаны только с пространством, временем, движением.

В упомянутой книге мы привели примеры изомеров-пространств, изомеров-движений, изомеров-времен. Здесь дадим примеры только изомеров-пространств. Очевидно, в соответст­вии с законом изомеризации изомерией пространств мы должны считать явление существования множества пространств одного состава, но с различными межэлементными отношениями. Таковы, например, пары левых и правых диссимметрических пространств — континуумов, семиконтинуумов, дисконтинуумов, классическая симметрия которых исчерпывается лишь элемента­ми первого рода. Понятно, что с точки зрения теории диссфакто-ров [94] или, скажем, кратной антисимметрии [30] каждое такое изомерное множество может состоять не только из пары, но и из большего числа изомерных пространств. Другим приме­ром является множество состояний пространства, которые пе­реходят друг в друга в результате различных автоморфизмов — одно-однозначных отображений данного пространства на себя.

Таблица 5. Список 64 фундаментальных изомерии и симметрии (из них новых изомерии — 63, новых симметрий — 60,61;

П — пространственная, В — временная, Д — динамическая, С — субстанциональная)

№ п. п.	Изомерия (симметрия)	№ п. п.	Изомерия (симметрия)	№ п. п.	Изомерия (симметрия)
	П		двп		ВПДС
	В		пдс		В ДПС
	Д		псд		ДПВС
	с		дпс		двпс
	пв		ДСП		пдсв
	вп		спд		псдв
	пд		сдп		дпсв
	дп		вдс		дспв
	ПС		вед		спдв
	СП		две		сдпв
	вд		дев		вдсп
	дв		сдв		всдп
	ВС		спд		двсп
	ев		иве		дсвп
	дс		пев		свдп
	сд		впс		сдвп
	пвд		всп		пвсд
	пдв		спв		псвд
	впд		свп		впсд
	вдп		пвдс		вспд
	дпв		пдвс		спвд
					свпд

Таблица 6. Список 54 структурных изомерии и симметрии
(из них новых изомерий — 53, новых симметрий — 40; под. - подобия, конф.— конформная, афф.— аффинная, пр.- проективная, топ— топологическая, кр.— кратная, цв. - цветная)

№ п.п. Изомерия (симметрия)	№ п. п. Изомерия (симметрия)	№ п.п Изомерия (симметрия)
1 классическая	19 конформная	37 проективная
2. анти-	20 конф. анти-	38 пр. анти-
3 кр. анти-	21 конф. кр. анти-	39 пр. кр. анти-
4 цв.	22 конф. цв.	40 пр. цв.
5. цв. анти-	23 конф. цв. анти-	41 пр. цв. анти-
6. цв. кр. анти-	24 конф. цв. кр. анти-	42 пр. цв. кр. анти-
7. кр. цв.	25 конф. кр. цв.	43 пр. кр. цв.
8. кр. цв. кр. анти-	26 конф. кр. цв. кр. анти-	44 пр. кр. цв. кр. анти-
9. крипто-	27 конф. крипто-	45 пр. крипто-
10. подобия	28 аффинная	46 топологическая
11. под. анти-	29 афф. анти-	47 топ. анти-
12. под. кр. анти-	30 афф. кр. анти-	48 топ. кр. анти-
13. под. цв.	31 афф. цв.	49 топ. цв.
14. под. цв. анти-	32 афф. цв. анти-	50 топ. цв. анти-
15. под. цв. кр. анти-	33 афф. цв. кр. анти-	51 топ. цв. кр. анти-
16. под. кр. цв.	34 афф. кр. цв.	52 топ. кр. цв.
17. под. кр. цв. кр. анти-	35 афф. кр. цв. кр. анти-	53 топ. кр. цв. кр. анти-
18. под. крипто-	36 афф. крипто-	54 топ. крипто-

Классификация изомерии по виду операций, посредством которых одна изомерная структура переходит в другую изомер­ную структуру, позволила вывести 54 структурные изомерии, из которых 53 оказались существенно новыми. Это крипто-, про­стые и кратные анти- и (или) цветные — классическая, подобия, конформная, аффинная, проективная, топологическая изомерии (см. табл. 6).

В настоящее время закончено построение моделей каждой из 54 изомерий, кроме того, установлена возможность удвоения, утроения и т. д. числа структурных изомерий за счет изменения закона комбинирования качеств ( + , —; цветных, крипто-) как друг с другом, так и с основными геометрическими преобразова­ниями (евклидовыми, подобия, конформными и т.д.).

Изучение с точки зрения ОТС даже известной стереохимикам оптической, или, строже, диссимметрической изомерии, по­могло нам [94] доказать существование трех типов диссизомерий: I типа (старого), число изомеров S для которого S_k° ^k° = 2 ^k° (изомерия альдогексоз и листьев липы); II типа (нового), S для которого

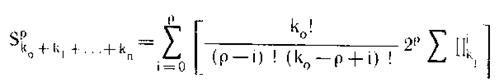
(его примеры — изомерия пираногексоз и изолированных корней некоторых растений); III типа (также нового), S для которого S¹_o+k1 =2k₁ (изомерия пираногексоз с k₀ = 0 и циклических вен­чиков с нечетным числом взаимно перекрывающихся лепестков).

Проанализируем теперь связь учения об изомерии с теорией групп и симметрии, центральным предложением ОТС и пробле­мой «состав — строение — свойство». Тем самым мы продолжим построение общей теории изомерии.

Изомерия и симметрия. Связь изомерии с симметрией дока­зывается посредством теории групп подстановок. Дело в том, что эту теорию и вообще математическое учение о перестановках содержательно можно интерпретировать как учение об изоме­рии. В самом деле, с точки зрения математики изомер — это перестановка, изомерия — множество перестановок, изомериза­ция — это подстановка, верхняя строка которой означает пред­мет, а нижняя — результат изомеризации; следующие друг за другом изомеризации есть произведение подстановок. Совокуп­ность всех подстановок для действия умножения подстановок образует группу подстановок. Следовательно, совокупность всех изомеризации для действия «умножения» изомеризации также образует группу — группу изомерии, а следовательно, выявляет и определенного рода изомерийную симметрию, которая пред­стает как сохранение состава изомеров при изомеризациях. Благодаря этим операциям одни изомеры данной совокупности переходят в другие изомеры той же совокупности, а вся совокуп­ность по составу «первичных» элементов и составу изомеров «совмещается сама с собой». Сказанное позволяет сформулиро­вать следующее предложение.

Предложение 11. Всякая конечная группа всех изомеризации n-й степени — группа I_n — изоморфна группе всех подстановок n-й степени — группе S_n.

Математический изоморфизм теории групп подстановок тео­рии групп изомерии позволяет автоматически переносить зна­ния из первой области во вторую. В частности, имеет место следующее.

Теорема Кэли. Всякая конечная группа порядка n изоморф­на некоторой подгруппе группы всех подстановок n-й степени. Следующее предложение — ее изомерийный аналог.

Предложение 12. Всякая конечная группа порядка n изомор­фна некоторой подгруппе группы всех изомеризации n-й степени. Отсюда сразу получаем предложение 13.

Предложение 13. Всякая конечная группа симметрии поряд­ка n изоморфна некоторой подгруппе группы всех изомеризации n-й степени.

Изоморфизм симметрии и изомерии, установленный здесь по крайней мере для их конечных групп, позволяет — благодаря возможности переноса знаний из одной области в другую — по меньшей мере, во-первых, считать список 64 фундаментальных и 54 структурных изомерии списком также 64 фундаментальных и 54 структурных симметрий. Сказанное объясняет, почему упомянутые таблицы 5 и 6 есть таблицы также симметрии — известных и впервые найденных; во-вторых, ввести представле­ния о непрерывных и дискретных преобразованиях изомерии, конечных и бесконечных группах изомерии; в-третьих, ввести представление о размерности изомерии.

Будем считать изомерию n-мерной (n = 0, 1, 2, 3), если каждый изомер данной совокупности обладает n-мерной симмет­рией — точечной, линейной, плоской, пространственной. Напри­мер, изомерия асимметричных альдогексоз состава С₆Н₁₂О₆ или асимметричных листьев липы — 0-мерная, потому что каждому из 16 изомеров соответственно альдогексозы и листа липы при­суща точечная группа симметрии (1). Изомерия побегов расте­ний с левым или правым листорасположением — одномерная, потому что каждому изомеру побега присуща одномерная, или линейная, симметрия, описываемая одной из групп симметрии «стержней». Однако нередко при изомеризациях симметрия изо­мера меняется. Например, в зависимости от ионной силы и тем­пературы раствора молекулы РНК могут существовать то в виде «клубков», обладающих точечной симметрией, то в виде «нитей», обладающих одномерной симметрией. Соответственно и изоме­рия таких объектов будет не n-мерная, a n₁ — n₂ —...— n_k -мерная. В приведенном примере она 0—1-мерная.

В-четвертых, появляется возможность предложить новую идею о возможности развития теории групп n₁ — n₂ —...— n_k -мерной симметрии, в которой размерность объекта при преобра­зованиях симметрии уже не оставалась бы инвариантной.

В-пятых, это позволяет сделать новый для классической теории структурной симметрии вывод о возможности реализации любого диссимметрического (правого или левого) или недиссимметрического объекта соответственно в виде не двух или одного, а двух или большего (в пределе бесконечного) числа модифика­ций. Данный вывод прямо следует, например, из возможности существования любого диссимметрического или недиссимметри-ческого изомера в виде двух или большего числа изомерных, а шире — полиморфических модификаций. Тот же вывод следует из развитой нами теории диссфакторов [91; 94].

Изомерия и центральное предложение ОТС. Казалось бы, изомерия может быть порождена только благодаря относитель­ному преобразованию. Однако в статье «О значении основных законов преобразования объектов-систем для биологии» мы писали «о возможности возникновения изомерии от исходных объектов всеми семью способами» [98. С. 132]. В табл. 7 приве­дены «лингвистические», разумеется сугубо условные, модели всех семи способов порождения изомерии. Из таблицы видно, что вопреки широко распространенным представлениям изоме­рия может возникнуть посредством, казалось бы, и неизомеризационных способов.

Таблица 7. Лингвистические модели порождения изомерии — множества {сон, нос} — семью способами

№	Способ	Модель
	Количественный	сонный ------ (- «ный»)-------à сон ноский -------( - «кий») ------à нос
	Качественный	кон --------- ( к->с ) --------à сон нож ---------- ( ж ->с) --------à нос
	Относительный	нсо --------------------------------------à нос нсо ---------------------------------------à сон
	Колич + Кач	соринка --- (-«инка») àсор --- р->н --à сон тоска --------(-«ка») ---à тос ---т->н --à нос
	Колич + Относ	носки ---- (- «ки») ---à нос -----------à сон сновидение –(- «видение») --à сно --à нос
	Кач + Относ	дом --- (д ->с)—(м ->с) ---àнос -------à сон сор --------( р ->н ) ---------àсон -------à нос
	Колич + Кач + Относ	домкрат –(-«крат») àдом –(д-> н)—(м-> с) àнос à сон соратник --(-«атник»)--à сор--- –(р ->н )-- àсон --à нос

Столь же неверным является и другое традиционное мнение, будто сугубо изомеризационное — относительное — преобразо­вание всегда приводит к возникновению изомерии. В действи­тельности такое преобразование может приводить к превраще­нию изомерной совокупности в изомерную же (например, мно­жества {сон, нос} — во множество {нсо, сно}), неизомерной — в неизомерную (например, множества {сон} — во множество {нос}), неизомерной — в изомерную и наоборот (например, мно­жества {сон} — во множество {нос, нсо} или множества {нос, нсо} — во множество {сон}).

Неправильным оказывается и третье традиционное представ­ление о том, что лишь при относительном преобразовании состав изменяемых объектов не изменяется. В действительности и шесть остальных —«неизомеризационных»— преобразований могут породить изомерию без изменения состава исходных объектов (см. табл. 8). Если бы «реакции» (табл. 8) протекали в обратном направлении, то мы получили бы лингвистические модели порождения неизомерной совокупности (сон) из изомер­ной {нос, онс} без изменения состава посредством шести «неи­зомеризационных» способов.

Табл. 7, 8 позволяют также сделать вывод о том, что при изучении процессов во времени важно учитывать порядок пре­образований. Это приводит к необходимости оперирования уже не с сочетаниями, а с размещениями четырех основных преобра­зований, т. е. не с åC₄ⁱ= 15, а, в частности, с åA₄ⁱ = 64 преобра­зованиями. Только такой подход дает возможность правильно представить реальные механизмы преобразования совокупно­стей объектов-систем.

Далее. Эти же таблицы помогают избежать скоропалитель­ных выводов о характере механизма тех или иных процессов исходя из знания лишь исходных и конечных продуктов «ре­акции», поскольку им могут быть присущи самые различные механизмы.

В табл. 7 приведены лингвистические модели семи способов порождения изомерии. Очевидно, таких вариантов порождения изомерии было бы лишь семь, если бы изомерия могла возни­кнуть под действием только любого одного из семи способов преобразования на каждый объект исходной совокупности. Од­нако объекты исходной совокупности — {Ми}— могут быть пре­образованы в объекты-изомеры изомерной совокупности — {Миз} —«действием» не только одного из семи, но и любых двух, трех из восьми, наконец, восьми из восьми способов преобразования. И тогда число возможных вариантов преобразования {Ми} в {Mиз} равнялось бы C^l₇ + C²₈ + C³₈+.. .+ С⁸₈ = 254.

Таблица 8. Лингвистические модели порождения изомерии — множества (нос, онс) шестью «неизомеризационными» способами без изменения состава исходного объекта

№	Способ	Модель
	Количественный	сон ------ (- «с», -«н»)---- à о ---(+ «н», +«с»)à нос сон ------ (- «с», -«н»)---- à о ---(+ «н», +«с»)à онс
	Качественный	сон ------(с-> н) --------- (н ->с )------------------ à нос сон ------(с-> о) --------- (о ->н ) ---- (н->с )-----à онс
	Колич + Кач	сон -- (-«с») àон - (+«с») à онс-(н-> о)-- (о ->н ) à нос сон -- (-«н») àсо - (+«н») à нсо-(н->о)- (с->н)- (о ->с ) à онс
	Колич + Относ	сон -- (-«с») àон ---- (+«с»)----à онс----------à нос сон -- (-«н») àсо -----(+«н»)--- à нсо----------à онс
	Кач + Относ	сон ------(н-> о) --------- (о ->н )---- à сно ----------- à нос сон ------(с-> н) --------- (н ->с ) ----à нос -----------à онс
	Колич + Кач + Относ	сон -- (-«н») àсо - (+«н»)à нсо-(н->о)- (с->н)- (о ->с ) à онс àнос сон -- (-«с»)àон - (+«с») à онс-(о->н)- (н->с) àнос à онс

Здесь первый член суммы взят в виде С¹₇, а не С¹₈, потому что учтено следующее обстоятельство: само по себе тождественное преобразование не может породить изомерию, переводя {M_и} сно­ва в {M_и}. Однако в сочетании с другими способами оно может приводить к изомерии. Например, пусть {M_и} = {сон}, т. е. состоит из одних лишь слов «сон». Если бы на эту совокупность «дей­ствовал» лишь один из способов, например 3 —«относительный», и только так, что каждое слово «сон» из {M_и} он превращал бы только в слово «нос», то мы получили бы новое множество М = {нос) и изомерия не возникла бы. Однако та же самая совокуп­ность {M_и} = {сон) могла бы быть преобразована в {M_из} = {сон, нос} в результате «частичной изомеризации», т. е. если бы на одну ее часть «действовало» тождественное, на другую — относительное преобразование. Естественно, тождественное преобразование может комбинироваться и с любыми другими преобразованиями из семи возможных для объектов-систем, и точно так же (хотя бы в согласии с табл. 8) приводить к изомерии.

Разумеется, если бы «реакции» протекали в обратном направлении, то число возможных преобразований {M_из} в {M_и} то­же равнялось бы 254. В результате доказано следующее предло­жение.

Предложение 14. Неизомерная совокупность объектов-сис­тем может быть преобразована в изомерную и наоборот 254 раз­личными способами.

По-видимому, данные преобразования можно рассматривать как модель преобразований любых совокупностей объектов-систем, в том числе изомерийно-неизомерийных. Если к тому же в целях логической полноты учитывать как отдельное преобразо­вание и тождественный переход, то способов преобразований одних совокупностей в другие будет, естественно, не 254, а 255. Тот же результат имеем по формуле

_{n 8}

å Cⁱ_n = 2ⁿ-1 т. е. å Cⁱ₈ = 2⁸-1 = 255, что и требуется предложением 4.

^{i=l i=l}

Разумеется, при различении порядка преобразований (а это важно, например, при изучении протекания реакций во времени) число вариантов «переделок» может возрасти до бесконечности из-за многократных реализаций одних и тех же преобразований. Очевидно, лишь при однократном их «использовании» число таких вариантов было бы равно

₈

å Aⁱ₈ = 109 600

^i=l

Аналогично, если бы мы исходили не из центрального предложения ОТС, а из более дробной табл. 1, т.е. не из 8, а из 15 основных и про­изводных преобразований объекта-системы, то мы также имели бы не 255, а

₁₅

å Сⁱ₁₅ = 32 767

^i=l

вариантов преобразований одних совокупностей объектов-систем в другие.

Изомерия и проблема «состав — структура — свойство». Во­прос о строении и свойствах изомеров — один из самых фунда­ментальных и практически значимых. Тем не менее до сих пор нет строгих ответов на следующие вопросы: 1. Обязательно ли различия изомеров по строениям (межэлементным отношениям) влекут за собой различия их и по свойствам? 2. Неизбежно ли различия изомеров по свойствам обусловливают их различия и по строению? 3. Насколько изомеры могут отличаться друг от друга? Если учесть, что об отличиях объектов друг от друга обычно судят по различиям их отношений к другим объектам, то ответом па вопросы 1 и 3 является предложение 15.

Предложение 15. Если два изомера (И₁, и И₂) различаются но строению, то они отличаются друг от друга и по бесчисленно­му множеству отношений R_j (j = l, 2, ..., ¥) к другим объек­там. Истинность предложения 15 следует из истинности значи­тельно более общего утверждения.

Предложение 16. Если два произвольных объекта А и В раз­личаются хотя бы по одному признаку П так, что П_А ¹ П_В, то тогда существует бесчисленное множество отношений R_j (j = l, 2, 3, ..., ¥) к другим объектам, по которым они также различа­ются. Это суждение нами высказывалось и раньше, например в статье «Начала общей теории систем» [см. 92], но там оно не было доказано. Поэтому обоснуем его справедливость.

Первоначально примем во внимание следующую аксиому: «Пусть А и В — различные объекты. Тогда существует хотя бы одно отношение R с другими объектами, по которому А и В не тождественны. В противном случае А и В тождественны».

Из аксиомы следует, что если произвольные А и В — различ­ные объекты, то для них существует хотя бы одно отношение — обозначим его R₁,— по которому они не тождественны, т.е. R₁A ¹ R₁B. Однако, согласно этой же аксиоме, для R₁A и R₁В су­ществует по крайней мере одно отношение — обозначим его R₂,—по которому они также нетождественны, т.е. R₂R₁A ¹ R₂R₁B; далее для R₂R₁A и R₂R₁B существует хотя бы одно отношение R₃, так что R₃R₂R₁A ¹ R₃R₂R₁B. И вообще для любых R_nR_n-1 ... R₁A и R_nR_n-1, . . . R₁B существует хотя бы одно такое отношение R_n+l, при котором R_{n + 1}R_n ... R₁A ¹ R_n+1R_n ... R₁B и так до бесконечности. Следовательно, предложения 15, 16 ис­тинны.

Кстати, хорошей фактической иллюстрацией к сказанному служат так называемые зеркальные — правые (D) и левые (L) — химические изомеры, например D- и L-глицериновые аль­дегиды. Такие изомеры действительно отличаются друг от друга по бесчисленным отношениям к другим объектам — к линейно, кругово, эллиптически- поляризованному свету, к множест­ву D и L элементарных частиц, к бесчисленному множеству D и L химических соединений, к D и L биообъектам, людям правшам и левшам и т. д.

Ответ на вопрос «Обязательно ли различие изомеров по свойствам указывает на их различия по строению (межэлемент­ным отношениям)?» дает предложение 17.

Предложение 17. Если два изомера (И₁ и И₂) различаются по свойствам, то они отличаются друг от друга и по строению. Как и ранее, о различиях изомеров по свойствам будем судить по различиям их отношений к другим объектам. Тогда спра­ведливость предложения 17 можно установить посредством сле­дующего суждения.

Предложение 18. Если два произвольных объекта (А и В) различаются хотя бы по одному отношению R так, что RA ¹ RB, то они обладают таким, хотя бы одним, признаком П, что ПА ¹ ПВ.

Предположим, что А и В не обладают хотя бы одним призна­ком П, по которому они различаются. Тогда эти объекты тожде­ственны и, согласно приведенной аксиоме, не должно быть отношения R, по которому они различались бы. Однако такое отношение существует, и, следовательно, объекты А и В различ­ны, поэтому существует хотя бы один признак П у А и В, по которому они различаются.

В случае изомеров как изомеров-систем таким П не может быть состав и закон композиции: по этим признакам они, по определению изомерии, тождественны. Остается лишь один при­знак — различия по межэлементным отношениям (строению). Следовательно, из различия изомеров по их свойствам действи­тельно следует сделать вывод об их отличии друг от друга по строению, т. е. по межэлементным отношениям.

Таким образом, с точки зрения закона изомеризации изоме­рия не всеобща, она присуща лишь определенному классу сис­тем. В то же время требованиям данного закона отвечают специ­альные случаи каждой формы движения и каждой формы су­ществования материи. Уже одно это позволяет считать изомерию общенаучной категорией. Однако изомерия имеет не только общенаучный, но и глубокий философский смысл, и пре­жде всего потому, что относительный способ превращения объектов-систем (переход одних отношений между «первичны­ми» элементами в другие) суть не просто рядовой способ превра­щения, а форма изменения материи, далее неразложимая и не­сводимая к другим ее формам. Как уже говорилось, с точки зрения ОТС относительная форма изменения материи — это один из четырех основных, «первичных» способов преобразова­ния одних объектов-систем в другие.

К сожалению, фундаментальный характер изомерии, имею­щей непосредственное отношение к генезису, симметрии, соста­ву — структуре — свойствам объектов неживой, живой природы и общества, ни философами, ни специалистами других областей знания в должной степени до сих пор не осознается.