При высокой температуре возбуждены все моды колебаний и для малопрочных кристаллов выполняются законы классической физики.

При низкой температуре часть мод не возбуждается, «вымерзает», и для прочных кристаллов существенны квантовые свойства.

Теплоемкость при высоких температурах. Для малопрочных кристаллов выполняется 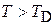. Верхний предел интеграла (4.71)

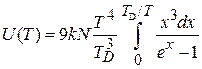
меньше единиц, тогда . Экспоненту разлагаем в ряд, ограничиваемся двумя слагаемыми , и получаем

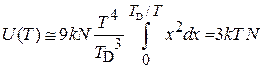. (4.73)

Теплоемкость

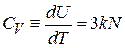
удовлетворяет закону Дюлонга–Пти классической физики.

Теплоемкость при низких температурах. Для прочных кристаллов выполняется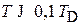. Верхний предел интеграла (4.71)

,

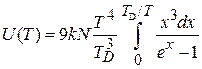с учетом подынтегральной экспоненциальной функции, считаем бесконечным. Используем

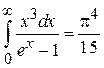
и получаем внутреннюю тепловую энергию кристалла

, (4.74)

где учтено (4.69)

.

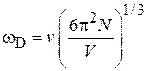Результат аналогичен внутренней энергии фотонного газа (4.63)

, .

Для теплоемкости кристаллической решетки прочных кристаллов получаем закон Дебая

. (4.75)

При низких температурах теплоемкость кристалла пропорциональна третьей степени температуры.

Теплоемкость для широкого интервала температур. Используем (4.71)

,

,

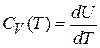и получаем

. (4.76)

ПРИМЕРЫ

1.Получить вероятность обнаружения фонона 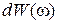с частотой в интервале 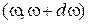в единице объема кристалла при низких температурах. Найти концентрацию фононов, наиболее вероятную энергию и длину волны.

Искомая вероятность

, ,

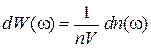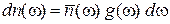где n – концентрация фононов. Используем (4.70)

, .

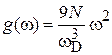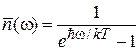Находим

, (П.12.1)

где N – числом элементарных ячеек в кристалле объемом V.

Нормировка вероятности

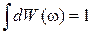
дает концентрацию фононов

.

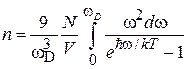Заменяем 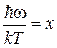, используем , и получаем

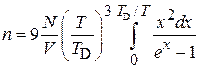. (П.12.2)

Низкая температура 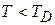. Верхний предел интеграла считаем бесконечным

,

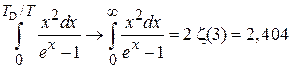тогда

. (П.12.3)

При низких температурах в трехмерном кристалле средняя концентрация фононов пропорциональна числу элементарных ячеек в единице объема кристалла и третьей степени температуры. При 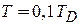получаем – концентрация фононов составляет сотые доли от концентрации элементарных ячеек кристалла.

Вероятность обнаружения фонона в единице объема в единичном интервале частоты около значения w находим из (П.12.1)

и (П.12.3)

,

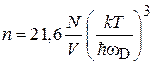в результате

. (П.12.4)

При низкой частоте 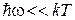из (П.12.4) получаем

.

При высокой частоте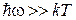

.

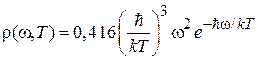Максимум функции

,

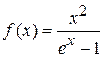где 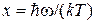, соответствует наиболее вероятной частоте w_m фонона. Из условия

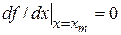
получаем уравнение

.

Численное решение дает

.

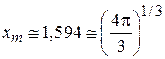Наиболее вероятная энергия фонона

.

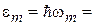
Учитывая (4.72)

,

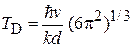находим наиболее вероятную длину волны

,

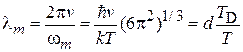где d – постоянная решетки. При низкой температуре наиболее вероятная длина волны фонона во столько раз превышает постоянную решетки, во сколько раз температура кристалла меньше температуры Дебая.

2.Найти давление фононного газа при .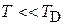

При низкой температуре внутренняя энергия фононного газа (4.74)

. (П.12.5)

Тогда давление

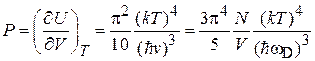, (П.12.6)

где учтено (4.69)

.

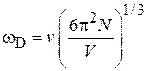Сравниваем с концентрацией фононов (П.12.3)

,

получаем

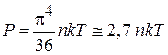. (П.12.7)

3.Для Z-валентного металла найти интервал температур, где теплоемкость электронного газа превышает теплоемкость кристаллической решетки.

Теплоемкость вырожденного газа NZ электронов согласно (П.10.19) равна

.

Теплоемкость кристаллической решетки, содержащей N узлов, при находим из закона Дебая (4.75)

.

Верхний край Т₁ искомого интервала удовлетворяет уравнению

,

,

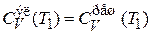откуда

. (П.12.8)

Учитывая , находим

.

При нормальной температуре электронный газ не дает существенного вклада в теплоемкость металла.

4.Найти теплоемкость графена при высоких и низких температурах.

В пленке графена существуют продольные и поперечные упругие волны с колебаниями в плоскости пленки, поэтому 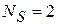. Если все точки и направления в пленке площадью S равноправны, то фазовый объем

,

где использовано приближение линейной дисперсии

,

v – средняя по двум типам волн скорость звука. Экспериментально получены (Nika D.L. at al. Phys. Rev. B79, 155413 (2009)): 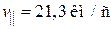, , 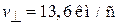тогда

дает 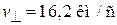. Используя (3.5)

,

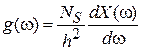находим плотность состояний

.

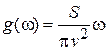Число независимых упругих волн равно числу степеней свободы пленки 2N, где N – число узлов двумерного кристалла. Для наибольшей частоты волн получаем уравнение

,

откуда находим частоту и температуру Дебая

,

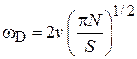. (П.12.9)

Для графена 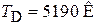, что превышает результат для алмаза 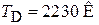более, чем в 2 раза. Тепловая часть внутренней энергии равна

.

Заменяя , получаем

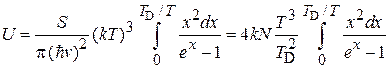. (П.12.10)

При высокой температуре верхний предел интеграла и x гораздо меньше единицы. Разлагаем экспоненту в ряд, находим внутреннюю энергию

и теплоемкость

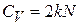(П.12.11)

– закон Дюлонга–Пти для двумерного кристалла.

При низкой температуре верхний предел интеграла (П.12.10) считаем бесконечным, тогда интеграл равен 2,404 и

.

Для теплоемкости кристаллической пленки при низких температурах получаем

(П.12.12)

– закон Дебая для двумерного кристалла.