Объединенное распределение. Полученные распределения (4.8), (4.10) и (4.12) объединяет формула

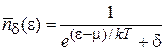, (4.13)

где

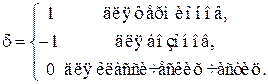
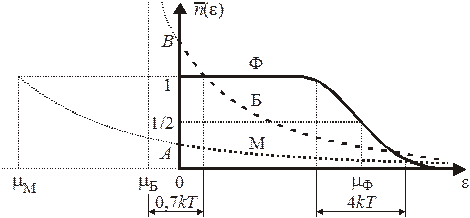
Распределения Максвелла(М),

Бозе–Эйнштейна (Б), Ферми–Дирака(Ф)

Квантовые распределения (4.8) и (4.10) переходят в классическое распределение (4.12) при

,

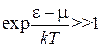тогда из

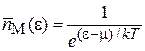
находим

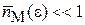, при .

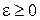Используя активность

,

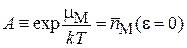для классической системы получаем

,

,

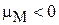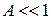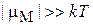. (4.14)

Химический потенциал системы.Если частица имеет сохраняющийся заряд – электрический, и/или барионный, и/или лептонный, то в силу закона сохранения заряда в изолированной системе число частиц сохраняется. Тогда химический потенциалопределяется из условия нормировки распределения на число частиц системы. Используем число частиц системы в интервале энергии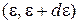

.

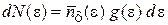Интегрируем по энергии, и получаем число частиц системы:

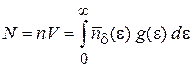, (4.15)

где n – концентрация частиц.

Для трехмерного газа с законом дисперсии 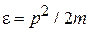плотность состояний (3.8а)

,

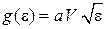где

.

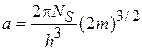Для распределения (4.13)

,

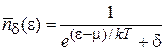получаем концентрацию

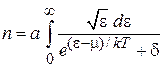. (4.16)

Следовательно, химический потенциал зависит от массы частицы m, от числа спиновых состояний N_S, от концентрации n, от температуры T и от рода газа .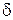

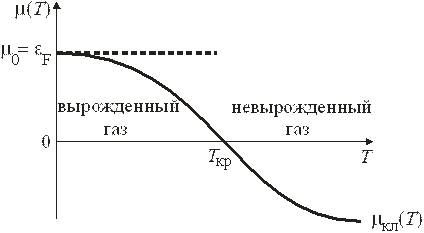
Зависимость химического потенциала трехмерного газа фермионов от температуры показана на рис.

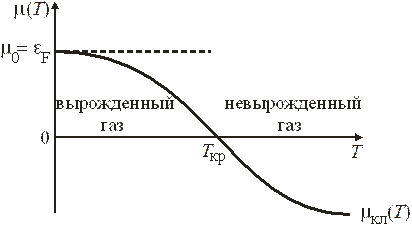
Критическая температура фермионов определяется условием

.

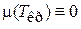Виды фермионного газа. В зависимости от температуры различают:

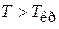– невырожденный газ, близкий к классическому газу;

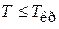– вырожденный газ с квантовыми свойствами.

Невырожденный газ описывается распределением Максвелла. Из (4.16) при 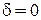получаем

,

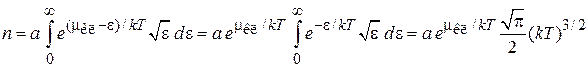где использовано

,

.

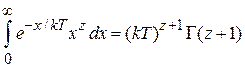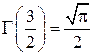Откуда выражаем активность и химический потенциал

,

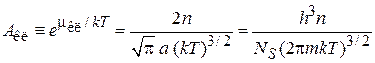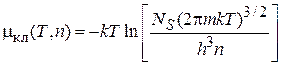. (4.17)

Химический потенциал невырожденного газа отрицательный, увеличивается с понижением температуры (как показано на рис.) и с ростом концентрации частиц. При 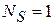результат совпадает с химическим потенциалом (2.62а) классического газа. Условия применимости классического распределения (4.14)

,

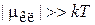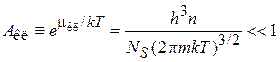(4.18)

выполняются, если:

· масса частицы m – большая;

· концентрация частиц n – мала;

· температура T – велика.

Вырожденный газ фермионов проявляет квантовые свойства и нарушает условия (4.18), тогда

, .

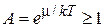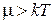Условия применимости квантового распределения:

· масса частицы мала;

· концентрация частиц велика;

· температура не превышает критического значения ;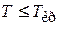

· ширина переходной области вблизи уровня Ферми мала по сравнению с энергией Ферми, тепловая энергия возбуждает незначительное количество из общего числа частиц.

Критическая температура фермионов. Используем

.

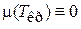Из (4.16)

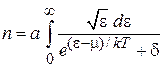
при 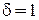, 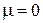получаем

.

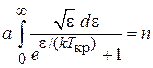Интеграл равен

,

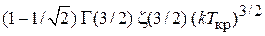где использовано

,

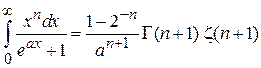тогда

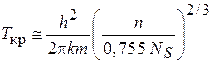. (4.19)

Для электронов ,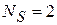

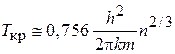. (4.19а)

Физический смысл критической температуры. Согласно распределению Максвелла наиболее вероятная скорость частицы

.

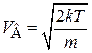Ей соответствует длина волны де Бройля при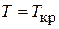

,

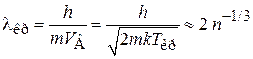где учтено (4.19а). Концентрацию частиц выражаем через среднее расстояние d между частицами

,

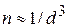тогда

.

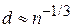С учетом 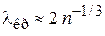получаем

.

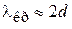При критической температуре длина волны де Бройля сравнима со средним расстоянием между частицами.

Для квантового газа фермионов:

· длина волны де Бройля велика по сравнению с расстоянием между частицами ;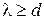

· температура газа низкая по сравнению с критической температурой ;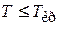

· ширина переходной области мала по сравнению с химическим потенциалом;

· тепловое движение активизирует малое число электронов, находящихся вблизи уровня Ферми.

Для классического газа фермионов:

· длина волны де Бройля мала ;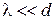

· температура газа высокая ;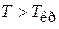

· ширина переходной области велика и сопоставима с максимальной энергией фермионов;

· все электроны активизированы тепловым движением;

· наиболее вероятный импульс большой.

Для электронного газа в металле

n » (1–18)×10²² см^–3, m » 10^–27 г.

Из (4.19а)

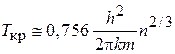
находим

.

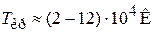При нормальной температуре получаем 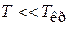и газ вырожден, доля активизированных электронов не превышает 1%. Это объясняет противоречие между классической теорией теплоемкости и экспериментом, показавшим, что электронный газ не дает вклада в теплоемкость металла.

Для собственного полупроводника

n £ 10¹⁷ см^–3, .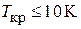

При нормальной температуре 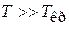, газ не вырожден, выполняется распределение Максвелла.

Молекулярный газ, например гелий с m » 3700 m_эл, остается невырожденным до очень низких температур.

Тепловые флуктуации числа частиц. Из (4.5) и (4.6) получаем

,

,

.

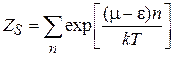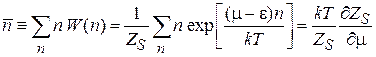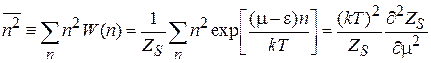Тогда дисперсия числа частиц

.

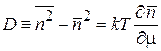Для универсального распределения (4.13)

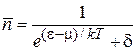
получаем

.

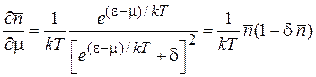В результате дисперсия числа частиц

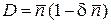. (4.20)

Для фермионов ,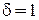

.

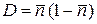Пр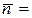и 0 и 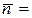1 получаем 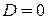, на уровне Ферми 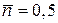и D_max = 0,25. Флуктуация фермионов не велика и максимальна на уровне Ферми.

Для бозонов ,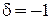

.

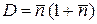При большой заселенности уровня 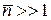дисперсия велика

.

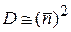Это объясняется взаимной интерференцией волновых пакетов, представляющих отдельные частицы и следующих в случайной последовательности. При интерференции двух волн с равными амплитудами наибольшая амплитуда удваивается, а интенсивность волны и плотность вероятности учетверяются. Наименьшая амплитуда и плотность вероятности равны нулю. В результате дисперсия числа частиц увеличивается. Интерференцией объясняется взаимное «притяжение» бозонов – при тепловом равновесии бозоны перемещаются группами. Фотонные пары с меньшим временным интервалом регистрируются чаще, чем пары с большим интервалом. Вероятность найти тождественные бозоны в близких квантовых состояниях выше, чем вероятность найти нетождественные частицы.

У фермионов перекрытие когерентных пакетов запрещено принципом Паули. Это приводит к взаимному «отталкиванию» фермионов и уменьшает флуктуацию числа частиц.

Корпускулярно-волновой дуализм бозонов. Из теории вероятности известно, что дисперсия аддитивна, если обусловлена независимыми причинами. Это имеет место для бозонов согласно

.

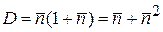Линейное слагаемое соответствует частицам, их флуктуация является дробовым шумом. Квадратичное слагаемое соответствует интерферирующим волнам, их флуктуация является волновым шумом. Наличие двух вкладов в дисперсию фотонов обнаружил А. Эйнштейн в 1909 г. Он рассматривал этот факт как проявление корпускулярно-волнового дуализма, т. е. совмещения волновых и корпускулярных свойств. При малой энергии, низкой частоте, большой длине волны заселенность состояний бозонов велика 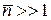, тогда 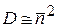и система проявляет волновые свойства. При большой энергии, большой частоте, малой длине волны заселенность мала 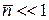, тогда 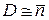и система проявляет корпускулярные свойства. Для классического идеального газа 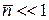, дисперсия мала 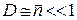. Флуктуация является дробовым шумом, газ проявляет корпускулярные свойства, и ведет себя как множество частиц.