Фазовая диаграмма однокомпонентной системы

Рассмотрим фазовую диаграмму однокомпонентной системы в самом общем виде. Математическое выражение правила фаз Гиббса, используемое в однокомпонентной (т.е. состоящей из одного компонента) системе имеет вид:

C = K – Ф + 2 = 1 – Ф + 2 = 3– Ф

Из этого уравнения следует, что если в системе в состоянии равновесия находится одна фаза, то вариантность системы равнаС = 2; если имеются две равновесные фазы, то вариантность равнаС = 1 и, наконец, если в системе в равновесии три фазы, то С = 0 .

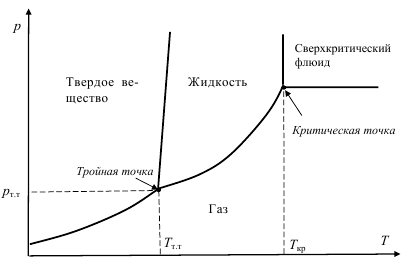
Рис. 3.9 Фазовая диаграмма однокомпонентной системы

Найдем соответствие вариантности системы и геометрического образа, отображающему такое состояние системы на фазовой диаграмме однокомпонентной системы. Типичный пример фазовой диаграммы, в которой существует одна твердая фаза, приведен на рис. 3.9.

Вариантность системы (число степеней свободы) равная двум соответствует такому геометрическому образу на фазовой диаграмме однокомпонентной системы, при котором можно произвольно (в определенных пределах) изменять значения двух переменных. В случае однокомпонентной системы эти переменные − давление и температура. При этом число равновесных фаз не изменится, это будет одна фаза. Следовательно, на плоской диаграмме этому состоянию соответствует образ − плоскость. На рис. 3.9 приведены четыре области, в каждой из которых в равновесии находится одна фаза: это область стабильного существования твердого вещества, область стабильного существования жидкости, область стабильного существования газа и область стабильного существования сверхкритического флюида. В каждой из этих областей до тех пор, пока мы не вышли за ее пределы, можно менять независимо друг от друга и давление и температуру, при этом число равновесных фаз не будет меняться. Если вариантность системы равна единице (число фаз в равновесии равно 2), это означает, что произвольно можно менять только одну переменную, а вторая будет менять функционально от нее. Такому состоянию равновесия двух фаз в системе на фазовой диаграмме соответствует линия. Это граничные линии между фазовыми областями. Случай, когда вариантность системы равна нулю (система безвариантна), возможен при равновесии трех фаз и этому состоянию соответствует геометрический образ −точка. Это тройная точка

При анализе фазовых диаграмм нужно иметь в виду, что если интересующая нас точка располагается на плоскости − значит в равновесии данной однокомпонентной системы находится одна фаза. Если интересующая нас точка попадает на линию – значит, в равновесии находятся две фазы и т.д.

Вопросы для самоконтроля

1. Приведите определение понятия «скорость химической реакции». Как на практике определяется скорость реакций? Связана ли скорость реакции с энергией Гиббса этой реакции? Почему скорость реакции определяется не вообще, а только на данный момент времени?

2. Почему в химической кинетике реакции подразделяются на гомогенные и гетерогенные? Приведите примеры тех и других реакций.

3. Почему в химической кинетике проводится классификация реакций на простые и сложные? Какие реакции называют последовательными, параллельными и цепными реакций? Можно ли по стехиометрическому уравнению определить, простая или сложная эта реакция?

4. Каков физико-химический смысл константы скорости реакции? Перечислите факторы, влияющие и не влияющие на константу скорости реакции.

5. Что нужно сделать для уменьшения скорости реакции? Дайте теоретическое обоснование ответа.

6. Объясните состояние химического равновесия с позиций химической термодинамики и химической кинетики.

7. Объясните физико-химический смысл константы химического равновесия.