Понятие о простой форме, комбинации и габитусе

На практических занятиях с лабораторными моделями в качестве простой формы рассматривается совокупность равных граней кристалла. Если все грани кристалла одинаковы, то он в целом является простой формой. Наоборот, если все грани кристалла не равны по форме и геометрическим очертаниям, то каждая из его граней является отдельной простой формой. Таким образом, в кристалле будет столько простых форм, сколько у него имеется геометрических типов граней, учитывая также их размеры. Например, в прямоугольном параллелепипеде 3 типа граней (рис.1).

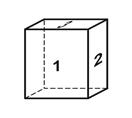
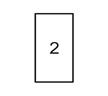
Рис.1. Типы граней в прямоугольном параллелепипеде

Следовательно, он состоит из 3 простых форм. Каждая из них, в свою очередь, состоит из 2 равных параллельных граней.

Названия простым формам даются в зависимости от числа граней и их взаимного расположения. Существует всего 47 простых форм, каждая из которых имеет свое название.

Для определения простых форм на практических занятиях необходимо равные между собой грани мысленно продолжить до их взаимного пересечения. Полученная при этом воображаемая фигура и будет искомой простой формой.

Среди простых форм различают два вида: открытые и закрытые. Грани открытой простой формы не замыкают пространство со всех сторон. Наоборот, грани закрытой простой формы при их взаимном продолжении в пространстве со всех сторон закроют какую-то его часть.

Сочетания простых форм, образующих кристаллы, называются сложными формами, или комбинациями. В комбинации будет столько простых форм, сколько в ней имеется типов граней. Одна открытая простая форма никогда не сможет образовать кристалл, она может встречаться только в комбинации с другими простыми формами. Комбинаций в природе - бесконечное количество.

Под габитусом кристалла понимается преобладающая по площади граней простая форма. Название габитуса совпадает с названием простой формы, но дается как определение (например, простая форма – куб, габитус – кубический). Если ни одна из простых по площади граней не преобладает (или трудно это оценить), габитус называется смешанным, или комбинированным.

Порядок разбора моделей кристаллов

При изучении моделей кристаллов на практических занятиях дается характеристика следующих данных:

1) формула симметрии кристалла;

2) сингония;

3) вид симметрии;

4) простые формы;

5) габитус.

Низшая категория сингоний

А. Триклинная сингония

Формулы и виды симметрии:

1) С – центральный вид симметрии;

2) примитивный вид симметрии.

Простые формы (рис.2.1-2.7):

1) пинакоид (пинакс – доска, греч.) – состоит из 2 равных параллельных граней (рис.2.1);

2) моноэдр (эдра – грань) – состоит из одной грани (это грань, которой нет ни одной равной во всем кристалле (рис.2.2).

Габитусы: пинакоидальный, моноэдрический.

Б. Моноклинная сингония

Формулы и виды симметрии:

1) L₂PC – планаксиальный вид симметрии,

2) L₂ – аксиальный вид симметрии,

3) Р – планальный вид симметрии.

Простые формы (рис. 2.1 – 2.7):

1) моноэдр (рис. 2.1);

2) пинакоид (рис. 2.2);

3) диэдр (рис. 2.3) – две равные, пресекающиеся при взаимном продолжении грани;

4) ромбическая призма – 4 равные грани, параллельные одному направлению, поперечное сечение фигуры – ромб (рис. 2.4).

Габитусы:

моноэдрический, пинакоидальный, диэдрический, ромбо-призматический и смешанный.

В. Ромбическая сингония

Формулы и виды симметрии:

1) 3L₂3PC – планаксиальный вид симметрии;

2) L₂2P – планальный вид симметрии;

3) 3L₂ – аксиальный вид симметрии.

Простые формы (рис. 2.1 – 2.7):

1) моноэдр (рис. 2.1);

2) пинакоид (рис. 2.2);

3) диэдр (рис. 2.3);

4) ромбическая призма (рис. 2.4);

5) ромбическая пирамида – четыре равные грани, пересекающиеся в одной точке (в поперечном сечении – ромб) (рис. 2.6);

6) ромбический тетраэдр – четыре равные грани, из которых каждые три пересекаются в одной точке (поперечное сечение через центр – ромб) (рис. 2.5);

7) ромбическая дипирамида – 8 равных граней, состоит как бы из двух равных пирамид (поперечное сечение – ромб) (рис.2.7).

Габитусы:

моноэдрический, пинакоидальный, диэдрический, ромбо-призматический, ромбо-пирамидальный, ромбо-дипирамидальный, ромбо-тетраэдрический и смешанный.

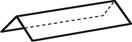
2.1 2.2 2.3

Моноэдр Пинакоид Диэдр;

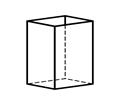
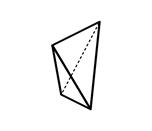
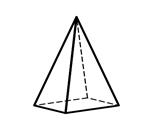
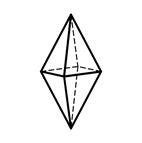
2.4 2.5 2.6 2.7

Ромбическая Ромбический Ромбическая Ромбическая

призма тетраэдр пирамида дипирамида

Рис.2. Простые формы низшей категории сингоний