Ферми-поверхность металлов

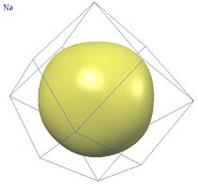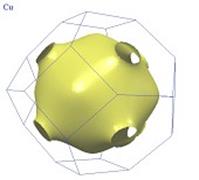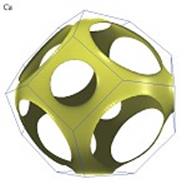Граница зоны Бриллюэна на рисунке имеет форму многогранника. Поверхность Ферми пересекает границу зоны Бриллюэна под прямым углом. Действительно, поверхность Ферми описывается уравнением 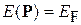. У границы зоны Бриллюэна групповая скорость электрона

,

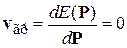поэтому электрон приближается к границе зоны Бриллюэна вдоль поверхности Ферми, следовательно, они взаимно перпендикулярны.

На границе зоны Бриллюэна одномерного кристалла в точках , где , групповая скорость равна нулю, и прилегающие участки кривых удовлетворяют , что соответствует поверхности Ферми.

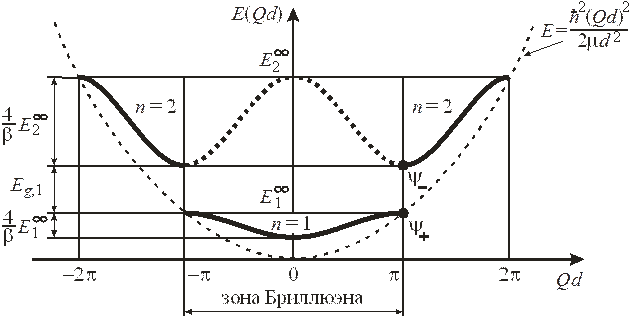
Внешнее электрическое поле E ускоряет электроны, что означает движение в импульсном пространстве. В результате поверхность Ферми смещается. Рассеяние электронов на примесях и дефектах кристаллической решетки изменяет их импульсы. Электроны с максимальным импульсом перебрасываются в свободные ячейки импульсного пространства, находящиеся около поверхности Ферми. В результате внешнее электрическое поле не изменяет радиуса сферы Ферми , но сдвигает ее центр на Dp. Согласно второму закону Ньютона,

,

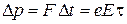где 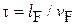– время релаксации импульса; l_F – длина свободного пробега электрона на уровне Ферми, движущегося со скоростью v_F. Вызванная полем плотность тока равна

,

где 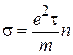– удельная электропроводность.

Средняя энергия электрона. Из (4.21)

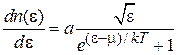
получаем вероятность того, что энергия электрона находится в интервале :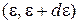

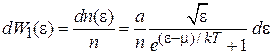, (4.26)

причем

.

Средняя энергия

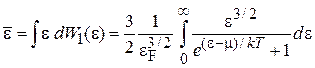. (4.27)

Внутренняя энергия и давление электронного газа при 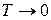. Используем (4.22)

,

,

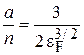получаем

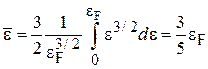. (4.28)

Внутренняя энергия газа из N электронов при абсолютном нуле вызвана принципом Паули и равна

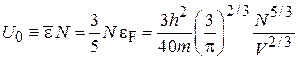. (4.29)

где учтено (4.22)

.

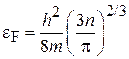Из (4.29) получаем давление

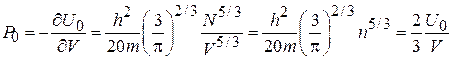. (4.30)

Давление электронного газа при абсолютном нуле температуры равно двум третям от внутренней энергии единицы объема, что совпадает с результатом для классического газа. Для золота

n = 5,9×10²² см^–3, P₀» 10¹¹ Па » 10⁶ атм.

Кроме металлов существуют другие объекты, где вырожденный газ фермионов определяет основные свойства вещества. Звезда «белый карлик» состоит из гелия плотностью ~10⁶ г/см³. Сильное гравитационное сжатие звезды отрывает атомные электроны от ядер и образуется электронный газ, давление которого противостоит сжатию. Масса такой звезды порядка массы Солнца, радиус порядка радиуса Земли. Расстояния между полностью ионизованными атомами d ~ 10^–2 Ǻ, что почти в 100 раз меньше, чем расстояние между атомами в молекуле водорода. Концентрация электронов, энергия Ферми, температура Ферми, температура звезды равны

n ~ 10³⁰ см^–3, e_F ~ 300 кэВ, T_F ~ 3×10⁹ К, T ~ 10⁷ К.

Выполняется 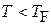, следовательно, электронный газ вырожден.

При дальнейшем росте массы гравитация сжимает звезду, концентрация электронного газа увеличивается. Протоны атомных ядер захватывают электроны, превращаясь в нейтроны. Давление газа, противостоящее сжатию, резко уменьшается из-за большой массы нейтрона и гравитация рывком сжимает звезду. Она взрывается, оболочка сбрасывается, появляется «сверхновая», или «нейтронная звезда». Давление вырожденного газа нейтронов

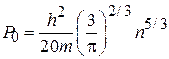
велико за счет выросшей концентрации нейтронов. Это давление противостоит гравитации. Масса такой звезды несколько больше массы Солнца, радиус, температура, концентрация и плотность равны

R ~ (20…30) км, T ~ 2×10⁶ К, n ~ 10³⁸ см^–3, r ~ 10¹⁴ г/см³.

Распределение Ферми–Дирака по энергии и по скорости. Для одно-, двух- и трехмерного электронного газа в металле число электронов с энергией в интервале 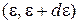равно

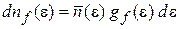, f = 1, 2, 3,

.

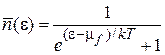С учетом двух проекций спина ранее получены числа состояний в единице f-мерного объема, в единичном интервале энергии для нерелятивистского газа

,

,

.

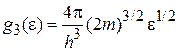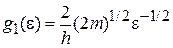Получаем распределения по энергии

,

,

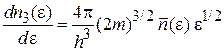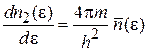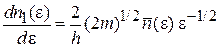. (4.31)

Выражение для 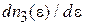совпадает с (4.21).

При 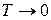используем

,

где – энергия Ферми, и находим концентрацию электронов

.

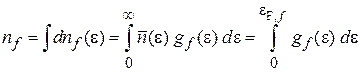Получаем

,

,

.

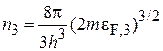Находим энергию Ферми

,

,

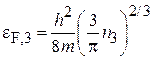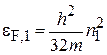. (4.32)

В распределении по энергии (4.31) выражаем энергию через скорость

, .

Получаем распределение Ферми–Дирака по модулю скорости – число частиц в единице объема с модулем скорости в единичном интервале около v

,

,

, (4.33)

где

.

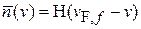Скорость Ферми 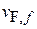находим из энергии Ферми (4.32) и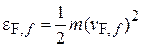

,

,

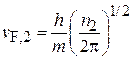. (4.34)

При низкой температуре распределения по модулю скорости (4.33) получают вид

,

,

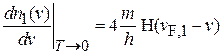. (4.35)

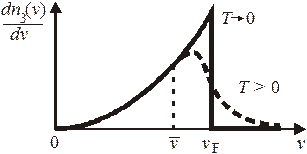
Распределение трехмерных электронов

по модулю скорости

Средняя скорость

,

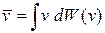определяется вероятностью

.

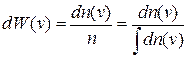Подставляем (4.35) и находим среднюю скорость

.

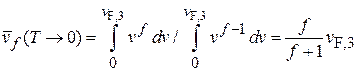Для серебра

, .

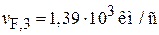Высокая скорость при абсолютном нуле вызвана принципа Паули.

Все направления в пространстве равноправные. Переходим от сферических и полярных координат к декартовым координатам

: ,

: .

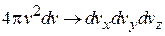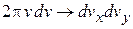Из (4.33) получаем распределение Ферми–Дирака по проекциям скорости

,

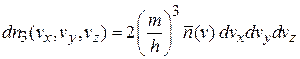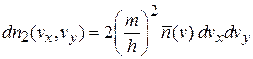, (4.36)

где

.

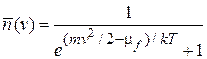Для трехмерного газа интегрируем (4.36) по поперечным к оси x составляющим и находим распределение Ферми–Дирака по одной из проекций скорости

(4.37а)

– число частиц в единице объема с проекцией скорости на ось x в единичном интервале около 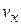. Здесь выполнено интегрирование по углу в плоскости и использовано

,

, ,

.

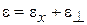При 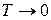используем

,

,

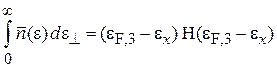получаем

. (4.38)

Для двухмерного газа из (4.36)

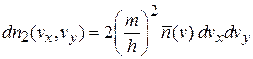
находим

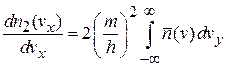. (4.37б)

При 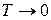используем

,

,

,

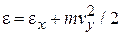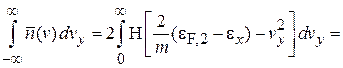
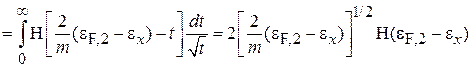где выполнена замена . В результате

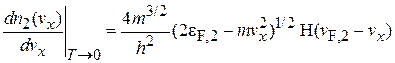. (4.39)

Одномерный газ при низкой температуре описывается распределением (4.35)

Контакт металлов

Приводим в контакт металлы 1 и 2, имеющие ограниченные размеры, близкие эффективные массы, и химические потенциалы . Энергетические зоны до установления термодинамического равновесия показаны на рис. а, где w – внутренняя контактная разность энергий. После момента контакта электроны начинают переходить между металлами. Система приходит в равновесие, когда выравниваются температуры и поток из металла 1 в металл 2 сравнивается с потоком электронов в обратном направлении.

а б

Контакт металлов до (а) и после (б) установления равновесия

За единицу времени через единицу площади из металла 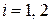уходит число электронов со скоростями в интервале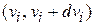

,

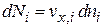где распределение Ферми по проекциям скорости (4.36)

.

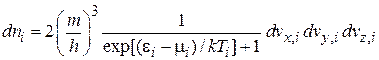Получаем

.

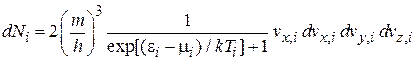При переходе поперечные скорости не меняются

, .

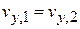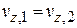Энергия электрона

сохраняется, тогда с учетом начала отсчета энергии на рис. а получаем

.

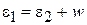Откуда следует соотношение между продольными скоростями

.

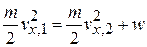Дифференцирование соотношений дает

, , .

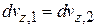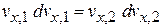При переходе к равновесию

, ,

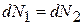химические потенциалы изменяются

.

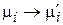Из 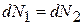в виде

,

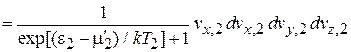с учетом предыдущих соотношений получаем

.

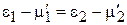Следовательно, расстояния от уровня энергии до уровней химического потенциала становятся одинаковыми в обоих металлах. В результате в состоянии равновесия соприкасающихся металлов уровни химических потенциалов выравниваются, как показано на рисунке б.

а б

Разность химических потенциалов

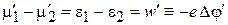
выражается через внутреннюю контактную разность потенциалов 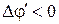. Для электрохимических потенциалов

,

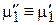получаем

.

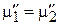Электрохимический потенциал одинаков во всех точках равновесной системы.

Электронный газ металлов вырожденный. Используем (4.22)

,

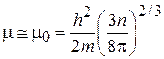находим внутреннюю контактную разность потенциалов

,

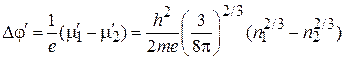где n_i – концентрация электронов проводимости. Металл 1, имеющий первоначально более высокий уровень Ферми, после установления равновесия заряжается положительно. Металл 2, у которого уровень Ферми был ниже, заряжается отрицательно. Между металлами возникает разность потенциалов.