Последовательное, параллельное

И СМЕШАННОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Последовательное соединение резисторов. Электрическая цепь может содержать несколько приемников электрической энергии, имеющих различные сопротивления. При расчете электрических цепей используют понятие «эквивалентное сопротивление» Rэкв.

Эквивалентным (или общим) называется такое сопротивлением,при включении которого в цепь вместо данной группы сопротивлений электрические условия всей остальной цепи остаются неизменными.

Пусть, например, внешняя цепь генератора (рис..6) состоит из трех приемников электрической энергии с сопротивлениями 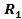. , . 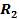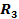Такое соединение приемников электрической энергии, при котором каждый из них поочередно включен в одну замкнутую электрическую цепь, называется последовательным. При этом

ток во всех приемниках одинаков, а сопротивление внешней цепи равно сумме сопротивлений приемников.

Для этого случая формула закона Ома имеет следующий вид:

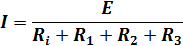
При наличии трех последовательно соединенных проводников общее сопротивление цепи составляет

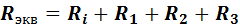
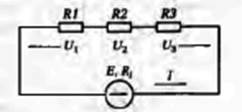
Рис..6. Последовательное соединение резисторов

Сопротивление внешней цепи

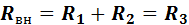
Напряжение на зажимах источника энергии равно напряжению, приложенному к внешней цепи

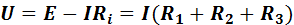
Напряжение на зажимах каждого из последовательно соединенных приемников энергии равно произведению тока на сопротивление этого приемника

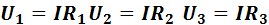
аобщеенапряжениеучасткацепи

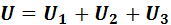
Таким образом, сумма напряжений на последовательно соединенных приемниках равна напряжению на зажимах источника энергии.

При неизменном напряжении ток зависит от сопротивления

цепи. Изменение сопротивления одного из последовательно включенных приемников влечет за собой изменение как общего сопротивления всей цепи, так и тока в ней.

Запомните

Последовательное включение добавочных резисторов используется на практике для понижения напряжения (пусковые и регулировочные реостаты), а также для расширения пределов измерения измерительных приборов, например вольтметров.

Параллельное соединение резисторов. Элементы электрической цепи, находящиеся под одним и тем же напряжением, называются параллельно соединенными. Припараллельном соединении резисторов (рис. 7) ток разветвляется по трем ветвям, тем самым уменьшая общее сопротивление или увеличивая общую проводимость цепи g:

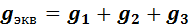
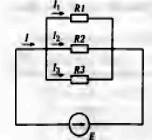
Рис. 7. Параллельное соединение резисторов

При этом

Так как проводимость есть величина, обратная сопротивлению, то общее сопротивление может быть записано в следующем виде:

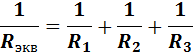
Установленное соотношение справедливо для любого числа параллельно соединенных резисторов.

В частном случае, если в электрической цепи содержатся два параллельно соединенных резистора R1 и R2, то можно написать следующее выражение для общего сопротивления:

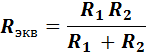
Если параллельно соединено какое-либо число п одинаковых резисторов R, то общее сопротивление такой цепи будет в п раз меньше сопротивления одного резистора:

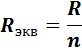
Для схемы рис..7 также будут справедливы следующие соотношения:

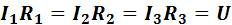
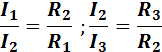
Эти соотношения указывают на то, что в цепях с параллельно включенными резисторами токи распределяются обратно пропорционально этим сопротивлениям или прямо пропорционально проводимостям этих проводников.

Таким образом, чем больше значение включенного параллельно резистора, тем меньше ток в нем, и наоборот.

Запомните

На практике параллельное включение резистора на участке электрической цепи используется для уменьшения тока на данном участке. В частности, такой параллельно включаемый резистор, называемый шунтом, применяется для расширения пределов измерения токов амперметрами. При наличии шунта в прибор ответвляется лишь часть измеряемого тока.

Смешанное соединение резисторов. Если в электрической цепи резисторы, соединенные параллельно между собой, включены последовательно с другими резисторами, то такое соединение их называется смешанным (рис. 8).

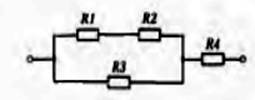
Рис. 8. Смешанное соединение

резисторов

При смешанном соединении резисторов определение общего, или эквивалентного, сопротивления 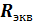в электрической цепи производится поэтапно. Например, для схемы рис..8 сначала определяется сопротивление Rn последовательно включенных резисторов

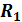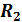и затем эквивалентное сопротивление 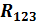, параллельно соединенных резисторов с сопротивлениям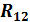и и 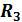а далее — эквивалентное сопротивление всей цепи .

+ ;

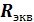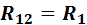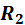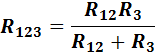
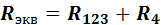
КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какое соединение приемников электрической цепи считается параллельным?

2. Чему равна сумма напряжений последовательно соединенных приемников?

3. Какое соединение резисторов называется смешанным?

ЗАКОНЫ КИРХГОФА

Для расчета сложных электрических цепей и определения их

электрического состояния применяют законы Кирхгофа, называемые в некоторых источниках также правилами Кирхгофа, которые были сформулированы Густавом Кирхгофом в 1845 г. Для сложных электрических цепей применяют понятия «ветвь»,

«узел» и «контур».

· Ветвь электрической цепи — это участок цепи, вдоль которого проходит один и тот же ток и который состоит из последовательно соединенных элементов (резисторов, источников ЭДС и т.д.).

· Узел электрической цепи -.это место соединения трех и более ветвей.

· Контур электрической цепи — это любой замкнутой путь, который можно обойти, перемещаясь по нескольким ее ветвям

Электрическая цепь, состоящая из трех ветвей, двух узлов и трех

контуров, дана на рис..9.

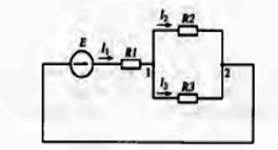
Рис.9.Электрическая схема.

Первый закон Кирхгофа (закон для токов) относится к узлам электрической цепи и формулируется так.

Алгебраическая сумма токов в узле электрической цепи в любой момент времени равна нулю:

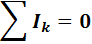
При этом токи, направленные к узлу, принимают со знаком «+», а токи, направленные от узла, — со знаком «-».

Запишем уравнение первого закона Кирхгофа для схемы рис. 9 (узла 1):

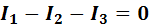
Для расчетов сложных электрических цепей с несколькими источниками энергии используют второй закон Кирхгофа, который может быть сформулирован следующим образом.

В замкнутом электрическом контуре алгебраическая сумма падений напряжений на участках цепи равна алгебраической сумме ЭДС, действующих в этом контуре:

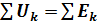или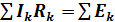

При составлении уравнений слагаемые берут со знаком «+», если действующие на участках напряжения и ЭДС совпадают с направлением обхода, и со знаком «-», если их действия противоположны направлению обхода.

Для схемы рис. 9 запишем уравнения по второму закону Кирхгофа для трех контуров

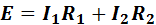
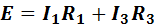
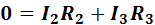
При включении в электрическую цепь источников электрической энергии, ЭДС которых совпадают по направлению (рис. 10, а), ЭДС всей цепи равна сумме ЭДС этих источников (согласное включение):

+ +….

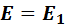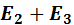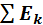
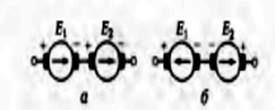
Рис. 10. Включение источников питания:

а - согласное; б — встречное

Если же в цепи ЭДС источников имеют противоположные направления (рис. 10, б), то результирующая ЭДС равна разности ЭДС этих источников (встречное включение):

-….

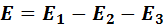При составлении уравнений необходимо выбрать направления обхода цепи и произвольно задаться направлениями токов.Расчет сложной электрической цепи с несколькими ЭДС производят с помощью уравнений 1-го и 2-го законов Кирхгофа в следующем порядке.

1. Условно задаются направлениями токов на различных участках цепи.

2. Определяют число уравнений, которое необходимо составить для решения задачи. Если известны все ЭДС и сопротивления цепи, число уравнений должно быть равно числу неизвестных токов.

3. Составляют уравнения с помощью уравнений 1-го закона Кирхгофа. Число уравнений по 1 -му закону Кирхгофа на единицу меньше числа узлов электрической схемы. Остальные уравнения составляют по 2-му закону Кирхгофа.

4. Намечают независимые контура, направления обхода этих контуров и приступают к составлению уравнений по 2-му закону Кирхгофа. Если направления обхода не совпадают с направлениями ЭДС или направлениями токов на отдельных участках контура, то величины ЭДС и падения напряжения записывают в уравнении со знаком «-».

5. Решают полученную систему уравнений. Если в результате решения уравнений некоторые из токов получились отрицательными, То это означает, что направление токов было выбрано неправильно. Необходимо изменить направление токов на схеме.

6- Проверяют правильность решения путем подстановки полученных значений токов в одно из составленных уравнений.

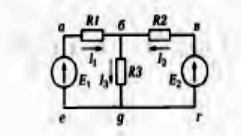
Пример 3. Электрическая цепь, проведенная на рисунке, имеет следующие параметры:

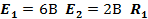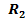=2Ом =4Ом 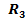=5Ом.Определить тoки во всех ветвях схемы.

Решение

Произвольно выбираем направление токов в ветвях цепи. Для узла б записываем уравнение 1-го закона Кирхгофа:

+

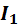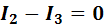
Для контура а —б—д —еи контура а — в —г — е составляем уравнения 2-го закона Кирхгофа:

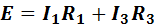
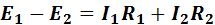
Таким образом, имеем три независимых уравнения с тремя неизвестными. Подставляем числовые значения в эти уравнения и решаем их:

+

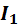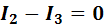
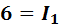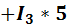
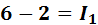*2

*2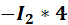

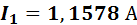
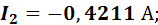
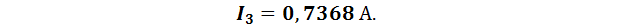
Знак «-» показывает, что действительное направление тока 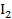обратно принятому направлению. Проведем проверку, подставив полученные значения токов в уравнение 1го закона Кирхгофа:

1,1578 - 0,4211 - 0,73688 = 0.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется узлом, ветвью и контуром электрической цепи?

2. В чем состоит суть 1 -го и 2-го законов Кирхгофа? Сформулируйте их.

3. Как необходимо выбрать направления обхода электрической цепи при составлении уравнений?

4. Какое включение в электрическую цепь источников электрической

энергии называется согласным, а какое — встречным ?