Возможность и направление протекания ОВР

Для установления возможности самопроизвольного протекания в стандартных условиях ОВР помимо расчета ЭДС, можно воспользоваться нахождением ∆G⁰₂₉₈ для этой реакции. Отрицательное значение ∆G⁰₂₉₈ как и положительное значение ЭДС, свидетельствует о том, что в стандартных условиях при 298 К эта реакция может протекать самопроизвольно, без подвода энергии извне.

При обратимом осуществлении ОВР в условиях р = const и V= const изменение энергии Гиббса будет равно электрической работе Аэл., совершаемой системой.

∆G⁰ = - Аэл.

Потенциал ОВ пары вычисляют по уравнению Нериста, которое можно представить в виде

Е=Е₀ + 0,059 a окиссл.

N lg a восст.

ЭДС = Е⁰_окисл. – Е⁰_восст.; С_исх./ С_{прод .}= 1/К

В состоянии равновесия активности реагентов и продуктов приобретут равные значения и ЭДС станет равной нулю, а выражение под знаком логарифма 1/К, тогда ln1/K = ln1 - lnK; ln1=0

O = ΔE⁰+(R · T/ n· F) · ln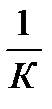

ΔЕ⁰- (R · T/n · F) · lnK

или +n ∙ F · Δ E⁰ = RT · lnK

- n· F · ΔE⁰ = Δ G

В соответствии со II законом термодинамики самопроизвольно протекают только процессы имеющие Δ G<0, то реакция ОВР идет слева направо, только если ЭДС>0.

ΔGp = -RT· lnK = -nF· ΔE⁰

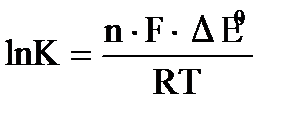
Если взаимодействует сильный окислитель с сильным восстановителем, то происходит односторонний процесс. Он практически протекает до конца, т.к. его продуктами обычно является соединения со слабо выраженными окислительно–восстановительными свойствами. При малом отличии окислительно–восстановительной активности исходных веществ и продуктов реакции процесс является двусторонним. Для количественной оценки направленности процессов пользуются значениями G⁰ реагентов и продуктов реакции, а для частного случая ОВР, протекающих в разбавленных водных растворах при t=25⁰С, 101кПа можно пользоваться значениями нормальных электродных потенциалов.

Сопоставляя электродные потенциалы соответствующих систем,, можно заранее определять направление в котором будет протекать ОВР.

Стандартная э.д.с. Е⁰ гальванического элемента связана со стандартной энергией Гиббса ∆ G⁰ протекающей в элементе реакции соотношением.

∆G⁰=-nF· ∆E⁰

С другой стороны ∆G⁰ связана с константой равновесия К реакции уравнением.

n ·F·ΔE⁰ = 2,3 · RT · lgK

lgK = n ∙F · Δ E⁰ / 2,3 RT

lgK = n ∙ Δ E⁰ / 0,059

Эту работу можно предоставить как количество переменного в ходе этого процесса электричества nF (n – число электронов, переходящих от восстановителя к окислителю в элементарном акте реакции, F – постоянная Фарадея), умноженнае на разность потенциалов Е между электродами соответствующего гальванического элемента.

ΔG= - n· F · Δ E

Для ОВР при Т = 298 ΔG⁰= - n ·F · ΔE⁰

При условиях, отличающихся от стандартных, для системы

Ox + ne↔Redэлектродный потенциалопределяется уравнением Нернста

E_oх/Red = E⁰_0х/Red - (RT/n· F) · ln(C(Red)/С(Ox))

E_ox/Red и E⁰_ox/Red - электродный и стандартный потенциалы системы.

n – число электронов, участвующих в процессе.

C(Red) и C_ox молярные концентрации восстановленной и окисленной форм.

E_ox/Red = E⁰_ox/Red – (0,059/n) · lg C(Red)/С(Ox)

или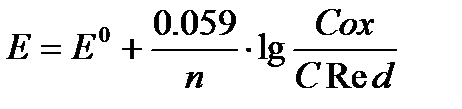

Например :

для системы MnO₄^- + 8H⁺ + 5e ↔ Mn²⁺ + 4H₂O

E MnO^-₄/ Mn²⁺ = 1,51 – (0,059/5) · lg (C_Mn²⁺/С_MnO^-_{4 ·} C_(H+)⁸)

Пример:

Выбрать галогенид калия в качестве восстановителя для FeCl₃

2KГ^- + 2 Fe ³⁺Cl_3(P) = Г⁰₂ + 2KCl_(P) + 2 Fe ²⁺Cl_2(P)

(Г = F^-, Cl^-, Br^-, I^- )

По таблице: E⁰_Fe3+/Fe+2 = +0,77B

E⁰_F2/2F- = + 2,86B

E⁰_Cl2/2Cl- = + 1,36B

E⁰_Br2/2Br- = +1,07B

E⁰_I2/2I- = +0,54B < 0.77 B

Вычислим э.д.с. с участием гологенидов для KI

ΔЕ⁰₂₉₈ = Е⁰_окисл. – Е⁰_восст. = 0,77 – 0,54 = 0,23В > 0. Только иодид калия будет