Расчет оптимальных параметров реактора периодического действия
Курс, рус. отд., осенний семестр, 2015-2016 уч. год
Расчёт задачи №1 на оптимальный температурный режим химико-технологического процесса, оптимальных параметров реактора периодического действия (задание индивидуальное)
Оптимальный температурный режим химико-технологического процесса
Химико-технологические расчеты составляют главную, наиболее трудоемкую часть проекта любого химического производства. Цель этих расчетов определение кинетических констант, оптимальных параметров процесса, вычисление реакционных объемов и основных размеров химических реакторов.
Температурный (тепловой) режим проведения химического процесса, обеспечивающий экономически целесообразную максимальную производительность единицы объема реактора (интенсивность) по целевому продукту, называют оптимальным.
Подход к разработке оптимального температурного режима может быть различным в зависимости от типа химической реакции. Максимальная интенсивность реактора будет достигнута при проведении процесса с максимально возможной скоростью. В случае эндотермической реакции интенсивность растет с ростом температуры, в случае экзотермической реакции зависимость интенсивности и эффективности реакции от температуры не линейная. Поэтому для нахождения оптимальной температуры, а с ней связаны и другие параметры реакционного процесса (равновесная и максимальная степени превращения, среднее время пребывания реагентов в зоне реакции и ряд других), необходим совокупный анализ кинетического уравнения, зависимости конечной и равновесной степеней превращения от констант химической реакции, температур и времени пребывания, а также их взаимного влияния. Решение поставленной задачи аналитическим методом либо очень сложно, либо не представляется возможным, поэтому для нахождения оптимальных параметров химико-технологического процесса на основе экзотермической химической реакции используем графоаналитический метод решения.
Расчет оптимальных параметров реактора периодического действия
Расчет оптимальных параметров химико-технологического процесса для реакции типа 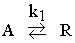
1. Определение оптимальной температуры и максимальной степени превращения
1.1. Зависимость степени превращения от кинетических параметров реакторного процесса (k1, t , x Ae)
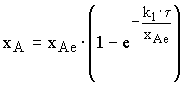 ,
,
где 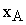 - степень превращения вещества А;
- степень превращения вещества А; 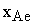 - равновесная степень превращения вещества А;
- равновесная степень превращения вещества А; 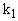 - константа скорости прямой реакции, с-1.
- константа скорости прямой реакции, с-1.
1.2. Зависимость скорости прямой реакции от температуры
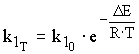 ,
,
где 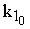 - предэкспоненциальный множитель; R - универсальная газовая постоянная, 8310 Дж/кг·К; DЕ - энергия активации прямой реакции, Дж/кмоль.
- предэкспоненциальный множитель; R - универсальная газовая постоянная, 8310 Дж/кг·К; DЕ - энергия активации прямой реакции, Дж/кмоль.
1.3. 3ависимость равновесной степени превращения от константы равновесия
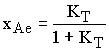 ,
,
где 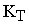 - константа равновесия при температуре T.
- константа равновесия при температуре T.
1.4. Зависимость константы равновесия от температуры
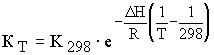 ,
,
где 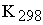 - константа равновесия при 298 К; DН - тепловой эффект реакции, Дж/кмоль.
- константа равновесия при 298 К; DН - тепловой эффект реакции, Дж/кмоль.
1.5. Табулируем KT, 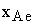 ,
, 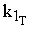 ,
, 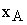 по температуре в диапазоне от 240 до 400 К с шагом 20 К (табл. 9).
по температуре в диапазоне от 240 до 400 К с шагом 20 К (табл. 9).
Таблица 9 - Результаты расчета степени превращения в реакторе
| Температура, К | Константа равновесия, KT | Равновесная степень превращения 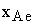 | Константа скорости прямой реакции  ,с-1 ,с-1 | Степень превращения 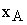 |
| Тi | 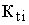 | 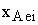 | 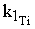 | 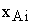 |
По результатам расчета строим график зависимости 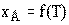 (рис. 8).
(рис. 8).
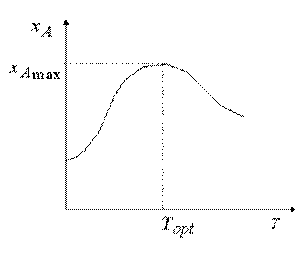 Рис. 8.Зависимость степени превращения вещества А от температуры Рис. 8.Зависимость степени превращения вещества А от температуры | 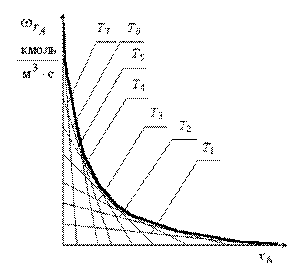 Рис. 9.Линия оптимальных температур Рис. 9.Линия оптимальных температур |
2. Определение времени химико-технологического процесса при проведении его по линии оптимальных температур.
2.1. Определение зависимости скорости реакции от степени превращения
( 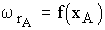 ) при температуре Т.
) при температуре Т.
Зависимость вида 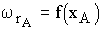 определяем на основе уравнения
определяем на основе уравнения
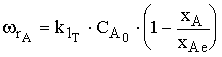 ,
,
где 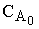 - начальная концентрация вещества А, кмоль/м3.
- начальная концентрация вещества А, кмоль/м3.
При Т = const данное уравнение описывает прямую пересекающую ось абсцисс в точке 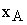 =
= 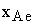 (значение
(значение 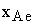 из табл. 9) и ось ординат в точке
из табл. 9) и ось ординат в точке 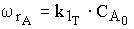 (значение
(значение 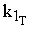 из табл. 9).
из табл. 9).
2.2. Построение линии оптимальных температур
Линию оптимальных температур определяем графическим способом, она представляет собой огибающую к совокупности линий 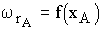 во всем диапазоне температур (рис. 9).
во всем диапазоне температур (рис. 9).
2.3. Среднее время пребывания при проведении процесса по линии оптимальных температур, с
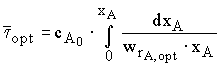 ,
,
где 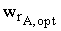 - скорость химической реакции соответствующая линии оптимальных температур (определяется по рис. 9),
- скорость химической реакции соответствующая линии оптимальных температур (определяется по рис. 9), 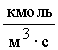 .
.
Решение данного уравнения проводим численным методом, для чего табулируем 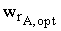 по
по 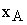 от 0 до
от 0 до 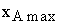 с шагом
с шагом 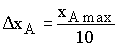 (табл. 10).
(табл. 10).
Таблица 10 - Данные для расчета 
| № п/п | 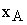 | 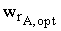 , , 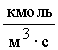 | 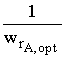 , , 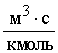 |
| i | 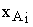 | 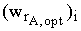 | 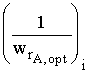 |
Среднее время пребывания определяем по формуле трапеций, с
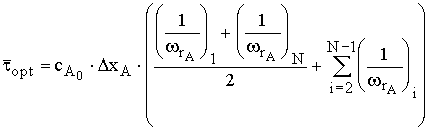 ,
,
где N - число строк в табл. 10.
3. Прирост производительности реактора при проведении процесса по линии оптимальных температур, %
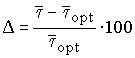 .
.
Задача 1. Обратимую экзотермическую реакцию первого порядка 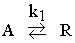 проводят в реакторе идеального вытеснения. Процесс характеризуется следующими параметрами:
проводят в реакторе идеального вытеснения. Процесс характеризуется следующими параметрами: 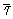 - среднее время пребывания, с; DH - тепловой эффект реакции, Дж/кмоль;
- среднее время пребывания, с; DH - тепловой эффект реакции, Дж/кмоль; 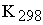 - константа равновесия при 298 К;
- константа равновесия при 298 К; 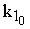 - предэкспоненциальный множитель; DЕ - энергия активации прямой реакции, Дж/кмоль; Т - температура проведения процесса, К;
- предэкспоненциальный множитель; DЕ - энергия активации прямой реакции, Дж/кмоль; Т - температура проведения процесса, К; 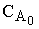 - начальная концентрация вещества А, кмоль/м3.
- начальная концентрация вещества А, кмоль/м3.
Возможны два температурных режима проведения процесса: при поддержании в реакторе одинаковой температуры и в соответствии с линией оптимальных температур.
Требуется определить: 1) оптимальную температуру, обеспечивающую максимальную степень превращения при проведении процесса по первому варианту при принятом 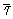 ; 2) время проведения процесса по линии оптимальных температур до той же степени превращения, что и при проведении процесса в оптимальных условиях по первому варианту.
; 2) время проведения процесса по линии оптимальных температур до той же степени превращения, что и при проведении процесса в оптимальных условиях по первому варианту.
Исходные данные по вариантам приведены в табл. 1.
Таблица 1 - Данные для расчета оптимальных параметров химико-технологического процесса
| № п/п | 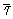 , с , с | DH·10-6, Дж/кмоль | 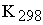 | 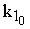 ·10-5 ·10-5 | DЕ·10-6, Дж/кмоль | 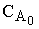 , кмоль/м3 , кмоль/м3 |
| -62 | 15,5 | 0,8 | 0,9 | |||
| -64 | 0,9 | 39,5 | 0,95 | |||
| -72 | 1,3 | 45,5 | 1,15 |
