Расчет коэффициентов теплоотдачи от стенки к жидкости

3.5.1 Коэффициент теплоотдачи от стенки к жидкости определяется из критериальных уравнений конвективной теплоотдачи.

Коэффициент теплоотдачи входит в критерий Нуссельта [2-7]

, (15)

где – критерий Нуссельта;

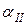– коэффициент теплоотдачи, Вт/(м²×К);

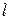– определяющий геометрический размер, м,

; (16)

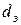– эквивалентный диаметр, м;

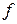– площадь сечения потока жидкости, м²;

– полный смоченный периметр сечения потока, м;

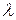– коэффициент теплопроводности жидкости, Вт/(м×К).

При вынужденном движении жидкости (газа) в трубках и каналах конкретный вид критериального уравнения для определения критерия Нуссельта зависит от режима движения жидкости (газа).

Режим движения характеризуется значением критерия Рейнольдса

, (17)

где 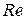– критерий Рейнольдса;

– скорость движения жидкости, м/с;

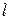– определяющий геометрический размер, м;

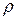– плотность жидкости, кг/м³;

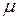– динамический коэффициент вязкости жидкости, Па×с;

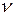– кинематический коэффициент вязкости жидкости, м²/с.

3.5.2 В случае развитого турбулентного режима движения жидкости в прямых трубах и каналах ( ) критерий Нуссельта определяется по уравнению [2-7]

, (18)

где – поправочный коэффициент, учитывающий влияние на коэффициент теплоотдачи отношения длины труб теплообменника к их диаметру; при ;

– критерий Прандтля, рассчитанный для жидкости при средней температуре ,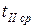

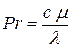, (19)

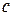– удельная теплоемкость жидкости, Дж/ (кг×К);

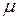– динамический коэффициент вязкости жидкости, Па×с;

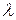– коэффициент теплопроводности жидкости, Вт/(м×К);

– критерий Прандтля, рассчитанный для жидкости при температуре стенки.

Значения критерия Прандтля для различных жидкостей при различных температурах 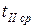приведены на рисунке 6 [4].

В критериальные уравнения конвективной теплоотдачи входит отношение , учитывающее направление теплового потока. У капельных жидкостей с увеличением температуры величина критерия Прандтля уменьшается, следовательно, при нагревании жидкостей 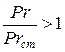, а при охлаждении жидкостей . При проектировании теплообменников в расчете коэффициента теплоотдачи для нагревающихся жидкостей допускается принимать , а для охлаждающихся жидкостей можно принимать среднее

значение .

Вещество	Точка	Вещество	Точка	Вещество	Точка
Амилацетат		Изопропиловый спирт		Толуол
Аммиак, 26%		Йодистый этил		Уксусная кислота, 100%
Анилин		Ксилол		Уксусная кислота, 50%
Ацетон		Метиловый спирт, 100%		Хлорбензол
Бензол		Метиловый спирт, 40%		Хлороформ
Бромистый этил		Октан		Четыреххлористый углерод
Бутиловый спирт		Пентан
Вода		Серная кислота, 111%		Этилацетат
Гептан		Серная кислота, 98%		Этиленгликоль
Диэтиловый эфир		Серная кислота, 60%		Этиловый спирт, 100%
Глицерин, 50%		Сероуглерод		Этиловый спирт, 50%
Изоамиловый спирт		Соляная кислота, 30%

Рисунок 6 – Значения критерия Прандтля для жидкостей

Для газов уравнение для расчета критерия Нуссельта упрощается, так как , а критерий Прандтля зависит от атомности газов [5]:

– одноатомные газы 0,67;

– двухатомные газы 0,72;

– трехатомные газы 0,8;

– четырех- и многоатомные газы 1,0,

например, для воздуха критериальное уравнение принимает вид [2-5]:

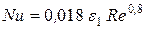. (20)

3.5.3 При ламинарном режиме движения жидкости в прямых трубах и каналах ( 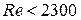) критерий Нуссельта можно определить по следующим уравнениям [3,4,7]:

, (21)

или [2]

, (22)

а также [5]

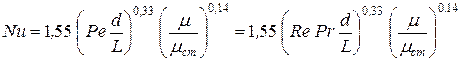, (23)

где 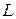– длина трубы, м;

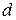– диаметр трубы, м;

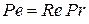– критерий Пекле;

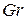– критерий Грасгофа,

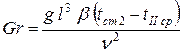; (24)

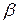– коэффициент объемного расширения жидкости (газа), К^-1.

3.5.4 При теплоотдаче в переходном режиме движения жидкости 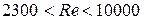критерий Нуссельта определяется из графической зависимости. График зависимости приведен на рисунке 7 [5].

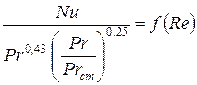
или

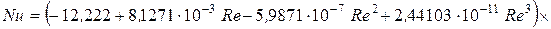
, (25)

а также по приближенному уравнению

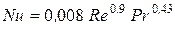. (26)

Рисунок 7 – Зависимость критерия Нуссельта

от критерия Рейнольдса при переходном режиме