С активным, индуктивным и емкостным

СОПРОТИВЛЕНИЯМИ

При расчетах цепей переменного тока, так же как и цепей постоянного тока, используют законы Ома и Кирхгофа. Отличие в применении этих законов заключается в том, что в цепях переменного тока необходимо учитывать углы сдвига фаз между токами и напряжениями.

Цепь переменного тока, в которую включены последовательно активное сопротивление R, индуктивность L, обладающая индуктивным сопротивлением 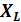, и емкость С, имеющая емкостное сопротивление, 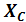изображена на рис. .8, а.

Под действием переменного напряжения и в этой цепи протекает переменный ток iСогласно закону Ома определим падения напряжения на каждом элементе цепи:

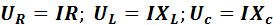
Эти падения напряжения имеют соответствующие углы сдвига фаз по отношению к общему току цепи I.

Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. .8,б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали в выбранном масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения 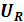откладываем по вектору токаI . Напряжение на индуктивности опережает ток на угол = 90°. 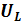Поэтому вектор откладываем вверх под углом 90° к вектору тока I . 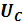В цепи семкостьюи наоборот, напряжение отстает от тока на угол = 90°, поэтому вектор откладываем на диаграмме вниз под углом 90° к вектору тока I.

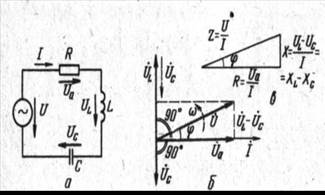
Рис. .8. Цепь переменного тока с последовательно включенными сопротивлением ,индуктивностью и емкостью:

а — электрическая схема; б — векторная диаграмма; в — треугольник сопротивлений

Для определения общего напряжения, приложенного к зажимам

цепи, сложим векторы 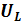и. 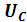Для этого вычтем из большего вектора 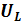и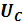

вектор 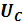и получим вектор ( 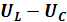,) выражающий векторную сумму этих двух напряжений. Теперь сложим векторы ( ) .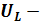

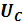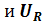Суммой этих векторов будет диагональ параллелограмма — вектор Uявляющийся общим напряжением на зажимах цепи:

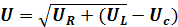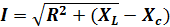²или ²

Полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления,

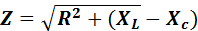²

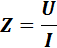
Полная проводимость цепи:

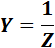
Угол сдвига фаз между током и напряжением цепи определяется тригонометрическими функциями:

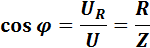
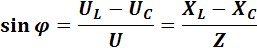
Если 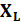>, 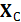то вектор напряжения U опережает вектор тока I, а если 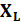< 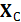то Uотстает от тока I.Треугольник сопротивлений изображен на рис..8, в

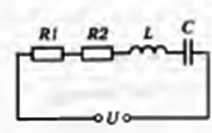
Пример .4. В электрическую цепь, приведенную на рисунке, с напряжением U = 220 В последовательно включены: резистор с активным сопротивлением 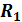, = 5 Ом, индуктивная катушка Lс активным сопротивлением

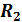= 3 Ом и индуктивным сопротивлением 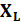= 4 Ом, конденсатор С с емкостным сопротивлением 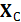= 10 Ом. Определить ток в цепи и напряжение на отдельных элементах цепи. Нарисовать векторную диаграмму.

Решение

Определяем общее сопротивление

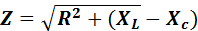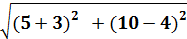² = =10Ом

Ток в цепи

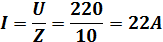
Напряжение на отдельных элементах цепи:

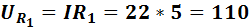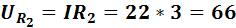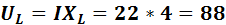В

В

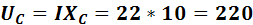В

В

Векторная диаграмма приведена на рисунке ниже.

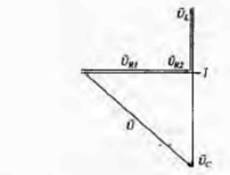
Рассмотрим электрическую цепь, состоящую из двух приемников, подключенных параллельно к зажимам источника синусоидального напряжения u= 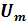sin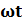

(рис. .9,а). В первом приемнике включены последовательно элементы 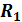и L, во втором соответственно 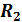и С. Оба приемника находятся под действием одного общего напряженияu. Запишем выражения для мгновенных значений токов для первой и второй ветви:

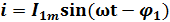
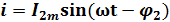
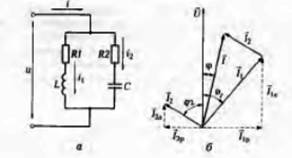
Рис. 9. Цепь переменного тока с параллельно соединенными элементам

а — электрическая схема: б — векторная диаграмма

Так как в первую ветвь включена индуктивная катушка, а во вторую— конденсатор, то электрические цепи соответственно носят индуктивны й и емкостной характер.

Действующее значение тока I и косинус угла определяем из следующих выражений:

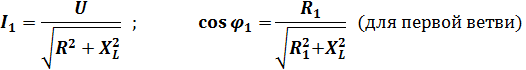
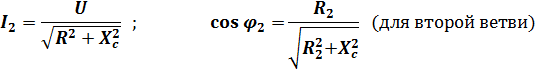
Значение тока I в неразветвленной части цепи определяют как геометрическую сумму токов в ветвях, т.е.I = +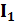

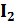
Векторная диаграмма приведена на рис. 9, б. Токи, протекающие через ветви, состоят из активной 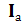и реактивной 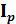составляющих и соответственно имеют индуктивный и емкостной характер.

Ветвь с активной составляющей характеризуется активной проводимостью

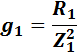
Ветвь с реактивной составляющей характеризуется реактивной проводимостью 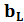. Для первой ветви реактивная проводимость

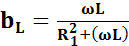₂

Реактивная проводимость 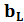не является величиной, обратной реактивному сопротивлению, так как при ее определении учитывается и активное сопротивлении ветви. Полная проводимость ветви

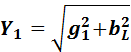
КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие законы используют при расчете цепей переменного тока?

2.В чем состоит принципиальное отличие расчета цепей переменного

тока от расчета цепей постоянного тока?

РЕЗОНАНС НАПРЯЖЕНИЙ

В цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, соединенными последовательно (рис. 10, а), может возникнуть резонанс напряжений

Резонанс напряжений наступает в том случае, если индуктивное сопротивление 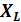и емкостное сопротивление 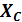равны между собой, т.е.

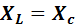
Так как эти сопротивления зависят от частоты, резонанс наступает при определенной резонансной частоте :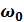

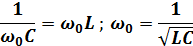
При заданной частоте 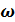резонанс напряжений может быть достигнут изменением L и С.

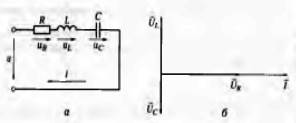
Рис. 10. Цепь переменного тока при резонансе напряжения:

а — электрическая схема; б — векторная диаграмма

Когда цепь не настроена в резонанс, ее полное сопротивление

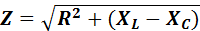²

При резонансе напряжений в рассматриваемой цепи, когда 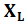= 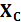ее полное сопротивление

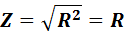
Запомните

1. Полное сопротивление цепи при резонансе напряжений равно активному сопротивлениюR.

2. Угол сдвига фаз между током и напряжением при резонансе равен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи сактивным сопротивлением)

Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает. Напряжение генератора переменного тока, включенного в цепь, расходуется на активном сопротивлении:

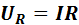
Напряжение на индуктивности и емкости определяется согласно закону Ома. В связи стем что в последовательно соединенных сопротивлениях протекает одинаковый ток и при резонансе индуктивное сопротивление 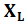= 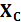напряжения на индуктивности и емкости тоже равны:

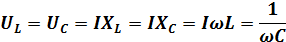
Векторная диаграмма для рассматриваемой цепи при резонансе напряжения приведена на рис 10, б. На векторной диаграмме видно, что напряжения на индуктивности и емкости равны, сдвинуты по фазе друг относительно друга на 180° и взаимно компенсируются.

Если одновременно увеличить оба реактивных сопротивления 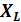и 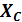, не нарушая при этом условия резонанса 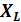=, 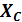то соответственно возрастут оба частичных напряжения 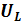и, 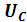а сила тока в цепи при этом не изменится. Таким образом, можно получить 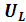и 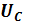во много раз большие, чем напряжение U на зажимах цепи, поэтому резонанс напряжений — опасное явление для энергетических установок.

В электроустановках большой мощности резонанс напряжений, который может наступить внезапно, например при изменении емкостного сопротивления, может привести к опасным перенапряжениям и рассматривается как аварийный. В технике связи и автоматике явление резонанса напряжений широко используют для настройки приемных и передающих устройств на определенную частоту

Пример.5. В цепь переменного тока включены последовательно активное сопротивление R = 3 Ом, индуктивность L= 0,005 Гн и емкость С = 63,5 мкф. Генератор, включенный в цепь, вырабатывает переменное напряжение U = 2,5 В с резонансной частотой 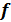= 285 Гц. Определить индуктивное и емкостное сопротивления, полное сопротивление цепи, токпротекающий в цепи, напряжения на емкости и индуктивности.

Решение

Индуктивное сопротивление

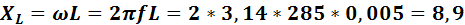Ом

Емкостное сопротивление

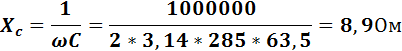
Индуктивное сопротивление равно емкостному, следовательно, в цепи наступает резонанс напряжения.

Полное сопротивление цепи при резонансе напряжения

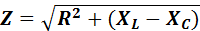² = 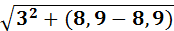² = 3Ом

Сила тока в цепи

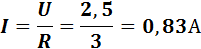
Напряжение на индуктивности

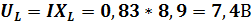
Напряжение на емкости

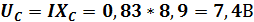
Как видно из представленного примера, в режиме резонанса напряжения на индуктивности и емкости равны и превышают напряжение генератора.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется резонансом напряжений?

2. Чему равно полное сопротивление цепи при резонансе напряжений?

3. Чему равен угол сдвига фаз между током и напряжением при резонансе напряжений?

4. Какую опасность представляет резонанс напряжений в технике?

РЕЗОНАНС ТОКОВ

В цепи переменного тока, в которой индуктивность L, емкость Си сопротивлениеR соединены параллельно (рис. .11, а), может возникнуть резонанс токов при условии равенства реактивных сопротивлений:

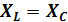
Ток при резонансе достигает минимального значения I = U/R, a cos = 1, т. е. достигает своего максимального значения.

Значение резонансной частоты определяется формулой

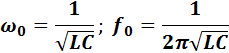
Из формулы следует, что, изменяя величину емкости или индуктивности контура, можно изменять (регулировать) частоту свободных колебаний, т. е. настраивать контур на определенную частоту.

Векторная диаграмма изображена на рис..11, б в режиме резонанса токов.

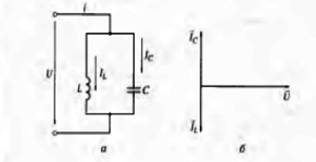
Рис .11. Цепь переменного тока при резонансе тока:

а-электрическая схема; б — векторная диаграмма

Свободные электрические колебания, возникающие в колебательном контуре, всегда затухающие. Затухание колебаний в контуре объясняется тем, что при прохождении электрического то в контуре энергия тратится на нагревание провода, из которого изготовлены индуктивная катушка и соединительные провода.

Потеря энергии в контуре вызывает постепенное уменьшение амплитуды свободных колебаний и их полное прекращение. Скорость затухания колебаний в контуре связана с потерей энергии в нем и зависит от сопротивления контура.

Запомните

■ Токи в ветвях, содержащих L и С, при резонансе тока могут быть

больше общего тока цепи.

■ Индуктивный и емкостной токи противоположны по фазе, равны по значению и по отношению к источнику энергии взаимно

компенсируются, т. е. идет обмен энергией между индуктивной

катушкой и конденсатором.

■ Реактивная мощность цепи при резонансе токов равна нулю, поскольку равны и противоположно направлены токи 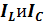. Иными словами, реактивная мощность, потребляемая в индуктивной катушке, равна реактивной мощности, генерируемой в конденсаторе.

В результате резонанса токов общий ток в цепи может быть относительно мал, а в ветвях индуктивности и емкости, где происходят электрические колебания, переменный ток значительно больше общего.

Пример 6. Разветвленная цепь, приведенная на рисунке слева, имеет

следующие параметры: 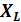= = 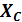10 Ом, R = 40 Ом, U= 120 В. Определить токи в ветвях и общий ток цепи. Построить векторную диаграмму.

Решение

Определим токи в ветвях:

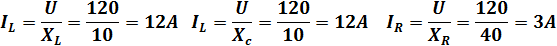
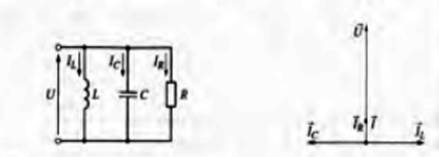
Рассчитаем общий ток цепи

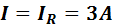
Векторная диаграмма изображена на рисунке справа. Общий ток цепи при резонансе токов в четыре раза меньше тока в ветвях, содержащих реактивные элементы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. При каких условиях возникает резонанс токов?

2. От чего зависит скорость затухания колебаний в контуре?

3. Чему равна реактивная мощность цепи при резонансе токов?