Основные свойства кристаллов

Тема Симметрия твердых тел

1 Кристаллические и аморфные тела.

2 Элементы симметрии и их взаимодействия

3 Симметрия кристаллических многогранников и кристаллических решеток.

4 Принципы построения кристаллографических классов

Лабораторная работа № 2

Изучение структуры моделей кристаллов

Приборы и принадлежности: карточки с указанием химических элементов, имеющих кристаллическую структуру;

Цель работы: изучить кристаллические и аморфные тела, элементы симметрии кристаллических решеток, принципы построения кристаллографических классов, вычислить период кристаллической решетки для предложенных химических элементов.

Основные понятия по теме

Кристаллы – твердые тела, обладающие трехмерной периодической атомной структурой. При равновесных условиях образования имеют естественную форму правильных симметричных многогранников. Кристаллы – равновесное состояние твердых тел.

Каждому химическому веществу, находящемуся при данных термодинамических условиях (температура, давление) в кристаллическом состоянии, соответствует определенная атомно-кристаллическая структура.

Кристалл, выросший в неравновесных условиях и не имеющий правильной огранки или потерявший ее в результате обработки, сохраняет основной признак кристаллического состояния – решетчатую атомную структуру (кристаллическую решетку) и все определяемые ею свойства.

Кристаллические и аморфные твердые тела

Твердые тела чрезвычайно разнообразны по структуре своего строения, характеру сил связи частиц (атомов, ионов, молекул), физическим свойствам. Практическая потребность в тщательном изучении физических свойств твердых тел привела к тому, что примерно половина всех физиков на Земле занимается исследование твердых тел, созданием новых материалов с наперед заданными свойствами и разработкой их практического применения. Известно, что при переходе веществ из жидкого состояния в твердое возможны два различных вида затвердевания.

Кристаллизация вещества

В жидкости, охлажденной до определенной температуры, появляются кристаллики (области упорядоченно расположенных частиц) – центры кристаллизации, которые при дальнейшем отводе тепла от вещества растут за счет присоединения к ним частиц из жидкой фазы и охватывают весь объем вещества.

Затвердение вследствие быстрого повышения вязкости жидкости с понижением температуры.

Твердые тела, образующиеся при таком процессе затвердения, относятся к аморфным телам. Среди них различают вещества, у которых кристаллизация совсем не наблюдается (сургуч, воск, смола), и вещества, способные кристаллизоваться, например, стекло. Однако, вследствие того, что вязкость у них быстро растет с понижением температуры, затрудняется перемещение молекул, необходимое для формирования и роста кристаллов, и вещество успевает затвердеть до наступления кристаллизации. Такие вещества называются стеклообразными. Процесс кристаллизации этих веществ, протекает очень медленно в твердом состоянии, причем более легко, при высокой температуре. Известное явление "расстекловывания" или "затухания" стекла обусловлено образованием внутри стекла мелких кристалликов, на границах которых происходит отражение и рассеяние света, вследствие чего стекло становится непрозрачным. Похожая картина имеет место при "засахаривании" прозрачного сахарного леденца.

Аморфные тела можно рассматривать как жидкости с очень большим коэффициентом вязкости. Известно, что у аморфных тел можно наблюдать слабо выраженное свойство текучести. Если наполнить воронку кусками воска или сургуча, то через некоторое время, разное для различных температур, куски аморфного тела будут постепенно расплываться, принимая форму воронки и вытекать из нее в виде стержня. Даже у стекла обнаружено свойство текучести. Измерения толщины оконных стекол в старых зданиях показали, что за несколько веков стекло успело стечь сверху вниз. Толщина нижней части стекла оказалась немного большей верхней.

Строго говоря, твердыми телами следует назвать только кристаллические тела. Аморфные тела по некоторым свойствам, а главное по строению, аналогичны жидкостям: их можно рассматривать как сильно переохлажденные жидкости, имеющие очень большую вязкость.

Известно, что в отличие от дальнего порядка в кристаллах (упорядоченное расположение частиц сохраняется по всему объёму каждого кристаллического зерна), в жидкостях и аморфных телах наблюдается ближний порядок в расположении частиц. Это значит, что по отношению к любой частице, расположение ближайших соседних частиц является упорядоченным, хотя и выражено не так чётко, как в кристалле, но при ударении от данной частицы, расположение по отношению к ней других частиц, становится все менее упорядоченным и на расстоянии 3-х – 4 - х эффективных диаметров молекулы, порядок в расположении частиц полностью исчезает.

Сравнительные характеристики различных состояний вещества приведены в таблице 2.1.

Кристаллическая решетка

Для удобства описания правильной внутренней структуры твердых тел обычно пользуются понятием пространственной или кристаллической решетки. Она представляет собой пространственную сетку, в узлах которой располагаются частицы – ионы, атомы, молекулы, образующие кристалл.

На рисунке 2.1 изображена пространственная кристаллическая решетка. Жирными линиями выделен наименьший параллелепипед, параллельным перемещением которого вдоль трех координатных осей, совпадающих с 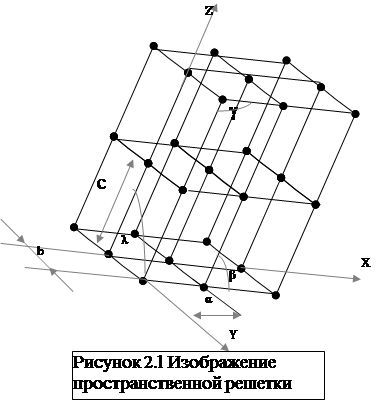направлением ребер параллелепипеда, может быть построен весь кристалл. Этот параллелепипед называется основной или элементарной ячейкой решётки. Атомы расположены в данном случае в вершинах параллелепипеда.

Для однозначной характеристики элементарной ячейки задается 6 величин: три ребра a, b, c и три угла между ребрами параллелепипеда a, b, g.Эти величины называются параметрами решетки. Параметры a, b, c – это межатомные расстояния в кристаллической решётке. Их численные значения порядка 10^-10 м.

Простейшим типом решёток являются кубические с параметрами a=b=c и a = b = g= 90⁰.

Индексы Миллера

Для символического обозначения узлов, направлений и плоскостей в кристалле используются так называемые индексы Миллера.

Индексы узлов

Положение любого узла в решётке относительно выбранного начала координат определяется тремя координатами X, Y, Z (рисунок 2.2).

Через параметры решетки эти координаты можно выразить следующим образом X= ma, Y= nb, Z= pc, где a, b, c – параметры решётки, m, n, p – целые числа.

Таким образом, если за единицу длин вдоль оси решетки взять не метр, а параметры решётки a, b, c (осевые единицы длины), то координатами узла будут числа m, n, p. Эти числа называются индексами узла и обозначаются .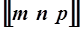

Для узлов, лежащих в области отрицательных направлений координат, ставиться над соответствующим индексом знак минус. Например .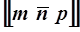

Индексы направления

Для задания направления в кристалле выбирается прямая, (рисунок 2.2) проходящая через начало координат. Её ориентация однозначно определяется индексом m n p первого узла, через который она проходит. Следовательно, индексы направления определяются тремя наименьшими целыми числами, характеризующими положение ближайшего от начала координат узла, лежащего на данном направлении. Индексы направления записывают следующим образом .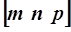

Рисунок 2.3 Основные направления в кубической решетке.

Семейство эквивалентных направлений обозначается ломаными скобками .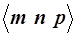

Например, семейство эквивалентных направлений 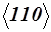включает направления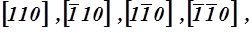

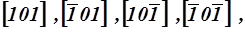
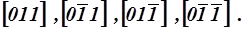
На рисунке 2.3 представлены основные направления в кубической решетке.

Индексы плоскости

Положение любой в пространстве определяется заданием трех отрезков ОА, ОВ, ОС (рисунок 2.4), которые она отсекает на осях выбранной системы координат. В осевых единицах длины отрезков будут: ; ; .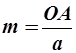

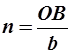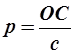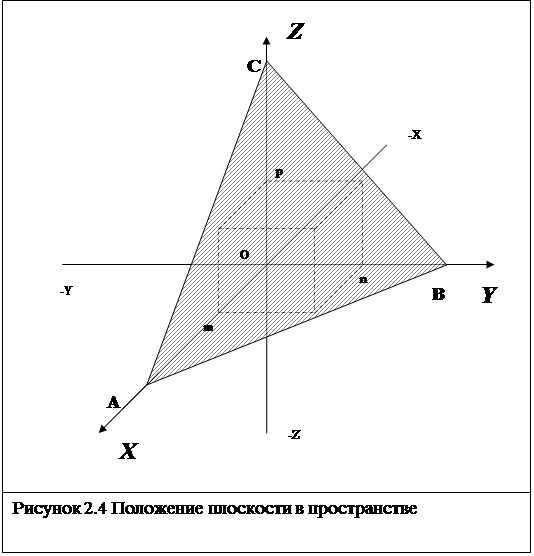Три числа m n p вполне определяют положение плоскости S. Для получения Миллеровских индексов с этими числами нужно сделать некоторые преобразования.

Составим отношение обратных величин осевых отрезков 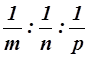и выразим его через отношение трех наименьших чисел h, k, l так, чтобы выполнялось равенство .

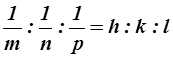Числа h, k, l являются индексами плоскости. Для нахождения индексов плоскости отношение 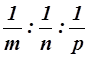приводят к общему наименьшему знаменателю и знаменатель отбрасывают. Числители дробей и дают индексы плоскости. Поясним это на примере: m = 1, n = 2, p = 3. Тогда 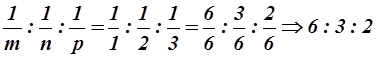. Таким образом, для рассматриваемого случая h = 6, k = 3, l = 2. Миллеровские индексы плоскостей заключаются в круглые скобки (6 3 2).Отрезки m n p могут быть и дробными, но индексы Миллера и в этом случае выражаются целыми числами.

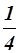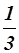Пусть m =1, n = , p = , то .

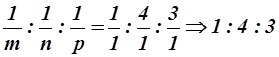При параллельной ориентации плоскости относительно какой-нибудь оси координат, индекс, соответствующий этой оси, равен нулю.

Если отрезок, отсекаемый на оси, имеет отрицательное значение, то соответствующий индекс плоскости тоже будет иметь отрицательный знак. Пусть h = - 6 , k = 3, l = 2, то такая плоскость в Миллеровских индексах плоскостей запишется .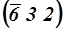

Необходимо отметить, что индексы плоскости (h, k, l) задают ориентацию не какой-то конкретной плоскости, а семейства параллельных плоскостей, то есть, по существу, определяют кристаллографическую ориентацию плоскости.

На рисунке 2.5 изображены основные плоскости в кубической решетке.

Некоторые плоскости, отличающиеся по индексам Миллера, являются

эквивалентными в физическом и кристаллографическом смысле. В кубической решетке одним из примеров эквивалентности являются грани куба 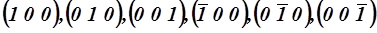. Физическая эквивалентность состоит в том, что все эти плоскости обладают одинаковой структурой в расположении узлов решетки, а следовательно, и одинаковыми физическими свойствами. Кристаллографическая эквивалентность их в том, что эти плоскости совмещаются друг с другом при повороте вокруг одной из осей координат на угол, кратный .Семейство эквивалентных плоскостей задается фигурными скобками. Например символом 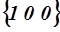обозначается все семейство граней куба.

Трехкомпонентная символика Миллера применяется для всех систем решеток, кроме гексагональной. В гексагональной решетке (рисунок 2.7 №8) узлы расположены в вершинах правильных шестигранных призм и в центрах их шестиугольных оснований. Ориентация плоскостей в кристаллах гексагональной системы описывается с помощью четырех осей координат х₁ , х₂ , х₃ , z, так называемыми индексами Миллера – Браве. Оси х₁ , х₂ , х₃ расходятся из начала координат под углом 120⁰ . Ось z перпендикулярна к ним. Обозначение направлений по четырёхкомпонентной символике затруднительно и применяется редко, поэтому направления в гексагональной решётке задаются по трехкомпонентной символике Миллера.

Основные свойства кристаллов

Одним из основных свойств кристаллов является анизотропия. Под этим термином понимается изменение физических свойств в зависимости от направления в кристалле. Так кристалл может иметь для разных направлений различную прочность, твердость, теплопроводность, удельное сопротивление, показатель преломления и т.д. Анизотропия проявляется и в поверхностных свойствах кристаллов. Коэффициент поверхностного натяжения для разнородных граней кристалла имеет различную величину. При росте кристалла из расплава или раствора это является причиной различия скоростей роста разных граней. Анизотропия скоростей роста обуславливает правильную форму растущего кристалла. Анизотропия поверхностных свойств также имеет место в различии адсорбционной способности скоростей растворения, химической активности разных граней одного и того же кристалла. Анизотропия физических свойств является следствием упорядоченной структуры кристаллической решетки. В такой структуре плотность упаковки атомами плоскостей различна. Рисунок 2.6 поясняет сказанное.

Расположив плоскости в порядке убывания плотности заселения их атомами, получим следующий ряд: (0 1 0) (1 0 0) (1 1 0) (1 2 0) (3 2 0) . В наиболее плотно заполненных плоскостях атомы прочнее связаны друг с другом, так как расстояние между ними наименьшее. С другой стороны, наиболее плотно заполненные плоскости, будучи удаленными друг от друга на относительно большие расстояния, чем малозаселённые плоскости, будут слабее связаны друг с другом.

На основании изложенного можно сказать, что наш условный кристалл легче всего расколоть по плоскости (0 1 0), чем по другим плоскостям. В этом и проявляется анизотропия механической прочности. Другие физические свойства кристалла (тепловые, электрические, магнитные, оптические) также могут быть различными по разным направлениям. Важнейшим свойством кристаллов, кристаллических решёток и их элементарных ячеек является симметрия по отношению к определённым направлениям (осям) и плоскостям.

Симметрия кристаллов

Таблица 2.1

Кристаллическая система	Соотношение ребер элементарной ячейки	Соотношение углов в элементарной ячейке
Триклинная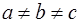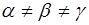
Моноклинная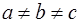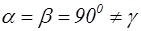
Ромбическая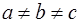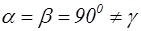
Тетрагональная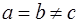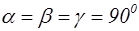
Кубическая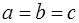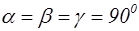
Тригональная (робоэдрическая)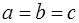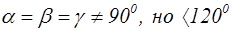
Гексагональная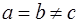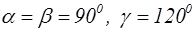

В силу периодичности расположения частиц в кристалле он обладает симметрией. Это свойство заключается в том, что в результате некоторых мысленных операций система частиц кристалла совмещается сама с собой, переходит в положение не отличаемое от исходного. Каждой операции можно поставить в соответствие элемент симметрии. Для кристаллов существует четыре элемента симметрии. Это – ось симметрии, плоскость симметрии, центр симметрии и зеркально-поворотная ось симметрии.

В 1867 году русский кристаллограф А.В. Гадолин показал, что может существовать 32 возможные комбинации элементов симметрии. Каждая из таких возможных комбинаций элементов симметрии называется классом симметрии. Опытом было подтверждено, что в природе существуют кристаллы, относящиеся к одному из 32 классов симметрии. В кристаллографии указанные 32 класса симметрии в зависимости от соотношения параметров а, в, с, a, b, g объединяют в 7 систем(сингоний), которые носят следующие названия: Триклинная, моноклинная, ромбическая, тригональная, гексагональная, тетрагональная и кубическая системы. В таблице 2.1 приведены соотношения параметров для указанных систем.

Как показал французский кристаллограф Браве всего существует 14 типов решеток, принадлежащих различным кристаллическим системам.

Если узлы кристаллической решетки расположены только в вершинах параллелепипеда, представляющего собой элементарную ячейку, то такая решетка называется примитивной или простой( рисунок2.7№№ 1, 2, 4, 9, 10, 12), если, кроме того, имеются узлы в центре оснований параллелепипеда, то такая решетка называется базоцентрированной ( рисунок2.7№№ 3, 5), если есть узел в месте пересечения пространственных диагоналей, то решетка называется объемоцентрированной ( рисунок2.7№№ 6, 11, 13), а если имеются узлы в центре всех боковых граней – гранецентрированной (рисунок2.7№№ 7, 14). Решетки, элементарные ячейки которых содержат дополнительные узлы внутри объема параллелепипеда или на его гранях, называются сложными.

Решетка Браве представляет собой совокупность одинаковых и одинаково расположенных частиц (атомов, ионов), которые могут быть совмещены друг с другом путем параллельного переноса. Не следует полагать, что одна решетка Браве может исчерпать собой все атомы (ионы) данного кристалла. Сложную структуру кристаллов можно представить как совокупность нескольких реше 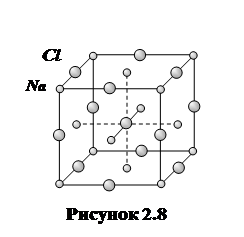ток Браве, вдвинутых одна в другую. Например, кристаллическая решетка повареной соли NaCl ( рисунок 2.8) состоит из двух кубических гранецентрированных решеток Браве, образованных ионами Na ^– и Cl ⁺, смещенных относительно друг друга на половину ребра куба.

Вычисление периода решетки.

Зная химический состав кристалла и его пространственную структуру, можно вычислить период решетки этого кристалла. Задача сводиться к тому, чтобы установить число молекул (атомов, ионов) в элементарной ячейке, выразить ее объем через период решетки и, зная плотность кристалла, произвести соответствующий расчет. Важно отметить, что для многих типов кристаллической решетки большинство атомов принадлежит не одной элементарной ячейке, а входит одновременно в состав нескольких соседних элементарных ячеек.

Для примера определим период решетки хлористого натрия, решетка которого показана на рисунке 2.8.

Период решетки равен расстоянию между ближайшими одноименными ионами. Это соответствует ребру куба. Найдем число ионов натрия и хлора в элементарном кубе, объем которого равен d³, d – период решетки. По вершинам куба расположено 8 ионов натрия, но каждый из них является одновременно вершиной восьми смежных элементарных кубов, следовательно, данному объему принадлежит лишь 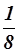часть иона, расположенного в вершине куба. Всего таких ионов натрия весемь, которые в совокупности составляют 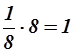ион натрия. Шесть ионов натрия расположены в центрах граней куба, но каждый из них принадлежит рассматриваемому кубу только наполовину. В совокупности они составляют 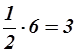иона натрия. Таким образом, рассматриваемому элементарному кубу принадлежит четыре иона натрия.

Один ион хлора расположен на пересечении пространственных диагоналей куба. Он целиком принадлежит нашему элементарному кубу. Двенадцать ионов хлора размещены по серединам ребер куба. Каждый из них принадлежит объему d³ на одну четверть, так как ребро куба одновременно является общим для четырех смежных элементарных ячеек. Таких ионов хлора рассматриваемому кубу принадлежит 12, которые в совокупности составляют 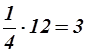иона хлора. Всего в элементарном объеме d³ содержится 4 иона натрия и 4 иона хлора, то есть 4 молекулы хлористого натрия (n = 4).

Если 4 молекулы хлористого натрия занимают объем d³, то на один моль кристалла придется объем 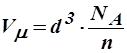, где 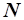_А – число Авогадро, n – число молекул в элементарной ячейке.

С другой стороны 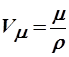, где 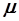- масса моля, 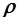- плотность кристалла. Тогда 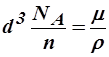откуда

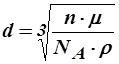(2.1)

При определении числа атомов в одной параллелепипедной элементарной ячейке (подсчет содержания) нужно руководствоваться правилом:

q если центр атомной сферы совпадает с одной из вершин элементарной ячейки, то от такого атома данной ячейке принадлежит 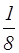, так как в любой вершине параллелепипеда одновременно сходятся восемь смежных параллелепипедов, к которым в равной мере относится вершинный атом (рисунок 2.9);

q от атома, расположенного на ребре ячейки принадлежит данной ячейке 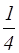, так как ребро является общим для четырех параллелепипедов (рисунок 2.9);

q 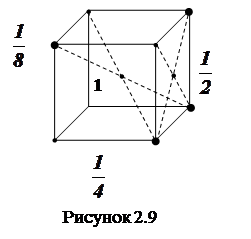от атома, лежащего на грани ячейки, принадлежит данной ячейке 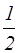, так как грань ячейки общая для двух параллелепипедов (рисунок 2.9);

q атом, расположенный внутри ячейки, принадлежит ей целиком (рисунок 2.9).

При использовании указанного правила форма параллелепипедной ячейки безразлична. Сформулированной правилом может быть распространено на ячейки любых систем.

Ход работы

У полученных моделей реальных кристаллов

1 Выделить элементарную ячейку.

2 Определить тип решетки Браве.

3 Произвести "подсчет содержания" для данных элементарных ячеек.

4 Определить период решетки .

5 Изобразить на рисунке плоскости и направления по индексам Миллера, указанным преподавателем.

6 Отчет по лабораторной работе содержит ответы на все пункты.

Вопросы для самоконтроля

1 Основные свойства кристаллических и аморфных тел.

2 Для чего вводятся индексы Миллера?

3 Основные классы симметрии.