Регуляция путем изменения биосинтеза ферментов

В настоящее время установлено, что синтез и распад ферментов, как и других белков, происходит в организме непрерывно. У взрослого здорового человека в условиях динамического равновесия процессы синтеза и распада имеют одинаковую скорость, благодаря чему общее содержание фермента не изменяется во времени. Для каждого фермента характерна своя скорость распада. В большинстве случаев полное прекращение синтеза фермента привело бы к исчезновению 50% молекул фермента за несколько дней, но некоторые ферменты обновляются значительно быстрее. Скорость синтеза фермента может варьировать от нуля до максимума, тогда как скорость распада представляется постоянной.

Вещество, которое избирательно препятствует синтезу определенного фермента, называется репрессором. При помощи механизма репрессии конечные продукты реакций обмена веществ могут регулировать процесс их собственного образования по принципу обратной связи. Было доказано, что в некоторых системах накопление метаболитов, образующихся в итоге цепи последовательных реакций, предотвращает синтез одного из ферментов, функционирующего в начале этой цепи (Рис 5. 11). Продукт реакции в таком случае действует как специфический репрессор синтеза этого фермента.

Рисунок 5.11 – Регуляция синтеза фермента. Конечный продукт (Г) цепи метаболических реакций снижает концентрацию фермента, катализирующего этап Б→В путем репрессии его синтеза.

Теоретическое часть

Кинетика ферментативных реакций

Уже в ранних исследованиях по влиянию концентрации реагента на скорость ферментативных реакций была обнаружена очень важная особенность ферментативного катализа, которая заключается в сложном характере кинетики этих реакций. Так, при низких концентрациях реагента (или субстрата) реакция протекает в соответствии с уравнением первого порядка. При высоких концентрациях субстрата скорость перестает зависеть от концентрации и, таким образом, реакция в этих условиях протекает в соответствии с уравнением нулевого порядка. Общий вид зависимости скорости ферментативной реакции от концентрации субстрата при такой двухступенчатой кинетике приведен на Рис. 6.1. При высоких концентрациях субстрата весь фермент оказывается связанным с субстратом, и скорость реакции будет максимальной. Другими словами, в реакциях, катализируемых ферментами, стадией, определяющей скорость процесса, будет стадия распада комплекса на фермент и продукт.

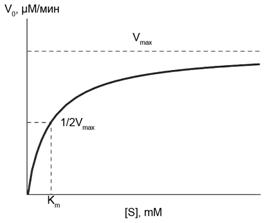
Рисунок 6.1 – Зависимость скорости ферментативной реакции от концентрации субстрата.

Итак, начальная скорость ферментативной реакции, обозначенная на Рис. 6.1 символом V₀ (скорость, измеряемая за период, когда израсходована небольшая часть субстрата) увеличивается по мере роста концентрации субстрата в реакционной смеси. При неизменности остальных условий (концентрации фермента [Е], концентрации кофакторов, температуры, значения рН) это увеличение начальной скорости ферментативной реакции, в зависимости от концентрации субстрата происходит до тех пор, пока не наступит состояние насыщения фермента субстратом. Скорость реакции, измеренная в условиях насыщения, уже не зависит от дальнейшего повышения концентрации субстрата. Она достигает максимального значения, называемого максимальной скоростью реакции, V_max, которая далее остается постоянной.

В ферментативной кинетике обычно используют значительный молярный избыток субстрата по сравнению с концентрацией фермента. Например, если фермент с молекулярной массой 100.000 взаимодействует с субстратом с молекулярной массой 100 и оба компонента присутствуют в реакционной смеси в концентрации 1 мг/мл, каждый, то на один моль фермента будет приходиться 1000 молей субстрата. В клетке наиболее реальными являются следующие численные значения концентраций фермента и субстрата: [E] = 0,1 мкг/мл = 10 ^{– 9 М, [}S] = 0,1 мг/мл = 10 ^{– 3 М, т.е. молярный избыток субстрата по отношению к ферменту составляет величину, равную 106}. Даже при уменьшении [S] в 100 раз, его концентрация все еще будет 10.000-кратно превышать концентрацию фермента.

Уравнение Михаэлиса-Ментен

Важнейшим фактором, определяющим скорость ферментативной реакции, является концентрация реагирующих веществ, концентрация субстратов. Как было указано выше, фермент взаимодействует с субстратом с образованием фермент-субстратного комплекса. Затем фермент-субстратный комплекс распадается с образованием продукта реакции, а катализатор остается в исходном состоянии. Ниже приведено уравнение, отражающее процесс ферментативного катализа с образованием продукта реакции:

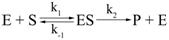
Как видно из этого уравнения, фермент Е взаимодействует с субстратом S с образованием фермент-субстратного комплекса ES. Этот процесс характеризуется константой скорости – k₁. Комплекс ES способен распадаться на исходные компоненты – Е и S с константой скорости k₋₁. Константа k₂ представляет собой константу скорости распада комплекса ES с образованием продукта реакции.

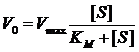
где К_M – константа Михаэлиса, которая равна концентрации субстрата (выраженной в молях/литр), при которой скорость реакции составляет половину максимальной скорости. Данное уравнение получило название уравнения Михаэлиса-Ментен. Графически зависимость между концентрацией субстрата и скоростью реакции отображает Рис. 6.1. Из этого рисунка видно, что при низких концентрациях субстрата реакция характеризуется первым порядком, а при его высоких концентрациях становится реакцией нулевого порядка, когда скорость реакции становится постоянной величиной.

Следует, однако, помнить, что уравнение Михаэлиса-Ментен справедливо только для начального времени реакции, когда присутствует избыток субстрата и образуется небольшое количество продукта. Именно поэтому уравнение Михаэлиса-Ментен носит несколько ограниченный характер, поскольку оно учитывает только первую часть процесса и не учитывает его вторую стадию – влияние продукта реакции и его взаимодействие с ферментом.

Графическое определение константы Михаэлиса (К_M)

Графически константа Михаэлиса может быть представлена, как это показано на Рис. 6.1. Однако в случае многих ферментов определение V_max и К_M непосредственно из графика зависимости V₀ от [S] (Рис. 6.1) оказывается затруднено. Для большего удобства уравнение Михаэлиса-Ментен было преобразовано Лайнуивером и Берком в координатах двойных обратных величин:

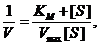
График уравнения Михаэлиса-Ментен в обрат­ных координатах называют графиком Лайнуивера-Берка (Рис. 6.2). Используя его, величину K_M можно определить либо по наклону прямой и длине отрезка, отсекае­мого на оси у, либо по длине отрезка, отсекаемого в области отрицательных значений на оси х. Поско­льку [S] измеряют в молях/литр, K_M имеет ту же размерность. Скорость V₀ мо­жет быть выражена в любых единицах, поскольку K_M не зависит от [E]. ГрафикЛайнуивера-Берка позволяет определять K_M по отно­сительно небольшому числу точек, поэтому он часто используется для расчета этого параметра.

Используя график Лайнуивера-Берка на прак­тике, при определении K_M, иногда сталкиваются с тем, что почти все точки оказываются в области низких кон­центраций субстрата. Это происходит в тех случаях, когда измерения проводят через равные интервалы [S]. Чтобы этого избежать, измерения следует прово­дить при таких значениях [S], которые соответ­ствуют равным интервалам на оси х в обратных ве­личинах.

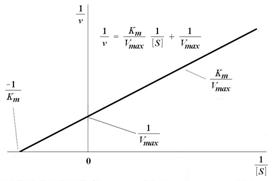
Рисунок 6.2 – График Лайнуивера-Берка в двойных обратных координатах (зависимость 1/V₀ от 1/[S]), используемый для графического определения K_M и V_max.

Определение K_M имеет большую практическую ценность. При концентрациях субстрата, в 100 раз превышающих K_M, фермент будет работать практически с макси­мальной скоростью, поэтому максимальная скорость, V_max, будет отражать количество присутствующе­го активного фермента. Это немаловажное обстояте­льство используют для оценки содержания фермен­та в препарате. Знание величины K_M позволяет определить, какое количество субстрата следует внести в реакционную смесь для определения V_max. Графики, построенные в обратных координатах, находят широкое примене­ние также при анализе характера действия ингибиторов в ферментативных реакциях.