Термодинамика необратимых процессов и ее применение к биологическим системам.

15.Классификация термодинамических систем. Первый закон термодинамики и его применение к биологическим системам. Второй закон термодинамики в биологии. Понятие термодинамического равновесия.
Термодинамика –наука, изучающая все виды энергии и процессы их взаимных превращений. Объект изучения – термодинамическая система.
Термодинамическая система – тело или группа тел, выбранных для изучения термодинамическими методами. Все тела, не входящие в термодинамическую систему, называют окружающей средой.
Поверхность раздела – реальная или воображаемая поверхность, отделяющая систему от окружающей среды.

Классификация термодинамических систем:

1. По числу фаз (гомогенные (1 фаза): H₂O; гетерогенные (несколько фаз): все живые организмы).

2. По возможности обмена с окружающей средой теплом и энергией (открытые (обмен массой и энергией): все живые организмы; закрытые (обмен энергией): запаянная ампула; изолированные (-): термос, сосуд Дюара.

Классификация ТД процессов:изотермический (температура – константа), изобарный (давление), изохорный (объем).

Первое начало термодинамки:Мерой передачи энергии в процессе теплообмена яявляется количество теплоты, а мерой передачи энергии в процессе работы является сама работа
Закон сохранения энергии для теплового процесса формулируется как первое начало термодинамики. Количество теплоты передаваемое системе идет на изменение внутренней энергии системы и совершение системой работы.

Применение первого начала термодинамики к живым организмам:В отличие от тепловых машин, живые организмы производят работу не за счет тепловой энергии, а посредством использования химической энергии пищевых продуктов, усвоенных ими. Поэтому положение, согласно которому изменение внутренней энергии равно ее обмену энергией с окружающей средой удобнее записать как
Дельта U= Wпищи- Q- A
Поскольку организм гомойотермных животных имеет постоянную температуру, поэтому внутренняя энергия такого организма приблизительно постоянна. Слепдовательно дельта У= 0.
Поэтому Wпищи= Q+ A.
Данная формула вполне соответствует приложению первого начала термодинамики к биологическим системам
Следует подчеркнуть ту особенность преобразования энергии пищи в энергию (работу) является тот момент, что нет промежуточного момента в виде образования свободной тепловой энергии.
Источники свободной энергии живого организма в виде совершаемых работ.

Второй закон термодинамики :постулирует существование особой функции состояния системы – энтропии (S).

Для обратимого изотермического процесса изменение энтропии равно количеству приведённого тепла, полученного системой.

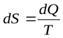, гдеdQ– количество тепла, полученного системой при температуреT.

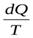- приведённое тепло.

Очевидно, что речь идёт о замкнутой системе, на её границе имеет место теплопередача.
Физический смысл энтропии– формула Больцмана: 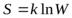, где
k– постоянная Больцмана
W– термодинамическая вероятность
Таким образом, энтропия – величина статистическая, она тем больше, чем больше термодинамическая вероятность данного макросостояния.
Энтропия – мера неупорядоченности системы.
В изолированных системах: энтропия изолированной системы возрастает, если протекающие в ней процессы необратимы (dS>0) и остаётся неизменной в обратимых процессах (dS=0). Необратимые процессы в изолированной системе приводят её в состояние термодинамического равновесия.

Термодинамическое равновесие:Фундаментальным для классической термодинамики является понятие термодинамического равновесия, которое тоже плохо поддаётся логическому определению и формулируется как обобщение экспериментальных фактов. Утверждается, что любая замкнутая термодинамическая система, для которой внешние условия остаются неизменными, с течением времени переходит в равновесное состояние, в котором прекращаются все макроскопические процессы. При этом в системе на микроскопическом уровне могут происходить самые разные процессы, например, химические реакции, которые могут протекать и в прямом, и в обратном направлении, однако в среднем эти процессы компенсируют друг друга, и макроскопические параметры системы остаются неизменными, флуктуируя относительно равновесного значения. Флуктуации изучаются в статистической физике.

Изменение энтропии в открытых системах. Термодинамические условия осуществления стационарного состояния. Связь межу величинами химического сродства и скоростями реакций. Термодинамическое сопряжение реакций и тепловые эффекты в биологических системах.

Применение второго закона к биологическим системам в его классической формулировке приводит, как кажется на первый взгляд, к парадоксальному выводу, что процессы жизнедеятельности идут с нарушением принципов термодинамики. В самом деле, усложнение и увеличение упорядоченности организмов в период их роста сопровождаются кажущимся уменьшением, а не увеличением энтропии, как должно было бы следовать из второго закона. Однако увеличение энтропии в необратимых самопроизвольных процессах происходит в изолированных системах, а биологические системы являются открытыми. Проблема поэтому заключается в том, чтобы, во-первых, понять, как связано изменение энтропии с параметрами процессов в открытой системе, а во-вторых, выяснить, можно ли предсказать общее направление необратимых процессов в открытой системе по изменению ее энтропии. Главная трудность в решении этой проблемы состоит в том, что мы должны учитывать изменение всех термодинамических величин во времени непосредственно в ходе процессов в открытой системе.

Итак, необходимо рассматривать организм не изолированно от внешней среды, а во взаимодействии с ней. Как известно, в изолированной системе самопроизвольно протекающие процессы приводят ее к состоянию так называемого термодинамического равновесия. При этом состоянии градиенты энергии выровнены, работоспособность системы равна нулю, а ее энтропия максимальна. Однако хорошо известно, что биологические системы, пока они функционируют, никогда не достигают такого состояния. Они всегда обладают работоспособностью, а их энтропия не максимальна. Это связано с тем, что биосистемы являются не изолированными, а открытыми системами. Они постоянно обмениваются энергией с внешней средой. При этом свободная энергия поступает в организм в виде пищевых продуктов, различных излучений и т.д, а выделяется чаще всего в деградированной тепловой форме или в виде низкоэнергетических соединений. Поскольку приток свободной энергии способствует уменьшению энтропии системы (увеличиваются градиенты энергии, уменьшается количество деградированной формы энергии), то нередко говорят, что организм питается отрицательной энтропией и выделяет положительную энтропию. Исходя из сказанного, для рассмотрения приложимости второго принципа термодинамики к биосистемам следует брать не организм как таковой, а организм вместе с участком среды, обеспечивающим его нормальное функционирование в течение определенного времени. Такая система получила название условно изолированной системы. В ней второй принцип термодинамики полностью приложим. В отдельных участках этой системы энтропия, казалось бы вопреки второму принципу термодинамики, может даже уменьшаться (например, в зеленом листе при фотосинтезе). Однако это уменьшение происходит за счет возрастания энтропии в другой части такой системы (например, в источнике света, от которого световая энергия поступает в лист). В результате общая энтропия такой системы в соответствии со вторым принципом термодинамики не уменьшается, а имеет тенденцию к увеличению. Таким образом, можно констатировать, что, так же как и к неживым объектам, второй принцип термодинамики приложим и к биосистемам. Протекание процессов в них идет в соответствии с этим принципом и энтропии здесь принадлежит важная роль.
Таким образом, постулат И.П. Пригожина состоит в том, что общее изменение энтропии dS открытой системы может происходить независимо либо за счет процессов обмена с внешней средой (d_eS), либо вследствие внутренних необратимых процессов (d_iS): dS=d_eS+d_iS.
Во всех реальных случаях d_iS>0, и только если внутренние процессы идут обратимо и равновесно, то d_iS=0. Для изолированных систем d_eS= 0, и это классическая формулировка второго закона: dS = d_iS =0. В клеточном метаболизме всегда можно выделить такие две группы процессов. Например, поступление извне глюкозы, выделение наружу продуктов ее окисления (d_eS) и окисление глюкозы в процессах дыхания (d_iS). В фотосинтезе приток свободной энергии света приводит к уменьшению энтропии клетки d_eS<0, а процессы дыхания, диссимиляции в клетке увеличивают ее энтропию d_iS>0. В зависимости от соотношения скоростей изменения d_eS и d_iS общая энтропия dS открытой системы может либо увеличиваться, либо уменьшаться со временем. Если единственной причиной необратимости и увеличения энтропии системы являются ее внутренние процессы, то они ведут к уменьшению ее термодинамического потенциала. В этом случае

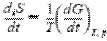
где G - полный термодинамический потенциал (или энергия Гиббса G = U + PV - TS).

Энергетическую характеристику открытой биологической системы в соответствии со вторым принципом термодинамики можно дать на основе баланса (обмена) энтропии. Это впервые сделал бельгийский ученый, лауреат Нобелевской премии И. Пригожин. Если обозначить dS /dt - скорость изменения энтропии открытой системы, d_iS/dt - скорость образования энтропии в системе за счет внутренних необратимых процессов, d_eS/dt – скорость обмена энтропией с внешней средой, то уравнение Пригожина имеет вид
dS/dt = dS_i/dt + dS_e/dt

причем член dS_i/dt по определению, всегда положителен, а член d_eS/dt может быть как положительным, так и отрицательным. Таким образом, это изящное уравнение в лаконичной и обобщенной форме выражает суть энергетических процессов, происходящих в открытой биологической системе.
Стационарным называется такое состояние открытой систе­мы, при котором основные макроскопические параметры систе­мы остаются постоянными.
Термодинамическим критерием (условием) стационарного со­стояния является равенство между продукцией энтропии орга­низмом и потоком энтропии из него в окружающую среду:

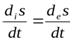
а полное изменение энтропии равно нулю:

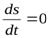(21)

Понятно, что термодинамическому равновесию свойственно отсутствие потока веществ между системой и средой, тогда как стационарное состояние открытой системы поддерживается бла­годаря обмену веществом и энергией со средой. Именно в ок­ружающей среде открытая система черпает свободную энер­гию, необходимую для поддержания стационарного состояния. Для сохранения термодинамического равновесия затрачивать свободную энергию не нужно,
В биологической системе термодинамическое равновесие ус­танавливается только при наступлении смерти. В обычных ус­ловиях жизни организм поддерживает стационарное состояние, которое характеризуется не отсутствием процессов, а таким ихтечением (обычно весьма активным и напряженным), при ко­тором они сбалансированы настолько, что основные параметры системы сохраняются неизменными, создавая внешнее впечат­ление «покоя».

Не существует какой-либо связи между величиной химического сродства и скоростью реакции. Реакции между веществами с большим химическим сродством могут протекать медленно, и наоборот, вещества с малым химическим сродством могут реагировать очень быстро. Так, согласно термодинамике, смесь газообразных водорода и кислорода при обычной температуре должна практически полностью превращаться в воду (для этой реакции DG^o = –450 кДж), однако в эксперименте образование воды практически не наблюдается. Химический потенциал алмаза в обычных условиях больше химического потенциала графита и, следовательно, алмаз должен самопроизвольно превращаться в графит, в действительности же такое превращение не происходит.
Такое кажущееся противоречие между теоретическими предсказаниями и практическими результатами обусловлено тем, что в термодинамике учитывается только начальное и конечное состояния системы, но не рассматривается механизм перехода и не фигурирует такой практически важный фактор как время. Реально всякое превращение связано с преодолением некоторого энергетического барьера – разрыв связей в молекулах реагирующих веществ, перестройка структуры кристаллической решетки и т.д. Если энергетический барьер высок, то теоретически возможная реакция протекает настолько медленно, что за практически ограниченный промежуток времени каких-либо изменений не наблюдается (реакция “не идет”).

Таким образом, кроме термодинамического подхода, громадное значение приобретает и другой аспект исследования химических реакций – изучение их с точки зрения скоростей

Следствием первого закона термодинамики является закон Гесса, утверждающий, что тепловой эффект реакциине зависит от пути реакции, а только от начального и конечного состояний.
17.Понятие обобщенных сил и потоков. Линейные соотношения и соотношения взаимности Онзагера. Стационарное состояние и условия минимума скорости прироста энтропии. Теорема Пригожина. Осуществление принципа Ле-Шателье в стационарных состояниях.
Обобщенные потоки и термодинамические силы могут быть связаны так называемыми соотношениями Онзагера. Эта связь ограничивается принципом Кюри, запрещающим взаимную связь явлений различной тензорной размерности.
Обобщенные потоки зависят от обобщенных сил, и наоборот - скорость химической реакции зависит от сродства, поток тепловой энергии - от разности температур.
Обычно обобщенные потоки определяются предыдущей историей образца.
Координаты обобщенных потоков и обобщенных термодинамических сил связаны между собой с помощью феноменологических коэффициентов.
Обобщённые потоки зависят от обобщённых сил (поскольку ими вызываются), и наоборот – скорость химической реакции зависит от сродства, поток тепловой энергии – от разности температур
Обобщённая сила — величина коэффициента при вариации обобщённой координаты в слагаемом выражения для виртуальной работы, относящимся к обобщённой координате.

Cоотношение Онзагера: Все термодинамические процессы характеризуются собственными значениями потока, скорости и движущей силы. Однако если в системе одновременно протекает несколько термодинамических процессов, процессы могут взаимодействовать друг с другом. В результате скорость каждого из них, иными словами, поток каждого термодинамического параметра будет зависеть не только от «своей» термодинамической силы, но и от движущих сил всех других процессов, происходящи в системе. Впервые принцип взаимодействия термодинамических процессов был выдвинут в 1931 году Л. Онзагером. Таким образом, уменьшение числа независимых феноменологических коэффициентов, необходимых для количественного описания неравновессных систем, достигается применением соотношения взаимности Онзагера. Согласно этому принципу многие взаимодействующие необратимые процесы могут быть описаны линейным дифференциальным уравнением с постоянными коэффициентами:

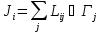, (11)

Где 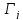– интенсивные термодинамические параметры (T, P, µ и т.д.), 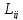-соответствующие коэффициенты, не зависящие от значения градиентов 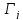, т.е. термодинамических сил 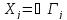. Соотношение взаимности Онзагера показывает, что если поток необратимого процессаi испытывает влияние термодинамической силы 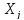необратимого процессаj через посредство коэффициента 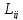, то и поток процессаj также испытывает влияние термодинамичесой силы 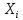через посредство того же самого коэффициента 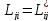. Данный принцип оказался очень плодотворным при рассмотрении многих необратимых процессов вблизи термодинамического равновесия ситемы, а сооотношение 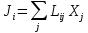в общем виде получили наименование линейных феноменологических уравнений взаимности Онзагера. При этом взаимодействующие термодинамические процессы называются сопряженными.Cоотношения взаимности Онзагера играют важную роль в термодинамике неравновесных процессов и, кроме того, находят непосредственное использование в анализе некоторых свойств мембранных, каталитических и биологических систем вблизи термодинамического равновесияю. Так, используя эти отношения и экспериментально определяя значения коэффициентов 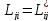, можно установить количественную взаимосвязь между одновременно протекающими в системе процессами даже в отсутствие детальной информации о механизме рассматриваемых процессов.

Теорема Пригожинаутверждает, что скорость продукции энтропии

внутри открытой системы в стационарном состоянии положительна и минимальна.

Она характеризует эволюцию открытой системы вблизи равновесия.

Следствие теоремы ПригожинаэтоПринцип Ле-Шателье. Если термодинамическую систему вывести из

состояния равновесия, в ней возникнут силы и потоки, стремящиеся вернуть

систему в исходное состояние равновесия.
18.Границы применимости линейной термодинамики в биологии. Критерий Удаленности сложных биологических процессов и их отдельных стадий от термодинамического равновесия. Нелинейная термодинамика. Общие критерии устойчивости стационарных состояний и перехода к ним вблизи и вдали от равновесия. Связь между кинетикой и термодинамикой.

Линейная термодинамика описывает стабильное, предсказуемое поведение систем, стремящих­ся к минимальному уровню активности, совместимому с питающими их потоками. Из того, что линейная нерав­новесная термодинамика так же, как и равновесная тер­модинамика, допускает описание с помощью потенциала, а именно производства энтропии, следует, что и при эво­люции к равновесию, и при эволюции к стационарному состоянию система «забывает» начальные условия. Ка­ковы бы ни были начальные условия, система рано или поздно перейдет в состояние, определяемое граничными условиями. В результате реакция такой системы на лю­бое изменение граничных условий становится предска­зуемой.

Второй закон термодинамики - опытный закон, установленный для замкнутых земных макросистем. В случае галактических систем определяющую роль в их поведении начинают играть дальнодействующие гравитационные силы, и такие системы уже нельзя считать замкнутыми. Этим определяется верхняя граница применимости второго закона: он неприменим к достаточно большим участкам Вселенной.
Между тем, некритическое перенесение закономерностей земного макроскопического опыта на Вселенную как целое приводило к антинаучным выводам о так называемой "тепловой смерти Вселенной", сделанным рядом физиков и философов в прошлом столетии. Распространяя действие второго закона на всю Вселенную, Р.Клаузиус пришел к выводу, что энтропия Вселенной стремится к максимуму. Следовательно, все виды движения во Вселенной должны самопроизвольно перейти в тепловое хаотическое движение, температура всех тел во Вселенной выравняется и наступит состояние "тепловой смерти" - в результате этого исчезнут причины, способствующие возникновению каких бы то ни было процессов.
Ошибочность подобных рассуждений заключалась в том, что Вселенной неправомерно приписывались свойства замкнутой системы. Кроме того, Вселенная непрерывно развивается, примерами чего могут служить ее расширение (данные астрофизики и космологии) и образование новых звездных систем. Для Вселенной само понятие термодинамического равновесия лишено смысла, поэтому для нее не существует состояния максимальной энтропии. Энтропия Вселенной в каждой ее области может возрастать неограниченно без приближения к состоянию максимальной энтропии, то есть к "тепловой смерти".
Таким образом, второй закон термодинамики применим только к изолированным термодинамическим системам.

Условием термодинамического равновесия всложных изолированных однородных системах является одинаковость температур, давлений и обобщенной силы Условия фазового равновесия дополняются условием равенства обобщенных сил в сосуществующих фазах. Следует иметь в виду, что выражение для химического потенциала сложной системы имеет вид.

В последние годы были развиты основы термодинамики сильно неравновесных систем, в которых связь между термодинамическими потоками и силами перестает быть линейной, а также не выполняется соотношение взаимности Онсагера.
Это направление, получившее название нелинейной термодинамики, приводит к возможности спонтанного возникновения упорядоченных структур в различных сильно неравновесных открытых системах, т.е. к процессу самоорганизации.
Общим во всех явлениях образования упорядоченных структур при необратимых процессах в сильно неравновесных открытых системах является совместное (кооперативное) движение больших групп молекул. Немецкий ученый Г.Хакен предложил для таких процессов самоорганизации общий термин «синергетика».
Физическая природа синергетики состоит в том, что в нелинейной области, вдали от равновесного состояния, система теряет устойчивость и малые флуктуации приводят к новому режиму – совокупному движению многих частиц.

В состоянии равновесия фундаментальную связь между термодинамикой (константа равновесия 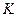) и кинетикой (константа скорости 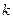) устанавливает закон Вант-Гоффа:

.

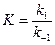 19. Связь энтропии и информации в биологических системах. Понятия количества и ценности информации. Условия запасания, хранения и переработки информации в макромолекулярных системах.

Согласно формуле Больцмана, энтропия определяется как логарифм числа микросостояний, возможных в данной макроскопической системе:

S = k_Б ln W,

где k_Б = 1,38 · 10^-16 эрг/град, или 3,31 · 10^{- 24} энтропийных единиц (1 э.е.= 1 кал/град = 4,1 Дж/К), или 1,38· 10^{- 23} Дж/К - постоянная Больцмана, W - число микросостояний (например, число способов, которыми можно разместить молекулы газа в сосуде).

Именно в этом смысле энтропия есть мера неупорядоченности и хаотизации системы. В реальных системах существуют устойчивые и неустойчивые степени свободы. Им соответствуют, например, твердые стенки сосуда и молекулы заключенного в нем газа.

Понятие энтропии связано именно с неустойчивыми степенями, по которым возможна хаотизация системы, а число возможных микросостояний намного больше единицы. В полностью устойчивых системах реализуется только одно-единственное решение, то есть число способов, которыми осуществляется это единственное макросостояние системы, равно единице (W = 1), а следовательно, энтропия равна нулю. В биологии использовать понятие "энтропия", а следовательно, и термодинамические представления можно только по отношению к конкретным метаболическим процессам, а не для описания в целом поведения и общебиологических свойств организмов. Связь энтропии и информации в теории информации была установлена для статистических степеней свободы. Допустим, что мы получили информацию о том, каким конкретно способом из всех возможных способов осуществлено данное макросостояние системы. Очевидно, количество информации, которое мы при этом получали, будет тем больше, чем больше была исходная неопределенность, или энтропия, системы.

Согласно теории информации, в этом случае количество информации о единственном реальном состоянии системы

I = log₂ W.

За единицу количества информации (бит) принимается информация, содержащаяся в достоверном сообщении, когда число исходных возможных состояний было равно W = 2:

I = log₂ W = 1 бит.

Например, сообщение о том, на какую сторону упала монета при бросании в воздух, содержит количество информации в 1 бит. Сопоставляя формулы можно найти связь между энтропией (в энтропийных единицах) и информацией (в битах)

S (э.е.) = 2,3 · 10^{- 24}·I бит.

Попытаемся формально оценить количество информации, содержащейся в теле человека, где имеется 1013 клеток. Считая, что все клетки уникальны и их нельзя менять местами без нарушения целостности организма, число способов которыми может быть составлена эта структура, составит W = 10¹³!, а количество информации, необходимое для ее построения,

I = log₂ (10¹³!) ~ 10¹³ log₂ 10¹³ ~ 4 · 10¹⁴ бит.

Такое количество информации необходимо было бы исходно получить, чтобы осуществить единственно правильное расположение клеток в организме. Этому эквивалентно весьма незначительное снижение энтропии системы на

dS = 2,3 · 10^{- 24} · 4 · 10¹⁴ ~ 10^{- 9} э.е. ~ 4 · 10^{- 9} Дж/К.

Если считать, что в организме осуществляется также уникальный характер расположения аминокислотных остатков в белках и нуклеиновых остатков в ДНК, то общее количество информации, содержащейся в теле человека, составит

I = 1,3 ·10²⁶ бит,

что эквивалентно небольшому понижению энтропии на dS = 300 э.е. = 1200 Дж/К. В процессах метаболизма это снижение энтропии легко компенсируется увеличением энтропии при окислении 900 молекул глюкозы.

Таким образом, биологические системы не обладают какой-либо повышенной информационной емкостью по сравнению с другими неживыми системами, состоящими из того же числа структурных элементов. Этот вывод на первый взгляд противоречит роли и значению информационных процессов в биологии.

Однако связь между I и S в справедлива лишь по отношению к информации о том, какое из всех W микросостояний реализовано в данный момент. Эта микроинформация, связанная с расположением всех атомов в системе, на самом деле не может быть запомнена и сохранена, поскольку любое из таких микросостояний быстро перейдет в другое из-за тепловых флуктуаций. А ценность биологической информации определяется не количеством, а прежде всего возможностью ее запоминания, хранения, переработки и дальнейшей передачи для использования в жизнедеятельности организма.

Основное условие восприятия и запоминания информации - способность рецепторной системы переходить вследствие полученной информации в одно из устойчивых состояний, заранее заданных в силу ее организации. Поэтому информационные процессы в организованных системах связаны только с определенными степенями свободы. Сам процесс запоминания информации должен сопровождаться некоторой потерей энергии в рецепторной системе для того, чтобы она могла в ней сохраниться достаточное время и не теряться вследствие тепловых флуктуаций. Именно здесь и осуществляется превращение микроинформации, которую система не могла запомнить, в макроинформацию, которую система запоминает, хранит и затем может передать другим акцепторным системам. Как говорят, энтропия есть мера множества незапоминаемых системой микросостояний, а макроинформация - мера множества их состояний, о пребывании в которых система должна помнить.

Информационная емкость в ДНК, например, определяется не только количеством определенных нуклеотидов, а общим числом микросостояний, включающих колебания всех атомов цепочки ДНК. Процесс запоминания информации в ДНК - это фиксация определенного расположения нуклеотидов, которое устойчиво вследствие образующихся химических связей в цепочке. Дальнейшая передача генетической информации осуществляется в результате биохимических процессов, в которых диссипация энергии и образование соответствующих химических устойчивых структур обеспечивают эффективность биологической переработки информации. В целом информационные процессы широко распространены в биологии. На молекулярном уровне они протекают не только при запоминании и переработке генетической информации, но и при взаимном узнавании макромолекул, обеспечивают специфичность и направленный характер ферментативных реакций, имеют важное значение при взаимодействии клеточных мембран и поверхностей. Физиологические рецепторные процессы, играющие самостоятельную информационную роль в жизнедеятельности организма, также основаны на взаимодействиях макромолекул. Во всех случаях макроинформация возникает исходно в виде конформационных изменений при диссипации части энергии по определенным степеням свободы во взаимодействующих макромолекулах. В результате макроинформация оказывается записанной в виде набора достаточно энергетически глубоких конформационных подсостояний, которые позволяют сохранять эту информацию в течение времени, необходимого для ее дальнейшей переработки. Биологический смысл этой макроинформации реализуется уже в соответствии с особенностями организации биологической системы и конкретными клеточными структурами, на которых разыгрываются дальнейшие процессы, приводящие в итоге к соответствующим физиолого-биохимическим эффектам.

Примером диссипативных структур являются ячейки Бенара. Опыт Бенара (1900 г.) состоит в следующем. Горизонтальный слой вязкой жидкости заключают между двумя параллельными поверхностями, причем нижнюю поверхность нагревают (например, на подогретую сковороду наливают слой минерального масла). Сначала жидкость находится в покое. Но за счет подогрева снизу создается разница температур. Из-за силы тяжести и выталкивающей силы Архимеда, тяжелые верхние слои и легкие нижние слои стремятся поменяться местами. До какого-то момента все внутренние движения гасятся силами вязкости. Но при достижении критической разности температур возникают конвекционные потоки, и слой жидкости вдруг скачком разделяется на шестиугольные ячейки, похожие на пчелиные соты.

Рис. 2.1 - Ячейки Бенара

Это явление, первоначально изучавшееся в рамках классической гидродинамики, в 70-х гг. ХХ в. было проанализировано с новой точки зрения и носит название неустойчивости Бенара.

Структура Бенара является примером самоорганизации. Тепловой поток выводит систему из равновесия. Пока система недалека от равновесия, движение внутри нее можно считать линейным. Производство энтропии в ней по теореме И. Пригожина будет минимальным. Теплота подается непрерывно, жидкость продолжает нагреваться, система удаляется от равновесия все дальше. Незначительные флуктуации, которые есть в любой системе и которые раньше затухали, начинают нарастать. Нарастание флуктуаций - характерный признак неустойчивости. Система удаляется от положения равновесия все дальше. Наконец, достигается некий порог (порог самоорганизации), когда в жидкости возникает ячеистая структура, новый порядок, устойчивый только в режиме постоянной подпитки. Ячейки Бенара, по существу, представляют собой гигантскую флуктуацию, стабилизируемую за счет обмена энергий с окружающей средой. Ячеистая конвекция служит хорошим примером того, что неравновесность может служить источником порядка.

Реакция Белоусова - Жаботинского представляет собой периодическую химическую реакцию, сопровождающуюся периодическим изменением цвета реакционной смеси. Эту пульсирующую реакцию называют химическим маятником. С ее теоретического обоснования в 70-х гг. ХХ в. началось развитие междисциплинарной науки - синергетики, т. е. науки о самоорганизации. Теоретическое объяснение реакции было получено бельгийскими учеными во главе с И. Пригожиным примерно через 20 лет после открытия, когда стала создаваться теория химической самоорганизации в рамках неравновесной термодинамики.

При исследовании периодической реакции Белоусова - Жаботинского экспериментально было обнаружено периодическое изменение концентраций ионов бромида и церия. Эту периодичность можно рассматривать как пространственно-временную диссипативную структуру, так как для ее возникновения требуется не только приток энергии, но и приток вещества. При этом, в процессе реакции часть вещества выпадает в осадок, т. е. происходит его диссипация. Это подтверждает опыт, который показывает, что продолжительность реакции при рассчитанных компонентах составляет около часа.

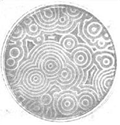Рис.2.2. Реакция Белоусова-Жаботинского

Колебания концентраций ионов бромида Br^- и церия Се³⁺ совершаются в противофазе: максимум одной концентрации совпадает с минимумом другой. Это позволяет для объяснения периодичности реакции применить аналогию с задачей "хищник - жертва" и считать, что компоненты ионов Br^- и Се³⁺ находятся в конкурирующих отношениях хищника и жертвы. Следовательно, реакция Белоусова - Жаботинского является примером самоорганизации.

Другим примером биологической самоорганизации является биение сердца, которое поддерживается целым комплексом периодических химических реакций.