Использование эффекта Джоуля-Томпсона

Вбольшинстве технических систем ожижения для получения низких температур используется дроссельный вентиль, или вентиль Джоуля — Томпсона.

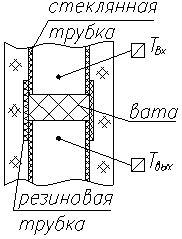
Применяя первый закон термодинамики для установившегося потока в дросселе при отсутствии теплообмена (изолированный дроссель) и нулевой передаче работы, для пренебрежимо малых изменений кинетической и потенциальной энергии находим, что h₁ = h₂. Хотя течение в дросселе необратимо и процесс не является изоэнтальпийным, входное и выходное состояния лежат на одной изоэнтальпе. Для ряда точек выходных условий можно построить зависимость от входных условий и получить линии постоянной энтальпии.

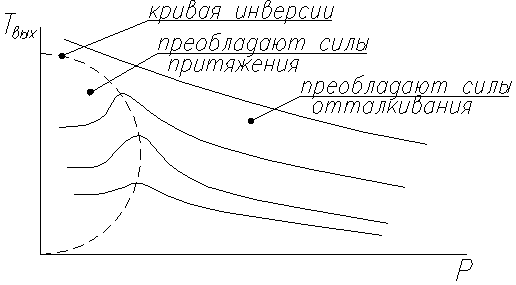
Для реального газа такая зависимость показана на рис. Отметим, что существует область, в которой дросселирование (уменьшение давления) приводит к увеличению температуры, тогда как в другой области — дросселирование приводит к уменьшению температуры. Очевидно, что в системах ожижения дроссель должен работать в области, где этот процесс приводит к общему уменьшению температуры. Кривая, разделяющая эти две области, называется кривой инверсии.

– подогрев

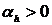– охлаждение

Тип газа	Тинв, К
He
H2
Ne
N2
O2
воздух

Рассмотрим проявление эффекта Джоуля-Томпсона на примере воздуха.

При начальных параметрах: , , 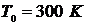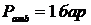; температура рабочего тела на выходе из дросселя составляет 35 К.

Эффект Джоуля-Томпсона используется во всех циклах ожижения газов.

Явление изменения температуры для изоэнтальпийного изменения давления характеризуется коэффициентом Джоуля — Томпсона μ_jT, определяемым как 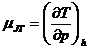, где производную следует рассматривать как изменение температуры при изменении давления при постоянной энтальпии.

Отметим, что коэффициент Джоуля - Томпсона есть угол наклона линий постоянной энтальпии. Коэффициент Джоуля - Томпсона на кривой инверсии равен нулю, так как эта кривая соединяет точки с нулевым наклоном изоэнтальп. Коэффициент Джоуля - Томпсона отрицателен для дросселирования с увеличением температуры; в процессе, происходящем с уменьшением температуры, коэффициент положителен.

Коэффициент Джоуля - Томпсона может быть выражен следующим образом

Для идеального газа μ_JT = 0. Идеальный газ не будет испытывать изменения температуры при расширении в дросселе. К удовлетворению инженеров, газы при достаточно низких температурах и высоких давлениях не являются идеальными.

Как было показано, идеальный газ всегда имеет нулевой коэффициент Джоуля - Томпсона, поэтому положительный или отрицательный коэффициент должен возникать как следствие отклонения поведения газа от идеального.

Энтальпия определяется как h = u+pv,

где и — внутренняя энергия вещества.

Делая эту подстановку, получаем .

Рассмотрим физический смысл членов этого уравнения.

Первый член уравнения характеризует отклонение от закона Джоуля, согласно которому внутренняя энергия идеального газа есть функция только температуры. Для реальных газов этот член всегда отрицателен, и показывает вклад в процесс уменьшения температуры (положительный μ_JT).

По мере того, как молекулы удаляются друг от друга с уменьшением давления при расширении, их микроскопическая потенциальная энергия возрастает. Подвод внешней работы и теплоты отсутствует, и поэтому это увеличение потенциальной энергии должно компенсироваться уменьшением ми­кроскопической кинетической энергии. Температура является мерой микроскопической кинетической энергии, а любое уменьшение кинетической энергии ведет к уменьшению температуры.

Второй член уравнения характеризует отклонение от закона Бойля, который утверждает, что произведение давления и объема для идеального газа есть функция только температуры. Второй член в уравнении может быть положительным, отрицательным или нулевым. Если, например, pv=f(T) = RT, то этот член всегда равен нулю. При низких давлениях и температурах вблизи состояния насыщенного пара газы более сжимаемы, чем это предписывается законом Бойля, так как силы притяжения способствуют конденсации газа. В этом случае второй член уравнения отрицателен и вносит вклад в уменьшение температуры, что справедливо для газов при комнатной температуре, за исключением водорода, гелия и неона.

При высоких давлениях молекулы плотно прижаты друг к другу и работают силы отталкивания, Следовательно, газ менее сжимаем в этом диапазоне, чем это предопределяет закон Бойля. Такое поведение приводит к положительному значению второго члена в уравнении, что означает повышение температуры в процессе расширения. Положительное, отрицательное или нулевое значение коэффициента Джоуля - Томпсона зависит от относительного значения обоих членов уравнения.

Одним из уравнений, описывающих поведение реальных газов, является уравнение состояния Ван-дер-Ваальса. Кривую инверсии составляют точки, на которых коэффициент Джоуля - Томпсона равен нулю. Максимальная температура инверсии для газа Ван-дер-Ваальса есть температура на кривой инверсии при р = 0 (или b/v = O), или T_imax = 2a/(bR).

Все газы можно разделить на две группы: газы, для которых максимальная температура инверсии больше комнатной температуры (это большинство газов) и газы, для которых максимальная температура ниже комнатной (неон, водород и гелий).

Различие в уровне максимальной температуры инверсии определяет применение в системах ожижения эффекта Джоуля - Томпсона для получения низких температур или таких методов, как расширение в детандере или предварительное охлаждение.