Основные классы неорганических соединений, номенклатура.

Лекция №3: Газовые законы. Основные газовые процессы.

Газовые законы

Под парциальным давлением газа Р_п понимают давление этого газа в предположении, что при температуре смеси в объёме, занимаемом смесью, находится только рассматриваемый газ. В соответствии с законом Дальтона, давление смеси идеальных газов равно сумме парциальных давлений этих газов: Р= .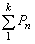

Для описания состояния идеального газа пользуются уравнением Менделеева-Клапейрона:

РV= 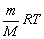, где: P – давление газа, Па; V – объём газа, м³; T – температура газа, К; m – масса газа, кг; M – мольная масса газа, кг/моль; R=8,31 Дж/(моль*К) – универсальная газовая постоянная.

Уравнением, объединяющим газовые законы Бойля-Мариотта и Гей-Люссака, является:

, где: индекс «0» означает начальное состояние системы, например, при нормальных условиях; индекс «1» означает некоторое конечное состояние системы. Нормальными условиями (н.у.) считают Р₀ =101,3кПа (нормальное атмосферное давление) и Т₀=298К (25°С). Однако во многих случаях приходится использовать в качестве нормальной температуры не 298К, а 273К (0°С). Это обусловлено тем, что многие справочные данные, необходимые для расчётов, получены не при 298К, а именно при 273К.

Плотность любого газа можно определить как:

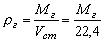, кг/м³. Где: М_г – мольная масса газа; V_ст=22,4 л/моль – объём, занимаемый 1 молем любого газа при н.у. (стандартный объём).

Плотность смеси газов определяется следующим образом:

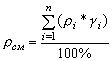, кг/м³. Где: r_i – плотность итого газового компонента смеси, кг/м³; g_i – объёмное содержание итого газового компонента смеси, %; n – количество газовых компонентов смеси.

Например, плотность атмосферного воздуха при н.у. составляет 1,29 кг/м³.

Плотность функционально зависит от температуры Т и давления Р:

Выведем функциональную зависимость плотности от температуры и давления. Для этого запишем объединённое уравнение в форме:

.

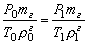
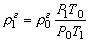Аналогично плотности смеси газов рассчитывается мольная масса смеси газов:

, г/моль. Где: М_i – мольная масса итого газового компонента смеси, г/моль; g_i – объёмное содержание итого газового компонента смеси, %; n – количество газовых компонентов смеси.

Например, мольная масса атмосферного воздуха при н.у. составляет около 29 г/моль.

Основные газовые процессы

Процессы, в которых участвует система, могут протекать при различных условиях. В связи с этим различают следующие основные варианты реализации указанных процессов.

1. Изохорный процесс. Объём системы остаётся постоянным (dV=0). Поэтому элементарная работа расширения системы dА_р=PdV=0, а вся теплота, сообщенная системе расходуется на изменение внутренней энергии, т.е. теплота приобретает свойства функции системы (не зависит от пути процесса): dQ_v=dU или Q_v=U₂-U₁.

2. Изобарный процесс. Давление Р=соnst. Таким образом dQ_p=d(U+PV), а работа расширения равна:

А_р=Р(V₂-V₁).

3. Изотермический процесс. Т=const. dQ_T=dA_p=PdVA_p=RT*ln(V₂/V₁)=

=RT*ln(P₁/P₂).

4. Адиабатический процесс. dQ=0. При адиабатическом процессе работа совершается системой за счёт убыли её внутренней энергии.

Более детально все эти процессы будут рассмотрены далее, в лекциях, посвящённых термодинамике. Здесь эти процессы указаны только для получения общих представлений. Следует также отметить, что наиболее общим случаем всех газовых процессов является политропный процесс (соотношение параметров выражено через величину n - показатель политропы).

Лекция №4: Строение атома.

Введение

Большую роль в установлении сложной природы атома и расшифровке его структуры сыграло открытие и изучение радиоактивности (явление испускания некоторыми элементами излучения, способного проникать через вещества, ионизировать воздух, вызывать засвечивание фотографических пластинок). Впервые в 1896г. радиоактивность обнаружена А. Беккерелем у соединений урана. Мария и Пьер Склодовские-Кюри обнаружили радиоактивность и у соединений тория, а в 1898 г. они открыли в составе урановых руд присутствие двух новых радиоактивных элементов – полония и радия. Опыты супругов Кюри показали, что атомы радия в процессе радиоактивного излучения распадаются, превращаясь в атомы других элементов, в частности, в атомы гелия. Впоследствии было установлено, что другим продуктом распада радия является инертный газ радон.

В 1903 г. Дж. Томсон предложил модель строения атома, согласно которой атом состоит из положительного ядра и электронов. Развивая эти представления, Э. Резерфорд в 1911г. предложил ядерную модель строения атома. Существенным шагом в развитии представлений о строении атома стала предложенная в 1913г. Н. Бором теория, объединившая, по сути, ядерную модель атома с квантовой теорией света. Основные положения своей теории Бор сформулировал в виде следующих постулатов: 1) электрон может вращаться вокруг ядра только по некоторым определенным круговым орбитам (стационарным орбитам); 2) Двигаясь по стационарной орбите, электрон не излучает электромагнитной энергии; 3) Излучение происходит при скачкообразном переходе электрона с одной стационарной орбиты на другую.

В 1900г. М. Планк предположил, что лучистая энергия испускается и поглощается телами не непрерывно, а дискретно. При этом, он определил энергию каждой такой порции как Е=h*n (уравнение Планка), где n – частота излучения; h=6,626*10^-34 Дж*с – постоянная Планка. Т.о. согласно определению Планка квант – это минимальная порция электромагнитного излучения с определенной частотой. В 1905г. А. Эйнштейн при изучении явления фотоэлектрического эффекта пришел к выводу, что электромагнитная энергия существует только в форме квантов, а излучение представляет собой поток неделимых материальных «частиц» - фотонов, энергия которых определяется уравнением Планка. Фотон не является ни частицей, ни волной – ему свойственна корпускулярно-волновая двойственность.

Атом и его строение

Атом любого элемента состоит из положительно заряженного ядра и отрицательно заряженных электронов, в целом же атом – система электронейтральная. Атомное ядро состоит из нуклонов: протонов (заряд +1, массовое число 1) и нейтронов (заряд 0, массовое число 1). Заряд ядра, равный порядковому номеру элемента в таблице Д.И. Менделеева, совпадает с числом протонов: массовое число ядра равно суммарному количеству протонов и нейтронов. У одного элемента возможно существование атомов с различным массовым числом ядер – изотопов, т.е. атомов с различным числом нейтронов и одинаковым числом протонов.

Согласно современным представлениям, электрон обладает одновременно свойствами волны и частицы, поэтому для описания его поведения нельзя пользоваться привычными характеристиками, такими как скорость и траектория движения. Вместо этого используют полную энергию электрона (сумма потенциальной и кинетической энергии) и вероятность обнаружения электрона в заданной области пространства.

Состояние электрона в атоме характеризуется волновой функцией, являющейся решением волнового уравнения Шредингера. Из математического анализа уравнения вытекает дискретность значений энергии электрона, момента количества орбитального движения и проекции этого момента на выделенное в пространстве направление. Дискретность выражается квантовыми числами: главным – n, орбитальным – l, магнитным - m_l . Четвёртое квантовое число - m_s, называют спиновым. Волновая функция при определённых значениях трёх квантовых чисел (n, l ,m_l) описывает состояние электрона, характеризующееся так называемой атомной орбиталью (АО).

Каждой АО соответствует область пространства определённого размера, формы и ориентации, равноценная понятию электронного облака. Электронное облако не имеет чётких границ, в связи с этим введено понятие граничная поверхность, т.е. поверхность с равной электронной плотностью, ограничивающая объём, который включает 90% заряда и массы электрона. Форма и размер граничной поверхности считается формой и размером электронного облака.

Главное квантовое число – n определяет энергию АО и номер энергетического уровня, на котором находится электрон (т.е. допустимые уровни энергии электрона) и может принимать значения от единицы до бесконечности.

Орбитальное квантовое число – определяет форму АО и энергетический подуровень (т.е. квантование вытянутости эллиптической орбиты) и может принимать значения от нуля до n- .

Магнитное квантовое число – m_l определяет пространственную ориентацию данной АО и отчасти её форму (т.е. ориентацию электронных облаков в пространстве) и может принимать значения от – …0…+ .

Спиновое квантовое число – m_s характеризует собственный момент импульса и связанный с ним магнитный момент (т.е. вращение электрона вокруг оси), и может принимать значения ± 1/2.

Число АО в пределах энергетического подуровня определяется числовым значением магнитного квантового числа (2 +1). Число АО в пределах всего энергетического уровня равно сумме АО всех его подуровней.

Строение атома фтора выражается электронной формулой 1s²2s²2p⁵ и электронно-графической формулой:

2s 2p

1s	¯­		¯­	¯­
	¯­

При заполнении АО действует принцип Паули (или запрет Паули), согласно которому в атоме не может быть двух электронов, у которых все четыре квантовых числа одинаковые. Основным следствием этого принципа является то, что на одной АО не может находиться более двух электронов. Состояние электронов в атоме должно отличаться значением хотя бы одного квантового числа. При переходах электронов с одной орбиты на другую атом поглощает или излучает энергию.

Принцип Паули определяет ёмкость (максимальное число электронов) энергетических уровней и подуровней, которая соответственно равна 2n² и 2(2 +1) т.е. удвоенному числу АО.

Заполнение энергетических подуровней подчиняется правилу Хунда, согласно которому устойчивому состоянию атома соответствует такое распределение электронов в пределах энергетического подуровня, при котором абсолютное значение суммарного спина атома максимально. Например, четыре валентных p – электрона атома кислорода размещаются в квантовых ячейках следующим образом:

2p

¯­

Закономерная последовательность заполнения энергетических уровней и подуровней в атомах с увеличением порядкового номера элемента выражается правилами Клечковкого, которые называют правилом суммы n+ . Согласно I-му правилу Клечковского, при росте заряда ядра атома последовательное заполнение электронных орбиталей происходит от орбиталей с меньшим значением суммы главного и орбитального квантовых чисел к орбиталям с большим значением этой суммы. При одинаковом значении этой суммы порядок заполнения электронами энергетических подуровней определяется II-ым правилом Клечковского: при одинаковых значениях суммы главного и орбитального квантовых чисел заполнение орбиталей происходит последовательно в направлении возрастания значения главного квантового числа. Т.о. первым заполняется подуровень с меньшим значением n в этой сумме:

1 s ® 2 s ® 2 p ® 3 s ® 3 p ® 4 s ® 3 d ® 4 p ® 5 s ®

4 d ® 5 p ® 6 s ® …

Правила Клечковского позволяют заранее предвидеть появление в периодической системе Д.И. Менделеева рядов из d - , а затем из f - элементов, которые находятся между s – и p – элементами больших периодов.

Принадлежность элемента к электронному семейству определяется характером заполнения энергетических подуровней: s- элементы – заполнение внешнего s - подуровня при наличии на предвнешним уровне двух или восьми электронов, например:

Li 1s² 2s²

р- элементы – заполнение внешнего p- подуровня, например:

F 1s² 2s² 2p⁵

d- элементы – заполнение предвнешнего d- подуровня, например:

V 1s²2s²2p⁶3s²3p⁶4s²3d³

f- элементы – заполнение f- подуровня второго снаружи уровня, например:

Nd 1s² 2s² 2p² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹⁰ 5p⁶ 6s² 4f⁴

Если на валентных энергетических уровнях имеются вакантные АО, то при возбуждении атома (получении ими порции энергии) становится возможным «разъединение» валентных электронов, то есть их переходы с тех подуровней, где все АО заняты полностью ( ¯­) или частично (¯) на другие валентные подуровни того же уровня, имеющие незаполненные АО. При этом с тех АО, которые в основном (соответствующем минимальной энергии атома) состоянии были заняты полностью, «уходит» по одному электрону последовательно, т.е. возможно несколько возбуждённых состояний. Возбуждение меняет валентное состояние атома (число его неспаренных электронов). Например, валентными электронами атома осмия в основном состоянии являются следующее: 5d⁶ 6s². Их распределение по квантовым ячейкам:

5d 6s

¯

¯

(атом осмия находится в 4–валентном состоянии).

При этом как на пятом, так и на шестом уровнях имеются вакантные АО. Получение атомом осмия двух последовательных порций энергии приводит к следующим возбуждённым состояниям - атом осмия находится: 1) в шести валентном состоянии; 2) в 8 – валентном состоянии.

I закон термодинамики

Термодинамику формируют три основных закона (или Начала). Первый закон термодинамики формулируется следующим образом: «Невозможно создать вечный двигатель первого рода (perpetuum mobile), т.е. такой, который производил бы работу без каких-либо затрат энергии». В раскрытии этого закона важную роль сыграли работы Гесса, Майера, Джоуля, Гельмгольца и др. Из этого закона следует принцип эквивалентности между теплотой и работой. Математическая запись данного закона выражается следующими уравнениями:

Q=DU+W

dQ=dU+dW

Теплота, полученная системой (dQ; Q), расходуется на работу (dW; W), совершаемую системой и увеличение ее внутренней энергии (dU; DU). Из этих трех энергетических величин только внутренняя энергия является функцией состояния системы и поэтому однозначно определяется параметрами системы (т.е. она является полным дифференциалом).

Теплота и работа представляют собой формы передачи энергии и поэтому являются функциями процессов. Они не являются полными дифференциалами.

Работа делится на совершаемую против внешних сил, т.е. работу расширения

dW_рас=PdV; W_рас=òPdV; W=-òVdP

и работу, не связанную с изменением объема, условно называемую ’’полезной’’ dW^/,

W^/= ådW^/

Последняя может совершаться только при изменении состава системы.

Теплота зависит от теплоемкости системы (с) и температуры

Q=ådQ=ònC(T)dT

Следует учитывать, что сама теплоемкость тоже зависит от температуры. Эта зависимость выражается уравнением (для случая, когда Т>Т₀=298К):

с(T)=a+bT+cT²+ c^/T^-2

Где: а, в, с, с^/ - коэффициенты, зависящие от природы и агрегатного состояния вещества, определены экспериментально и приведены в справочниках физико-химических величин. При использовании различных справочников результаты расчетов могут несколько отличаться.

В случае приближенных расчетов обычно достаточно использование выражения:

с(Т)=а+bТ

Для газообразных веществ различают теплоемкости при постоянном объеме (с_v) и постоянном давлении (с_р). Связь между этими величинами определяет уравнение Майера:

с_p-с_v=R Еслис_р,с_v – мольные, то R=const=8,31Дж/моль×К

с_p-с_v=R Еслис_р,с_v – массовые, то R=R_уд¹const

Например, для воздуха значение этой величины при н.у. равно ~280 Дж/кг×К

Для идеальных газов теплоемкости постоянны и без учета энергии колебательного движения молекул (что справедливо при сравнительно невысоких температурах) равны:

- для одноатомных молекул с_V=R×3/2;

- для двухатомных и линейных многоатомных молекул

с_V=R×5/2;

- для нелинейных трехатомных и многоатомных молекул

с_V=3×R.

Используя соотношение между теплоемкостями при постоянном давлении и постоянном объеме, выражают следующую величину показателя адиабаты:

g=с_P/с_V

значение которого для идеального газа зависит только от числа атомов в молекуле газа. Для теплоемкостей можно использовать и такие выражения как:

с_P=gR/(g-1)

с_v=R/(g-1)

для одноатомных газов g=5/3=1,67

для двухатомных газов g=7/5=1,40

для трехатомных газов g=9/7=1,30

Для жидких и твердых веществ теплоемкости с_р и с_V близки по величине:

с_р @с_V

Для систем, не совершающих полезной работы (W^/=0), первый закон термодинамики принимает вид:

dQ=dU+PdV

при V=const dQ_v=dU, Q_v=DU

при V=const dQ_P=dU+PdV=d(U+PV)

Величина Н=U+PV называется энтальпией (или теплосодержанием системы). Энтальпия, подобно внутренней энергии, является функцией состояния системы и определяется ее параметрами:

dQ_p=dH, Q_P=DH.

ЧАСТЬ 2.

III закон термодинамики. Теорема Нернста. Постулат Планка

Важное значение в раскрытии этого закона принадлежит работам Нернста и Ричардса. В частности, Нернст в 1906г. в своей классической работе «О вычислении химического равновесия из термических данных» высказал гипотезу, суть которой эквивалентна следующему утверждению:

при Т®0 S=0 и dS=0. Важнейшим следствием этой гипотезы является то, что энтропия правильно сформированного (бездефектного) идеального кристалла при 0К равна 0. Этот постулат впервые сформулировал Планк в 1912г. По сути, это и есть формулировка третьего начала (закона) термодинамики: lim_T®0S=0; S_T=òс(T)dT/T.

На основе этого закона разработаны современные методы вычислений изменения стандартной энергии Гиббса, а также констант равновесия при различных температурах.

Энергия Гельмгольца

Величина F=U-TS является функцией состояния системы и носит название изохорно-изотермического потенциала или энергии Гельмгольца (размерность энергии (Дж)). При Т,Р=const энергия Гельмгольца может служить признаком наличия равновесия или самопроизвольности процессов. При равновесии она постоянна и минимальна по величине. Самопроизвольно могут протекать только процессы, которые приводят к ее убыли.

Одноименного иона

Одноименными называют ионы, входящие в состав рассматриваемого труднорастворимого соединения. Если таковые в многокомпонентном растворе отсутствуют, то расчет растворимости ведут также по формуле (5), но с учетом ионной силы раствора. Вкладом труднорастворимого соединения в ионную силу пренебрегают, если его растворимость более, чем в 100 раз ниже концентрации других компонентов раствора. Ионную силу вычисляют как , а коэффициент активности как или , подставляя в последние вместо квадрата заряда иона модуль произведения зарядов ионов, образующихся при растворении труднорастворимой соли.

Следует подчеркнуть, что с ростом ионной силы g_± при не высоких концентрациях электролита понижается, а растворимость увеличивается.

Основные классы неорганических соединений, номенклатура.

Основными классами неорганических соединений являются оксиды, кислоты, соли и основания.

Оксиды представляют собой соединения элементов с кислородом. Оксиды подразделяют на солеобразующие и несолеобразующие. Солеобразующие оксиды делят на основные (образуют соли с кислотами), кислотные (образуют соли с основаниями) и амфотерные (образуют соли как с кислотами, так и с основаниями). Основным оксидам отвечают основания, кислотным – кислоты, а амфотерным – гидраты, которые проявляют как кислотные, так и амфотерные свойства. Кислотные оксиды представляют собой ангидриды кислот (SO₂ – серный ангидрид, N₂O₅ – азотный ангидрид).

Примеры: N₂O, NO - несолеобразующие оксиды; SO₃, SiO₂ - кислотные оксиды; СаО, МgО – основные оксиды и т.д.

В настоящее время общепринятой является международная номенклатура оксидов. Согласно международной номенклатуре в названии оксида указывается валентность элемента: СuO и Cu₂O – оксиды меди [II] и [III] соответственно. Существует также русская номенклатура, согласно которой окисью называется единственно возможный оксид элемента, в остальных случаях название дается в соответствии с числом атомов кислорода. Оксиды, в которых элемент проявляет низшую валентность, называются закисями.

Примеры: MgO – окись магния; NiO – одноокись никеля; Ni₂O₃ – полутораокись никеля; Сu₂О – полуокись меди.

Пероксиды (перекиси) металлов являются солями перекиси водорода Н₂О₂ и лишь формально относятся к оксидам. Приставка пер в названии соединений обычно указывает на принадлежность соединения к перекисным, но существуют исключения: соли кислот НMnO₄ (перманганаты) и НСlO₄ (перхлораты) перекисными не являются, а приставка пер в названии этих соединений указывает на максимальную насыщенность соединений кислородом.

Гидроксиды (основания) классифицируют по их силе (сильные – все щелочи кроме NH₄OH и слабые), а также по растворимости в воде (растворимые – щелочи и нерастворимые). Важнейшими щелочами являются КОН (едкое кали) и NaOH (едкий натр).

В состав кислот входит водород, способный замещаться металлом, а также кислотный остаток. Коэффициент х, отвечающий количеству атомов водорода, а, следовательно, равный валентности кислотного остатка, называют основностью кислоты. Кислоты классифицируют по их силе (H₂SO₄, HNO₃ – сильные кислоты; HCN – слабая кислота), на кислородсодержащие (H₂SO₄, HNO₃) и бескислородные (HCN, HI); а также по основности (х) -

HCN – одноосновная кислота, H₂SO₃ – двухосновная кислота, H₃РO₄ – трехосновная кислота. Важнейшим свойством кислот является их способность образовывать соли с основаниями. Названия кислот образуют от того элемента, которым образована кислота, при этом названия бескислородных кислот оканчивается словом водород (HCN –циановодород или синильная кислота). Названия кислородсодержащих кислот образуют от того элемента, которым образована кислота, с добавлением слова кислота (H₃AsO₄ – мышьяковая кислота, H₂CrO₄ – хромовая кислота). В случаях, когда один элемент образует несколько кислот различие между кислотами проявляют в окончаниях названий (на ная или овая оканчиваются названия тех кислот, в которых элемент проявляет наивысшую валентность; на истая или овистая оканчиваются названия тех кислот, в которых элемент проявляет валентность ниже максимальной).

Примеры:HNO₃ – азотная кислота, а HNO₂ - азотистая кислота; H₃AsO₄ – мышьяковая кислота, а H₃AsO₃ – мышьяковистая кислота.

Одному и тому же оксиду могут соответствовать несколько кислот, при этом наиболее богатая водой форма имеет в названии приставку орто, а наименее богатая – мета (ортофосфорная кислота H₃РO₄ – на одну молекулу ангидрида Р₂О₅ приходится три молекулы воды; метафосфорная кислота HРO₃ – на одну молекулу ангидрида Р₂О₅ приходится одна молекула воды). Следует также учитывать и то, что ряд кислот имеют исторически сложившиеся названия.

Соли являются продуктом замещения водорода в кислоте на металл или гидроксогрупп в основании на кислотный остаток. Нормальные (средние) соли получаются при полном замещении; кислые – при неполном замещении водорода кислоты на металл; основные – при неполном замещении гидроксогрупп основания на кислотный остаток. Кислая соль может быть образована только кислотой, основность которой 2 и более, а основная – металлом, заряд которого 2 и более.

Примеры:NaHS, KHCO₃ – кислые соли (гидросульфид натрия и гидрокарбонат натрия); MgOHCl, CaOHCl – основные соли (хлориды гидроксо магния и кальция); NaCl, CuS – нормальные соли (хлорид натрия и сульфид меди).

Название кислоты	Формула	Пример соли	Название соли
Серная	H2SO4	K2SO4	сульфат К
сернистая	H2SO3	Na2SO3	сульфит Na
соляная	HCl	Ca(Cl)2	хлорид Са
иодоводородная	HI	KI	иодид К
сероводородная	H2S	Na2S	cульфид Na
азотная	HNO3	KNO3	нитрат К
азотистая	HNO2	NaNO2	нитрит Na
ортофосфорная	H3РO4	K3РO4	ортофосфат К
хлорная	НСlO4	NaСlO4	перхлорат Na
хлорноватая	НClO3	NaСlO3	хлорат Na
хлористая	НClO2	NaСlO2	хлорит Na
хлорноватистая	НСlO	NaСlO4	гипохлорит Na
кремниевая	H2SiO3	CaSiO3	силикат Сa

Продолжение табл.

Название кислоты	Формула	Пример соли	Название соли
алюминиевая	H3AlO3	K3AlO3	алюминат К
ортоборная	H3BO3	K3BO3	ортоборат К
мышьяковая	HAsO4	KAsO4	арсенат К
мышьяковистая	HAsO3	KAsO3	арсениты К
двуфосфорная	H4P2O7	K4P2O7	дифосфат К
угольная	H2CO3	K2CO3	карбонат К
фосфористая	H3PO3	K3PO3	фосфит К
фтороводород	HF	KF	фторид К
хромовая	Н2СrO4	K2СrO4	хромат К
синильная	НCN	KCN	цианид К