Сущность и классификация хроматографических методов анализа. Тонкослойная хроматография.
Хроматография – это динамический метод разделения и опре- деления веществ, основанный на многократном распределении ком- понентов между двумя фазами – подвижной и неподвижной. Подвижной фазой может служить жидкость или газ, проте- кающие под давлением через слой неподвижной фазы.4 Неподвижная фаза (сорбент) представляет собой твёрдое по- ристое вещество с развитой поверхностью или плёнку жидкости, на- несённую на поверхность твёрдого инертного носителя. При хроматографировании вещество поступает в слой сорбен- та вместе с потоком подвижной фазы. При этом вещество сорбирует- ся, а затем при контакте со свежими порциями подвижной фазы – де- сорбируется. Перемещение подвижной фазы происходит непрерывно, поэтому непрерывно происходит сорбция и десорбция вещества. При этом часть вещества находится в неподвижной фазе в сорбированном состоянии, а часть – в подвижной фазе и перемещается вместе с ней. В результате скорость движения вещества оказывается меньше, чем скорость движения подвижной фазы. Чем сильнее сорбируется веще- ство, тем медленнее оно перемещается. Если хроматографируется смесь веществ, то скорость переме- щения каждого из них различна из-за разного сродства к сорбенту, в результате чего вещества разделяются: одни компоненты задержива- ются в начале пути, другие продвинутся дальше.Классификация хроматографических методов анализа:
В зависимости от агрегатного состояния фаз различают газовую хроматографию (подвижная фаза – газ или пар) и жидкостную хроматографию(подвижная фаза – жидкость).По механизму взаимодействия вещества с сорбентом различают следующие виды хроматографии: адсорбционная, распределительная, ионообменная, осадочная, окислительновосстановительная, комплексообразовательная и др.В зависимости от способа оформления процесса различают колоночную и плоскостную хроматографию. В колоночной хроматографии процесс разделения ведут в колонках, заполненных сорбентом. Плоскостная хроматография включает в себя две разновидности: хроматографию на бумаге и тонкослойную хроматографию на пластинках.В зависимости от способа хроматографирования различают следующие виды хроматографии: проявительная хроматография; вытеснительная хроматография; фронтальная хроматография.Чаще всего используется проявительный способ хроматографирования. Он заключается в том, что в непрерывный поток подвижной фазы (элюента) вводят смесь веществ, которыесорбируются лучше элюента. По мере движения элюента через колонку с сорбированными веществами они перемещаются вдоль слоя сорбента с различной скоростью и, наконец, выходят из неё отдельными зонами, разделёнными элюентом.По цели проведения хроматографического процесса различают: аналитическую хроматографию –
самостоятельный метод разделения, качественного и количественного анализа веществ; препаративную хроматографию для выделения чистых веществ из смеси.Тонкослойная хроматография — хроматографический метод, основанный на использовании тонкого слоя адсорбента в качестве неподвижной фазы. Он основан на том, что разделяемые вещества по-разному распределяются между сорбирующим слоем и протекающим через него элюентом, вследствие чего расстояние, на которое эти вещества смещаются по слою за одно и то же время, различается. Тонкослойная хроматография предоставляет большие возможности для анализа и разделения веществ, поскольку и сорбент, и элюент могут варьироваться в широких пределах. При этом коммерчески доступен ряд пластинок с различными сорбентами, что делает возможным быстрое и рутинное использование метода. Разновидностью тонкослойной хроматографии является более надёжная и воспроизводимая высокопроизводительная тонкослойная хроматография, при проведении которой используются специальные пластинки и сложное оборудование
59)Первое начало термодинамики. Теплота и работа как формы передачи энергии. Расчет энергии, теплоты, и работы в изотермических, изобарных, изохорных и адиабатических процессах. Зависимость теплового эффекта реакции от температуры. В каждом теле, в каждом веществе в скрытом виде заключена внутренняя энергия, которая складывается из кинетической энергии частей с-мы ( поступат, вращат, колебат движ-е), потенциальной энергии межмолекулярного вз-я, энергии хим связи, ядерная энергия. Т.к. в хим р-ях не происх ядерной перестройки, то изм-е внутр энергии с-мы есть изм-е кинетич, потенц и химич энергий составляющих компонентов ΔU = U2 - U1=ΔЕк+ ΔЕп+ ΔЕх. Абсолютную величину внутренней энергии определить невозможно. Поэтому можно судить только о суммарном изм-и внутр энергии в виде теплоты и работы. Однако можно определить ее изменение U при переходе из одного состояния в другое: ΔU = U2 - U1 , где U2 и U1- внутренняя энергия системы в конечном и начальном состояниях. Если ΔU > 0–внутренняя энергия системы возрастает, если ΔU < 0– внутренняя энергия системы убывает. U – термодинамическая функция состояния, так как ее количество не будет зависеть от пути и способа перехода системы, а будет определяться лишь разностью в этих состояниях. При переходе из одного состояния в другое система может обмениваться с окружающей средой веществом или энергией в форме теплоты и работы.
Теплота Q – рез-т изм-я внур Е, х-ся передачей хаотического поступат движения частиц данной системы или тела внешней среде. Такая передача наз-ся теплопередача. Энергия более нагретого тела в форме теплоты передается менее нагретому телу. При этом не происходит переноса вещества. Работа А – изм-е внутр энергии с-мы, связ с упорядоч поступлением движения от частей с-мы к внешней среде.
Теплота и работа – следствие обмена движения микрочастиц с-мы и внеш ср. Теплота и работа не являются св-ми системы. Их значение зависит от пути перехода с-мы из нач сост в конечное.
Теплоту и работу измеряют в джоулях (Дж), килоджоулях (кДж) и мегаджоулях (МДж). Положительной считается работа, совершаемая системой против внешних сил (А > 0) и теплота, подводимая к системе (Q > 0). Теплота и работа зависят от способа проведения процесса, т.е. они являются функциями пути. Количественное соотношение между изменением внутренней энергии, теплотой и работой устанавливает первый закон термодинамики – з-н сохранения энергии: Q = ΔU + А. изм-е внутр энергии закрытой с-мы определяется кол-вом выделенной теплоты и совершенной работы. Если к системе подводится теплота Q, то она расходуется на изменение внутренней энергии системы ΔU и на совершение системой работы А над окружающей средой. Теплоту и работу можно измерить, отсюда,ΔU = Q – А.
Первый закон термодинамики является формой выражения закона сохранения энергии. Согласно этому закону, энергия не может ни создаваться, ни исчезать, но может превращаться из одной формы в другую. Его справедливость доказана многовековым опытом человечества.
Изохорные процессы. Если система осуществляет переход из одного состояния в другое при постоянном объеме ( реакция протекает в автоклаве), то работа расширения системы А = рΔV = 0 и Qv = ΔU = U2 – U1, т.е. если реакция протекает при постоянном объеме, то выделение или поглощение теплоты Q связано с изменением внутренней энергии системы. Графически в p-v-диаграмме изохорный процесс изображается линией, параллельной оси давлений Линии изохорного процесса в диаграмме состояния называется изохорой.  Связь между параметрами в изохорном процессе подчиняется закону Шарля
Связь между параметрами в изохорном процессе подчиняется закону Шарля 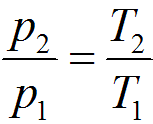
Изотермический процесс.Уравнение изотермического процесса: Т= const или pv = const.Графически изотермический процесс в р—v-диаграмме изображается в виде равнобокой гиперболы что вытекает из уравнения pv = const, и называется изотермой.
 Связь между параметрами изотермического процесса определяется законом Бойля — Мариотта:
Связь между параметрами изотермического процесса определяется законом Бойля — Мариотта: 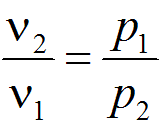 Так как Т1 = Т2, изменение внутренней энергии газа в изотермическом процессе равно нулю:
Так как Т1 = Т2, изменение внутренней энергии газа в изотермическом процессе равно нулю:
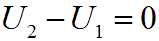 Работа газа в изотермич пр-се: A= νRTln(V2/V1) Q=A
Работа газа в изотермич пр-се: A= νRTln(V2/V1) Q=A
Изобарный процессУравнение изобарного процесса. р = const.
Графически изобарный процесс в р—v-диаграмме изображается прямой линией, параллельной оси объемов. Линия изобарного процесса называется изобарой.
 Связь между параметрами в изобарным процессе выражается законом Гей-Люссака:
Связь между параметрами в изобарным процессе выражается законом Гей-Люссака: 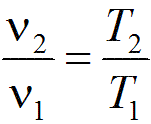
Изменение внутренней энергии газа рассчитывается по формуле: 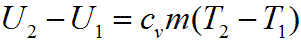
Изобарные процессы –при пост давлении протекают чаще всего. Работа A=PΔVВ этом случае тепловой эффект будет равен изменению внутр энергии системы+работа над внешн давл. Q = ΔU +pΔV. Если на систему не действуют ни какие другие силы, кроме постоянного давления, т.е. химический процесс осуществляется в изобарных условиях, и единственным видом работы является работа расширения, то первый закон термодинамики запишется: Q = ΔU + pΔV. Подставив ΔU = U2 ‑ U1, получим: Q= U2 ‑ U1 + pV2 ‑ pV1 = (U2 + pV2) ‑ (U1 + pV1).
Характеристическая функция U + pV = H называется энтальпией системы. Qp = H2 - H1, и Qp = ΔH. В случае изобарического процесса теплота, подведенная к системе, равна изменению энтальпии системы. Абсолютное значение энтальпии системы определить невозможно, но экспериментально можно определить Qp, т.е. изменение энтальпии ΔН, при переходе из одного состояния в другое. Н -это термодинамическая функция состояния. Если ΔН > 0 - энтальпия системы возрастает, если ΔН < 0-энтальпия системы уменьшается, т.е. теплота выделяется системой. Как и другие характеристические функции, энтальпия зависит от количества вещества, поэтому ее изменение ΔН, обычно относят к 1 моль и выражают в кДж/моль.
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Q=0, o=ΔU+A; ΔU=-A
Закон Гесса — математическое следствие первого начала термодинамики, которое формулируется следующим образом: Тепловой эффект химической реакции, проводимой в изобарно-изотермических или изохорно-изотермических условиях, зависит только от вида и состояния исходных веществ и продуктов реакции и не зависит от пути её протекания.
 Иными словами, количество теплоты, выделяющееся или поглощающееся при каком-либо процессе, всегда одно и то же, независимо от того, протекает ли данное химическое превращение в одну или в несколько стадий (при условии, что температура, давление и агрегатные состояния веществ одинаковы). Например, окисление глюкозы в организме осуществляется по очень сложному многостадийному механизму, однако суммарный тепловой эффект всех стадий данного процесса равен теплоте сгорания глюкозы.
Иными словами, количество теплоты, выделяющееся или поглощающееся при каком-либо процессе, всегда одно и то же, независимо от того, протекает ли данное химическое превращение в одну или в несколько стадий (при условии, что температура, давление и агрегатные состояния веществ одинаковы). Например, окисление глюкозы в организме осуществляется по очень сложному многостадийному механизму, однако суммарный тепловой эффект всех стадий данного процесса равен теплоте сгорания глюкозы.
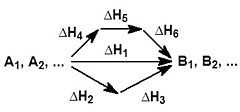
На рисунке приведено схематическое изображение некоторого обобщенного химического процесса превращения исходных веществ А1, А2… в продукты реакции В1, В2…, который может быть осуществлен различными путями в одну, две или три стадии, каждая из которых сопровождается тепловым эффектом ΔHi. Согласно закону Гесса, тепловые эффекты всех этих реакций связаны следующим соотношением:

Закон открыт русским химиком Г. И. Гессом в 1840 г.; он является частным случаем первого начала термодинамики применительно к химическим реакциям. Практическое значение закона Гесса состоит в том, что он позволяет рассчитывать тепловые эффекты самых разнообразных химических процессов; для этого обычно используют ряд следствий из него. Следствия из закона Гесса: 1Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции (закон Лавуазье — Лапласа).2.Тепловой эффект химической реакции равен разности сумм теплот образования (ΔHf) продуктов реакции и исходных веществ, умноженных на стехиометрическиекоэффициенты (ν):
 3. Тепловой эффект химической реакции равен разности сумм теплот сгорания (ΔHc) исходных веществ и продуктов реакции, умноженных на стехиометрические коэффициенты (ν):
3. Тепловой эффект химической реакции равен разности сумм теплот сгорания (ΔHc) исходных веществ и продуктов реакции, умноженных на стехиометрические коэффициенты (ν):
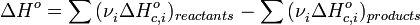
Таким образом, пользуясь табличными значениями теплот образования или сгорания веществ, можно рассчитать теплоту реакции, не прибегая к эксперименту. Табличные величины теплот образования и сгорания веществ обычно относятся к т. н. стандартным условиям. Для расчёта теплоты процесса, протекающего при иных условиях, необходимо использовать и другие законы термохимии, например, закон Кирхгофа, описывающий зависимость теплового эффекта реакции от температуры  .
. 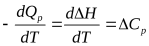 Если начальное и конечное состояния химической реакции (реакций) совпадают, то её (их) тепловой эффект равен нулю.
Если начальное и конечное состояния химической реакции (реакций) совпадают, то её (их) тепловой эффект равен нулю.
Кирхгофа уравнение равенство, выражающее температурную зависимость теплового эффекта химических реакций через разность теплоемкостей конечных продуктов и исходных веществ. В частности, для реакций, происходящих при постоянном объеме, К. У. связывает температурную зависимость изменения внутренней энергии ΔU при реакции с разностью изохорных теплоёмкостей Cv в форме  = Cv,2— Cv,1,, где Cv,1 и Cv,2 — суммы теплоёмкостей исходных веществ и продуктов реакции с учётом их стехиометрических коэффициентов в уравнении реакции. Интегрируя это уравнение, можно определить изменение внутренней энергии ΔUT при интересующей температуре Т, если известны ΔUT1 при какой-нибудь другой температуре T1 и теплоёмкости исходных веществ и продуктов реакции в рассматриваемом температурном интервале.
= Cv,2— Cv,1,, где Cv,1 и Cv,2 — суммы теплоёмкостей исходных веществ и продуктов реакции с учётом их стехиометрических коэффициентов в уравнении реакции. Интегрируя это уравнение, можно определить изменение внутренней энергии ΔUT при интересующей температуре Т, если известны ΔUT1 при какой-нибудь другой температуре T1 и теплоёмкости исходных веществ и продуктов реакции в рассматриваемом температурном интервале.
Адиабатический пр-с - термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. ΔQ=0, p=const1, t=const2 A=−ΔU
60)Молярные теплоемкости веществ как производные от внутренней энергии и энтальпии, расчет этих величин для идеального газа. Теплоемкость – это количество теплоты, которое необходимо сообщить системе для увеличения ее температуры на 1 ⁰(К) при отсутствии полезной работы и постоянстве соответствующих параметров.
Если в качестве системы мы берем индивидуальное вещество, то общая теплоемкость системы 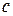 равняется теплоемкости 1 моль вещества (
равняется теплоемкости 1 моль вещества ( 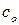 ) умноженное на число моль (
) умноженное на число моль (  ).
).
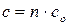 . (16 ) Теплоемкость может быть удельная и молярная. Удельная теплоемкость
. (16 ) Теплоемкость может быть удельная и молярная. Удельная теплоемкость  – это количество теплоты, необходимое для нагревания единицы массы вещества на 1 град (интенсивная величина).
– это количество теплоты, необходимое для нагревания единицы массы вещества на 1 град (интенсивная величина).
Молярная теплоемкость  – это количество теплоты, необходимое для нагревания одного моль вещества на 1 град.
– это количество теплоты, необходимое для нагревания одного моль вещества на 1 град.
Молярная теплоемкость в изохорном пр-се  – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1
– количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1 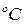 , если процесс происходит при
, если процесс происходит при  .
.
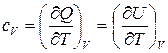 . (20)
. (20)
Молярная теплоемкость в изобарном пр-се 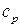 – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1
– количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1 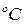 при
при 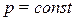 .
.
 . (21)
. (21)
Теплоемкость зависит не только от температуры, но и от объема системы, поскольку между частицами существуют силы взаимодействия, которые изменяются при изменении расстояния между ними, поэтому в уравнениях (20) и (21) используют частные производные.
Энтальпия идеального газа, как и его внутренняя энергия, является функцией только температуры:
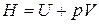 , а в соответствии с уравнением Менделеева–Клапейрона
, а в соответствии с уравнением Менделеева–Клапейрона 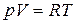 , тогда
, тогда
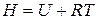 . (22)
. (22)
Поэтому для идеального газа в уравнениях (20), (21) частные производные можно заменить на полные дифференциалы:
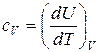 . (23)
. (23) 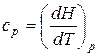 . (24)
. (24)
Из совместного решения уравнений (23) и (24) с учетом (22), получим уравнение взаимосвязи между 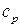 и
и  для идеального газа.
для идеального газа.
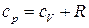 . (25)
. (25)
Разделив переменные в уравнениях (23) и (24), можно рассчитать изменение внутренней энергии и энтальпии при нагревании 1 моль идеального газа от температуры 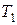 до
до 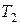
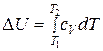 . (26)
. (26)  . (27)
. (27)
Если в указанном интервале температур теплоемкость можно считать постоянной, то в результате интегрирования получаем: 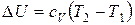 . (28)
. (28) 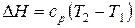 . (29)
. (29)
Установим взаимосвязь между средней и истинной теплоемкостью. Изменение энтропии с одной стороны выражается уравнением (27), с другой – 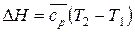 .
.
Приравняв правые части уравнений и выразив среднюю теплоемкость, имеем: 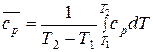 . (30)
. (30)
Аналогичное выражение можно получить для средней изохорной теплоемкости.
Теплоемкость большинства твердых, жидких и газообразных веществ повышается с ростом температуры. Зависимость теплоемкости твердых, жидких и газообразных веществ от температуры выражается эмпирическим уравнением вида:
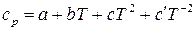 . (31)где а, b, c и
. (31)где а, b, c и  – эмпирические коэффициенты, вычисленные на основе экспериментальных данных о
– эмпирические коэффициенты, вычисленные на основе экспериментальных данных о 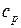 , причем коэффициент
, причем коэффициент 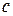 относится к органическим веществам, а
относится к органическим веществам, а 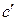 – к неорганическим. Значения коэффициентов для различных веществ приведены в справочнике и применимы только для указанного интервала температур.
– к неорганическим. Значения коэффициентов для различных веществ приведены в справочнике и применимы только для указанного интервала температур.
Теплоемкость идеального газа не зависит от температуры. Согласно молекулярно-кинетической теории теплоемкость, приходящаяся на одну степень свободы, равна  (степень свободы – число независимых видов движения на которые можно разложить сложное движение молекулы). Для одноатомной молекулы характерно поступательное движение, которое можно разложить на три составляющие в соответствии с тремя взаимно перпендикулярными направлениями по трем осям. Поэтому изохорная теплоемкость одноатомного идеального газа равна
(степень свободы – число независимых видов движения на которые можно разложить сложное движение молекулы). Для одноатомной молекулы характерно поступательное движение, которое можно разложить на три составляющие в соответствии с тремя взаимно перпендикулярными направлениями по трем осям. Поэтому изохорная теплоемкость одноатомного идеального газа равна
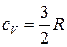 . (32)Тогда изобарная теплоемкость одноатомного идеального газа согласно (25) определится по уравнению
. (32)Тогда изобарная теплоемкость одноатомного идеального газа согласно (25) определится по уравнению 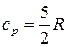 . (33)Двухатомные молекулы идеального газа помимо трех степеней свободы поступательного движения имеют и 2 степени свободы вращательного движения. Следовательно:
. (33)Двухатомные молекулы идеального газа помимо трех степеней свободы поступательного движения имеют и 2 степени свободы вращательного движения. Следовательно: 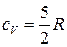 ,
, 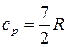 .
.
