Квантовые числа. Принцип Паули. Правило Хунда

Главное квантовое число, n – определяет энергию электрона и размер электронной орбитали, принимает дискретные значения:

n = 1, 2, 3, 4, 5, . . . . . , +∞.

Энергия электрона зависит от расстояния между электроном и ядром: чем электрон ближе, тем меньше энергия, которая определяется как E = –13,6 , эВ, где n– главное квантовое число.

Электроны в атоме могут находиться лишь в определенных квантовых состояниях, которые соответствуют конкретнымзначениям его энергии связи с ядром. Переход электрона из одного квантового состояния в другое связан со скачкообразным изменением энергии. Поэтому уровни энергии и связь энергии с главным квантовым числом n можно представить схемой (рис. 2.1).

Рис. 2.1. Схема уровней энергии и связь энергии

с главным квантовым числом

Таким образом, n характеризует принадлежность электрона тому или иному энергетическому уровню и соответственно размеры орбитали.

Орбитальное квантовое число, ℓ_n (ℓ)определяет форму орбитали (точнее симметрию), характеризует вращательную составляющую движения электрона. Различная форма электронных облаков обуславливается изменением энергии электрона в пределах одного энергетического уровня, то есть расщеплением ее на подуровни.

Электронное облако представляют по-разному, но чаще в виде граничной поверхности, внутри которой находится большая часть облака (~ 95 %).

Орбитальное квантовое число может изменяться в пределах: ℓ_n = 0, 1, . . . , (n – 1), где n – главное квантовое число. Кроме численных значений возможно буквенное обозначение орбитального квантового числа: s, p, d, f. Если связать воедино численное значение орбитального квантового числа с буквенным и пространственным изображением, то информация будет представлена в виде таблицы (табл. 2.2). Сферическая форма электронного облака характеризуется минимальным значением энергии (ℓ_n=0), и это облако обозначается как s-орбиталь и т.д.

Таблица 2.2

Значения орбитального квантового числа и

пространственное изображение орбиталей

Изображение орбитали
Значение ℓn
Буквенное обозначение	s	p	d	f

Очевидно, что при данном n орбитальное квантовое число принимает ряд значений, т.е. в пределах одного энергетического уровня возможно наличие различных форм орбиталей. Взаимосвязь орбитального и главного квантовых чисел представлена на

энергетической диаграмме (рис. 2.2).

Рис. 2.2. Энергетическая диаграмма уровней и подуровней в многоэлектронных атомах (взаимосвязь орбитального и главного квантовых чисел)

Для первого энергетического уровня возможно единственное значение ℓ_n,и оно равно нулю, т.е. форма орбитали сферическая. Для обозначения состояния электрона, для которого n=1 и ℓ_n =0, используется запись 1 s (табл. 2.3).

С переходом на второй энергетический уровень (n=2), ℓ_n принимает значения 0 и 1, следовательно, возможны состояния 2 s и 2 p; делаем вывод о возможности существования двух видов форм орбиталей и т. д.

Таблица 2.3

Значение и взаимосвязь орбитального и главного квантовых чисел, обозначение подуровней

№ уровня	Значение n	Значение ℓn	Обозначение подуровня
I	n=1		1 s
II	n=2		2 s 2 p
III	n=3		3 s 3 p 3 d
IV	n=4		4 s 4 p 4 d 4 f

Таким образом, различные значения ℓ_nв многоэлектронных атомах характеризуют энергетические подуровни в пределах каждого энергетического уровня, причем энергии s -, p -, d -, f- подуровней последовательно возрастают.

Количество подуровней на данном уровне соответствует номеру уровня. Каждый последующий уровень содержит все виды подуровней предыдущего плюс один.

Магнитное квантовое число, m_ℓ,характеризует пространственную ориентацию электронных облаков (определяет значение проекции орбитального момента количества движения на выделенное направление).

Магнитное квантовое число m_ℓ при заданном значении ℓ_n принимает набор значений от – ℓ_n, ... ,0, …, + ℓ_n. Т.е. конкретная форма электронного облака – орбитали, в пространстве ориентируется строго определенным образом.

При ℓ_n=0, форма орбитали сферическая (s-орбиталь) и в пространстве может быть ориентирована единственным образом, следовательно, магнитное квантовое число m_ℓ может принимать единственное значение равное 0.

Расположение гантелеобразного электронного облака (p-орбиталь) в пространстве возможно тремя способами, следовательно, магнитное квантовое число m_ℓможет принимать три значения равные -1; 0; +1.

Принимая за символ орбитали , связь между ℓ_n и m_ℓможно показать в виде табл. 2.4.

Таблица 2.4

Распределение орбиталей на подуровнях

ℓn	mℓ	Число орбиталей
0 (s)		1
1 (p)	-1 0 +1	3
2 (d)	-2 -1 0 +1 +2	5
3 (f)	-3 -2 -1 0 +1 +2 +3	7

Из таблицы видно, что s-подуровень имеет одну орбиталь, p-подуровень – три орбитали, d-подуровень – пять орбиталей, f-подуровень имеет семь орбиталей (рис. 2.3). Каждая из таких орбиталей характеризуется определенной комбинацией квантовых чисел n, ℓ_n и m_ℓ.

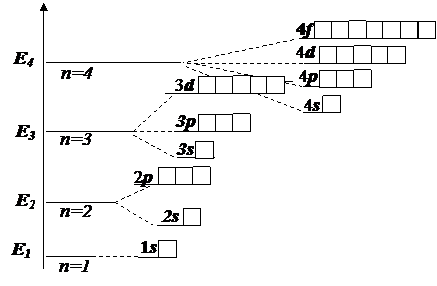Рис. 2.3. Энергетическая диаграмма уровней и подуровней в многоэлектронных атомах (взаимосвязь главного, орбитального и магнитного квантовых чисел)

Спиновое квантовое число, m_s. Электрон обладает собственным магнитным моментом, обусловленным его спином. Проекция в пространстве может иметь положительный или отрицательный знак. Если электрон обозначается ↑, значение m_s =+½. Если электрон обозначается ↓, то значение m_s = – ½.

Таким образом, совокупность положения электрона в атоме характеризуется определенными значениями квантовых чисел. Они определяют спин, энергию электрона, объем и форму пространства около ядра, в котором вероятно его пребывание.

Например, изображенный ниже электрон характеризуется следующим набором квантовых чисел: n = 5; ℓ_n =3; m_ℓ = -1; m_s = – ½.

Т.е. данный электрон находится на 5 энергетическом уровне, d-подуровне. электрон занимает вторую орбиталь и обозначается ↓.

При переходе атома из одного квантового состояния в другое происходит перестройка электронного облака, а значит, меняются значения квантовых чисел:

Состояние электронов в атоме отвечает принципу Паули: в атоме не может быть двух электронов, у которых были бы одинаковыми все четыре квантовых числа. Принцип Паули ограничивает число электронов, обладающих определенным значением главного квантового числа n: если n=1, то число электронов равно 2; если n=2, то число электронов 8 и т.д. Поэтому два электрона могут занимать одну орбиталь, если обладают противоположными спинами. Два электрона, находящиеся на одной орбитали, называются спаренными. Спаренныеэлектроны являются электронами с противоположными (антипараллельными) спинами.

При заполнении энергетических подуровней соблюдается правило Хунда: в данном подуровне электроны стремятся занять энергетические состояния таким образом, что бы суммарный спин был максимален.

Например, валентными электронами атома ₆С являются: 2s²2p². Определим, какое расположение электронов на p-подуровне отвечает устойчивому состоянию. Для этого согласно правилу Хунда рассчитаем абсолютное значение суммарного спина для двух вариантов расположения электронов представленных ниже.

а)

б)

Для случая а |1/2 – 1/2| = 0 и б |1/2 + 1/2| = 1.

Максимальнымабсолютным значением суммарного спина характеризуется состояние б, именно оно соответствует устойчивому состоянию атома ₆С.