Методические указания по разделам контрольной работы

Содержание

Введение................................................................................................................. 4

1 Общие рекомендации по оформлению контрольной работы........................... 5

2 Методические указания по разделам контрольной работы.............................. 6

2.1 Основные понятия и стехиометрические законы химии…………………6

2.2 Основные классы неорганических соединений…...……………………..11

2.3 Химическая кинетика и равновесие………………………………………17

2.4 Способы выражения состава растворов. Коллигативные свойства растворов………………...…………………………………………………26

2.5 Электролитическая диссоциация, ионное произведение воды, произведение растворимости……………………………………….…….32

2.6 Буферные растворы………….……………………………………………..40

2.7 Гидролиз солей……………………………………………………………..45

2.8 Жесткость воды…………………………………………………………….51

2.9 Коллоидно-дисперсные системы………………………………………….55

2.10 Окислительно-восстановительные реакции и электрохимические системы……………………..……………………………………………..60

3 Варианты заданий…………………………………………………………………...68

3.1 Варианты заданий при наличии в учебном плане одной контрольной работы……………………………………………………………………...68

3.2 Варианты заданий при наличии в учебном плане двух контрольных работ……………………………………………………………………….70

3.3 Условия контрольных заданий…………………………………………73

4 Программа дисциплины…………………………………………………………….92

5 Список рекомендуемой литературы……………………………….………………96

Заключение........................................................................................................... .97

Использованная литература................................................................................ .98

Введение

Настоящие методические указания составлены в соответствии c рабочей программой, полностью соответствующей ФГОС ВПО для бакалавров по направлению подготовки 270800 «Строительство». Они учитывают специфику данного направления подготовки и различный первоначальный уровень химических знаний студентов, а потому являются актуальными.

Целью данной методической разработки является повышение эффективности развития теоретических умений у студентов, что способствует формированию общекультурных и профессиональных компетенций, предусмотренных в ФГОС ВПО для указанного направления подготовки бакалавров.

Эта цель достигается существенной методической и дидактической поддержкой самостоятельной работы студентов при выполнении заданий контрольной работы.

Методический материал включает общие рекомендации по оформлению контрольной работы, краткие теоретические пояснения и примеры решения типовых задач по каждому разделу контрольной работы, список рекомендуемой литературы.

1 Общие рекомендации по оформлению

Контрольная работа выполняется в тонкой тетради в клеточку с отведенными полями.

На обложке указывается вид работы, номер варианта, факультет, курс, специальность, номер группы, фамилия, имя и отчество студента (полностью), номер зачетки (шифр).

Номер варианта определяется по двум последним цифрам зачетки (смотрите пояснения в таблице 1.1).

Таблица 1.1 – Определение номера варианта

Две последние цифры зачетки	Номер варианта

Если в учебном плане предусмотрена только одна контрольная работа, то номера контрольных заданий берутся из таблицы 3.1.

При наличии в учебном плане двух контрольных работ номера контрольных заданий определяются в соответствии с таблицей 3.2.

При оформлении работы указывается номер задания в соответствии с таблицей вариантов заданий (таблица 3.1 или таблица 3.2) и приводится его полный текст, затем следует решение со всеми необходимыми расчетами, уравнениями реакций и текстовыми пояснениями.

Работа сдается для регистрации в методический кабинет до начала экзаменационной сессии. Если контрольная работа содержит ошибки, их нужно исправить в соответствии с указаниями преподавателя, проверявшего работу, и выполнить работу над ошибками в той же тетради.

Студент, не предоставивший удовлетворительно выполненную контрольную работу, к экзамену не допускается.

Методические указания по разделам контрольной работы

Основные понятия и стехиометрические законы химии

Прежде чем приступать к решению задач этого раздела, необходимо четко уяснить понятия: относительная атомная и молекулярная массы, формульная масса, моль, постоянная Авогадро, молярная масса, молярный объем, эквивалент, число эквивалентности, количество вещества эквивалента, молярная масса эквивалента. Требуются также знания уравнения состояния идеального газа (уравнение Клапейрона-Менделеева), закона Авогадро и следствий из него, закона Дальтона для парциальных давлений газов, закона эквивалентов. Необходимо уметь выражать связь между массой, молярной массой и количеством вещества, а также связь между молярной массой эквивалента, количеством вещества эквивалента, массой и молярной массой вещества. Требуется научиться применять закон эквивалентов для нахождения масс и молярных масс веществ, участвующих или образующихся в реакции, уметь определять эквивалент и молярную массу эквивалента вещества в конкретной реакции.

Так как понятие эквивалента за последние десятилетия претерпело существенное изменение, для его усвоения следует пользоваться современными изданиями учебников.

Химическим эквивалентом называется реальная или условная частица вещества, которая может замещать, присоединять, высвобождать или быть каким-либо другим способом эквивалентна (равноценна) одному иону водорода в кислотно-основных и ионообменных реакциях, либо одному электрону в окислительно-восстановительных реакциях.

Реальные частицы – это атомы, ионы, молекулы и так далее, а условные частицы – это, например, 1/2 Н₂SO₄, 1/4 C, 1/3 Fe³⁺.

В общем случае эквивалент любого вещества X может быть записан в виде 1/z(X), где z – число эквивалентности, или эквивалентное число, которое всегда ³ 1. Оно показывает, сколько эквивалентов содержится в одной формульной единице вещества.

Для данного вещества z находится по конкретной реакции. В окислительно-восстановительных процессах z определяется числом электронов, принятых или отданных одной формульной единицей вещества. Рассмотрим окислительно-восстановительную реакцию

S + O₂ = SO₂

S⁰ - 4e^- = S⁺⁴

O₂ + 4e^- = 2O ^–2.

Формульная единица серы отдает 4 электрона, а одна формульная единица молекулярного кислорода принимает 4 электрона. Следовательно, z для серы и для кислорода равно четырем. Поэтому эквивалент серы в приведенной реакции - условная частица ¼ S, а эквивалент кислорода – ¼ О₂.

В ионообменных процессах величина z определяется стехиометрией реакции, причем для одного и того же вещества, в зависимости от реакции, эквивалентное число может иметь различное значение.

В качестве примера рассмотрим две реакции:

H₂SO₄ + NaOH = NaHSO₄ + H₂O;

H₂SO₄ + 2 NaOH = Na₂SO₄ + 2 H₂O.

Эквивалентом гидроксида натрия является реальная частица NaOH, для нее z = 1. В соответствии с уравнением первой реакции, один эквивалент NaOH взаимодействует с одной частицей H₂SO₄. Поэтому число эквивалентности для серной кислоты в этой реакции равно 1, а эквивалентом будет являться реальная частица H₂SO₄.

Во второй реакции два эквивалента гидроксида натрия реагируют с одной частицей серной кислоты, тогда один эквивалент NaOH взаимодействует с условной частицей 1/2 H₂SO₄, которая и будет являться эквивалентом серной кислоты во второй реакции. Таких частиц в формульной единице H₂SO₄ две, поэтому для серной кислоты в данной реакции z = 2.

Когда речь не идет о конкретной реакции, при определении z для сложных веществ можно воспользоваться следующими правилами:

- для оксидов z равно числу атомов элемента, умноженному на степень окисления элемента;

- для кислот z равно основности кислоты;

- для оснований z равно кислотности основания;

- для солей z равно числу катионов металла, умноженному на заряд катиона.

Количество вещества эквивалента обозначается n(1/z(X)). Единица измерения – моль. 1 Моль эквивалента вещества содержит 6,022×10²³ эквивалентов.

Молярная масса эквивалента М(1/z(X))– это масса 1 моль эквивалентавещества 1/z(X), измеряется в г/моль.

Связь между молярной массой эквивалента, количеством вещества эквивалента, массой и молярной массой вещества выражается соотношениями

(2.1.1)

Например, молярная масса эквивалента серной кислоты может быть вычислена как M(1/2H₂SO₄) = M(H₂SO₄):2 =98:2 = 49 (г/моль).

Закон эквивалентов гласит: «Эквивалентные количества всех веществ, участвующих в реакции, одинаковы».

n(1/z(X₁)) = n(1/z(X₂))(2.1.2)

Например, для реакции H₂SO₄ + 2NaOH = Na₂SO₄ + 2H₂O закон запишется в виде равенств

n(1/2 H₂SO₄) = n(NaOH) = n(1/2 Na₂SO₄) = n(H₂O)

Из закона эквивалентов следует, что массы реагирующих друг с другом веществ, а также массы продуктов реакции относятся друг к другу как молярные массы эквивалентов этих веществ.

В общем виде для двух компонентов реакции Х₁ и Х₂ справедлива формула

(2.1.3)

Если один из компонентов реакции, допустим Х₁, находится в газообразном состоянии, то для него справедливы соотношения:

;

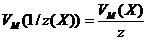где V(X) – объем газообразного вещества X;

V_M(1/z(X)) – объем, занимаемый одним моль эквивалента вещества Х;

V_M(X) – молярный объем газообразного вещества Х, равный при нормальных условиях 22,4 л/моль .

Тогда равенство (2.1.3) преобразуется к виду

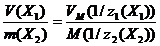(2.1.4)

Приведем другие формулы, использующиеся при решении задач этого раздела.

Молярная масса вещества М:

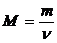, (2.1.5)

где m – масса вещества, г;

n - количество вещества, моль.

Единица измерениямолярной массы – г/моль.

Число Авогадро – число частиц, содержащихся в 1 моль.

N_A=6,02∙10²³ моль^-1.

Молярный объем V_M:

V_M = V:n, (2.1.6)

где V - объем газа;

n - количество вещества газа, моль.

При нормальных условиях молярный объем любого газа равен 22,4 л/моль (следствие из закона Авогадро).

Отношение масс равных объемов газов при одинаковых условиях равно отношению их молярных масс (следствие из закона Авогадро):

(2.1.7)

Величина называется относительной плотностью первого газа по второму.

Закон Дальтона для парциальных давлений не реагирующих друг с другом газов:

Р_общ.=Р₁+Р₂+…+Р_n , (2.1.8)

где Р_общ – общее давление смеси не реагирующих газов;

Р₁, Р₂, … Р_n – парциальные давления компонентов смеси.

Объединенный газовый закон:

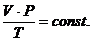(2.1.9)

Уравнение состояния идеального газа Клапейрона – Менделеева связывает между собой такие величины, как молярная масса газа М, его масса m, давление Р, объем V и температура Т:

, (2.1.10)

где R – универсальная газовая постоянная, равная 8,314 .

Пример 1

Определить молярную массу эквивалента Fe₂(SO₄)₃ в реакции

Fe₂(SO₄)₃ + 6 NaOH = 2 Fe(OH)₃ + 3 Na₂SO₄.

Решение

Одна формульная единица гидроксида натрия взаимодействует с одним ионом водорода, поэтому эквивалент щелочи есть реальная частица NaOH. По стехиометрии реакции на одну частицу NaOH (эквивалент) приходится 1/6частицы Fe₂(SO₄)₃, поэтому эквивалентом сульфата железа (III) в данной реакции будет условная частица 1/6 Fe₂(SO₄)₃.

Молярная масса эквивалента сульфата железа (III) в данной реакции может быть вычислена по формуле

M(1/6 Fe₂(SO₄)₃) = M(Fe₂(SO₄)₃) / 6 = 400 / 6 = 66,7 (г/моль).

Пример 2

Хлорид никеля массой 2,918 г взаимодействует с 1,8 г гидроксида натрия, молярная масса эквивалента которого равна 40 г/моль. Вычислить молярную массу эквивалента хлорида никеля.

Решение

В соответствии с законом эквивалентов

m(хлорида) / m(NaOH) = M(1/z хлорида) / M(1/1 NaOH).

Отсюда

M(1/z хлорида) = 2,918 × 40 / 1,8 = 64,8 (г/моль)

Пример 3

При сжигании 2,96 г металла было получено 4,91 г его оксида. Определить молярную массу эквивалента металла.

Решение

Найдем массу кислорода, израсходованного при горении металла. В соответствии с законом сохранения массы веществ

m(O₂) = m(оксида) – m(металла) = 4,91 – 2,96 = 1,95 (г).

При окислении металлов до оксидов газообразным кислородом происходит процесс: О₂⁰ + 4е^- = 2О^–2. Молекула кислорода принимает 4 электрона, следовательно, z = 4. На один электрон приходится 1/4 О₂, поэтому эквивалент молекулярного кислорода 1/4 O₂, а молярная масса эквивалента равна 8 г/моль.

По закону эквивалентов m(O₂) / m(Me) = M(1/4 O₂) / M(1/z Me);

Отсюда выразим M(1/z Me) и подставим численные значения величин:

M(1/z Me) = 2,96 × 8 / 1,95 = 12,1 (г/моль)

Пример 4

Некоторый газ, имеющий плотность по воздуху, равную 0,965, был собран в сосуд емкостью 2 л методом вытеснения воды и находится в нем при температуре 25^оС и давлении 99,8 кПа. Определите массу газа в сосуде, если давление паров воды составляет 3,17 кПа.

Решение

Так как газ был собран в сосуд методом вытеснения воды, то он содержит пары воды. В соответствии с законом Дальтона для смеси не взаимодействующих газов, общее давление газовой смеси складывается из парциальных давлений отдельных ее компонентов. Найдем давление неизвестного газа.

Р_газа=Р_смеси–Р_{пара воды}=99,8 кПа–3,17 кПа=96,63 кПа.

Зная относительную плотность газа по воздуху, рассчитаем его молярную массу в соответствии со следствием из закона Авогадро.

М_газа=D_возд.×М_возд=0,965×29 г/моль » 28 г/моль.

Выразим массу газа m из уравнения Клапейрона-Менделеева и подставим в полученное выражение все величины в единицах системы СИ.

;

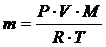
Итак, масса газа в сосуде равна 2,18 г.

Пример 1

Во сколько раз возрастет скорость реакций:

а) C + 2 H₂ = CH₄

б) 2 NO + Cl₂ = 2 NOCl

при увеличении давления в системе в три раза?

Решение

Увеличение давления в системе в три раза эквивалентно увеличению концентрации каждого из газообразных компонентов в три раза.

В соответствии с законом действующих масс запишем кинетические уравнения для каждой реакции.

а) Углерод представляет собой твердую фазу, а водород газовую. Скорость гетерогенной реакции не зависит от концентрации твердой фазы, поэтому она не входит в кинетическое уравнение. Скорость первой реакции описывается уравнением

Пусть начальная концентрация водорода равнялась х, тогда v₁ = kх². После увеличения давления в три раза концентрация водорода стала 3х, а скорость реакции v₂ = k(3х)² = 9kх². Далее найдем отношение скоростей:

v₁:v₂ = 9kx²:kx² = 9.

Итак, скорость реакции возрастет в 9 раз.

б) Кинетическое уравнение второй реакции, которая является гомогенной, запишется в виде . Пусть начальная концентрация NO равна х, а начальная концентрация Сl₂ равна у, тогда v₁ = kx²y; v₂ = k(3x)²3y = 27kx²y;

v₂:v₁ = 27.

Скорость реакции возрастет в 27 раз.

Пример 2

Температурный коэффициент скорости реакции g равен 2,8. На сколько градусов была повышена температура, если время протекания реакции сократилось в 124 раза?

Решение

В соответствии с правилом Вант-Гоффа v₁ = v₂× . Время реакции t есть величина, обратно пропорциональная скорости, тогда v₂/v₁ = t₁/t₂ = 124.

t₁/t₂ = = 124

Прологарифмируем последнее выражение:

lg( ) = lg124;

DТ/10×lgg= lg124;

DT = 10×lg124 / lg2,8 » 47⁰.

Температура была повышена на 47⁰.

Пример 3

При повышении температуры с 10⁰С до 40⁰С скорость реакции возросла в 8 раз. Чему равна величина энергии активации реакции?

Решение

Отношение скоростей реакции при различных температурах равно отношению констант скорости при тех же температурах и равно 8. В соответствии с уравнением Аррениуса

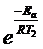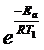k₂ / k₁ = A× / A = 8

Так как предэкспоненциальный множитель и энергия активации практически не зависят от температуры, то

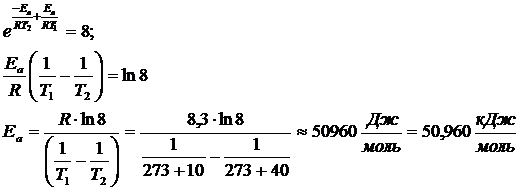
Пример 4

При температуре 973 К константа равновесия реакции

NiO+H₂ = Ni+H₂O_(г)

равна 0,32. Рассчитать равновесные концентрации веществ газовой смеси, если начальная концентрация водорода равна 3 моль/л.

Решение

Считаем, что начальная концентрация паров воды равнялась нулю. Выражение для константы равновесия данной гетерогенной реакции имеет следующий вид: .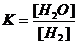

Пусть к моменту равновесия концентрация паров воды стала равна х моль/л. Тогда в соответствии со стехиометрией реакции, концентрация водорода уменьшилась на х моль/л и стала равной (3 – х) моль/л.

Подставим равновесные концентрации в выражение для константы равновесия и найдем х:

К = х / (3 – х); х / (3 – х)=0,32; х=0,73 моль/л.

Итак, равновесная концентрация паров воды равняется 0,73 моль/л, равновесная концентрация водорода равняется 3 – 0,73 = 2,27 моль/л.

Пример 5

Как повлияет на равновесие реакции 2SO₂+O₂ ⇄2SO₃; DH= -172,38 кДж:

1) увеличение концентрации SO₂, 2) повышение давления в системе,
3) охлаждение системы, 4) введение в систему катализатора?

Решение

В соответствии с принципом Ле Шателье, при увеличении концентрации SO₂ равновесие сместится в сторону процесса, приводящего к расходованию SO₂, то есть в сторону прямой реакции образования SO₃.

Реакция идет с изменением числа моль газообразных веществ, поэтому изменение давления приведет к смещению равновесия. При повышении давления равновесие сместится в сторону процесса, противодействующего данному изменению, то есть идущего с уменьшением числа моль газообразных веществ, а, следовательно, и с уменьшением давления. В соответствии с уравнением реакции, число моль газообразных исходных веществ равно трем, а число моль продуктов прямой реакции равно двум. Поэтому при повышении давления равновесие сместится в сторону прямой реакции образования SO₃.

Так как DН< 0, то прямая реакция идет с выделением тепла (экзотермическая реакция). Обратная реакция будет протекать с поглощением тепла (эндотермическая реакция). В соответствии с принципом Ле Шателье, охлаждение вызовет смещение равновесия в сторону реакции, идущей с выделением тепла, то есть в сторону прямой реакции.

Введение в систему катализатора не вызывает смещения химического равновесия.

Пример 6

Вычислить константу равновесия реакции FeO_(к)+H_2(г) ⇄Fe_(к)+H₂O_(г) при 25⁰С. В какую сторону смещено равновесие? Определить температуру установления равновесия, если все вещества находятся в стандартных состояниях, а зависимостью DH⁰ и DS⁰ от температуры можно пренебречь.

Решение

Константа равновесия связана с изменением стандартной энергии Гиббса реакции уравнением 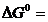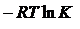, следовательно, .

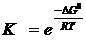Воспользовавшись справочными значениями стандартных энергий Гиббса образования веществ, найдем DG⁰_р-ции:

DG⁰_р-ции=DG⁰(H₂O_(г))+DG⁰(Fe_(к))-DG⁰(FeO_(к))-DG⁰(H_2(г))= -228,61 кДж/моль + + 0 – (-244,3 кДж/моль) – 0 = 15,59 кДж = 15,59 × 10³ Дж

К= 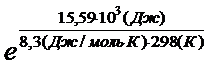=0,0018

Константа равновесия меньше единицы, следовательно, равновесие при 25⁰С (298 К) смещено в сторону обратной реакции.

В состоянии равновесия DG⁰= 0. Так как DG⁰= DН⁰ - TDS⁰, то равновесие установится при температуре T=DН⁰ / DS⁰.

Воспользовавшись справочными значениями стандартных энтальпий образования веществ и стандартных энтропий, вычислим DН⁰_р-ции и DS⁰_р-ции.

DН⁰_р-ции=DН⁰(Н₂О_(г))+DН⁰(Fe_(к))- DН⁰(FeO_(к)) -DН⁰(Н_2(г))= -241,82 кДж/моль+ + 0 – (- 263,7 кДж/моль) – 0 = 21,88 кДж.

DS⁰_р-ции=S⁰(Н₂О_(г)) + S⁰(Fe_(к)) - S⁰(FeO_(к)) - S⁰(Н_2(г)) =

=0,1887 кДж/моль× К + 0,02715 кДж/моль× К – 0,05879 кДж/моль× К –

- 0,13058 кДж/моль× К = 0,02648 кДж/К.

Найдем значение температуры, при которой установится равновесие:

Т = 21,88 кДж : 0,02648 кДж/К = 826 К.

Закон Рауля

, (2.4.11)

где Р₀ – давление насыщенного пара растворителя над чистым растворителем;

Р – давление насыщенного пара растворителя над раствором;

х – мольная доля растворенного вещества.

Следствия из закона Рауля

1) Повышение температуры кипения раствора

DТ_кип=_.К_Эб·b, (2.4.12)

где К_Эб – эбулиоскопическая постоянная растворителя;

b – моляльная концентрация.

2) Понижение температуры замерзания раствора

DТ_з.=К_к·b, (2.4.13)

где К_к – криоскопическая постоянная растворителя;

b – моляльная концентрация.

Пример 1

Рассчитать массу CuSO₄ и объем воды, необходимые для приготовления
130 мл 8% раствора этой соли. Рассчитать молярную, моляльную, нормальную концентрации и титр раствора. Плотность 8% раствора CuSO₄ равна
1,084 г/cм³ (г/мл).

Решение

,

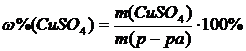m(р-ра)= r×V

m(CuSO₄)= =11,37 (г)

m(H₂O)=m(р-ра)-m(CuSO₄)= r×V - m(CuSO₄)=1,084×130-11,37=129,55(г).

Так как при комнатной температуре плотность воды близка к 1 г/см³, то масса воды, выраженная в граммах, численно равна ее объему в мл. Итак, объем воды равен 129,55 мл.

Рассчитаем молярную концентрацию раствора:

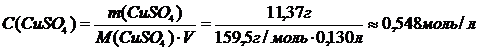
Нормальная концентрация:

.

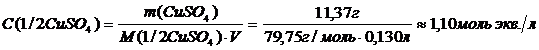Моляльная концентрация:

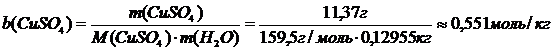
Титр раствора:

Пример 2

Какова молярная масса вещества, 24,731 г которого растворено в 1 л воды, если раствор замерзает при –0,5 ⁰С, а криоскопическая постоянная для воды равна 1,86 ?

Решение

DТ_з=К_к·b,

,

,

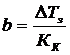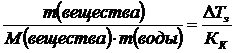Будем считать плотность воды равной 1 кг/л. Тогда масса воды равна 1кг.

Ответ: молярная масса вещества равна 92г/моль.

Пример 3

Рассчитайте массу глюкозы (С₆Н₁₂О₆), которая содержится в 100 мл раствора с осмотическим давлением 260 кПа при 5⁰С.

Решение

Из формулы (2.4.14) выразим и рассчитаем молярную концентрацию раствора.

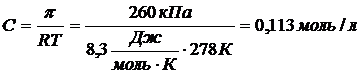
Рассчитаем массу глюкозы в 100 мл раствора:

m(С₆Н₁₂О₆)=C·M(С₆Н₁₂О₆)·V=0,113 моль/л·180 г/моль·0,1 л = 2,03г

Пример 4

Каково процентное содержание глюкозы (С₆Н₁₂О₆) в водном растворе, если понижение давления водяного пара над раствором составило 2,5% от давления пара над чистой водой.

Решение

В соответствии с условием задачи, понижение давления пара растворителя над раствором составит определенную долю от давления пара над чистым растворителем, то есть 0,025Р₀ или 25% от Р₀.

На основании закона Рауля

;

.

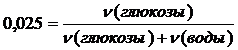Пусть для простоты имеется 100 г раствора глюкозы, тогда в нем содержится m граммов глюкозы и (100-m) граммов воды.

Решая данное уравнение относительно m, найдем массу глюкозы в 100 г раствора. Итак, масса глюкозы m=20,55 г.

Определим процентное содержание глюкозы в растворе:

.

Пример 5

Рассчитайте температуру кипения водного раствора сахарозы (С₁₂Н₂₂О₁₁), если его осмотическое давление при 27⁰С составляет 15,6 кПа. Эбуллиоскопическая постоянная воды 0,52 .

Решение

Из уравнения Вант-Гоффа для осмотического давления (формула 2.4.14) выразим и рассчитаем молярную концентрацию раствора сахарозы.

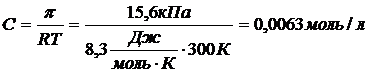
Масса сахарозы в 1 л раствора:

m(C₁₂H₂₂O₁₁)=M(C₁₂H₂₂O₁₁)·ν=342г/моль·0,0063моль=2,15г.

Плотность такого разбавленного раствора можно считать равной плотности воды, то есть приблизительно 1 г/мл. Тогда масса воды в 1 л раствора сахарозы составит

m(H₂O)=m(раствора) – m(C₁₂H₂₂O₁₁)=1000г – 2,15г = 997,85г

Рассчитаем повышение температуры кипения раствора сахарозы в соответствии с формулой (2.4.12).

DТ_кип=_.К_Эб·b=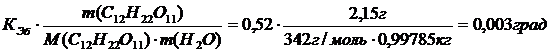

Температура кипения раствора сахарозы равна:

100⁰С+0,003⁰С =1 00,003⁰С.

Пример 1

Вычислите рН 0,01 М раствора HNO₃.

Решение

Азотная кислота является сильным электролитом, диссоциирует полностью. Концентрация катионов водорода будет равна концентрации кислоты. Активность ионов водорода является функцией концентрации ионов водорода.

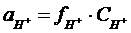
Коэффициенты активности ионов для растворов с различной ионной силой приведены в таблице 2.5.1.

Ионную силу раствора можно рассчитать по уравнению:

Из таблицы 2.5.1 для I=0,01 находим значение коэффициента активности f_H+=0.923.

Далее рассчитываем активность иона водорода и рН раствора:

а_н+ = 0,92·0,01 = 9,2·10^-3моль/л;

рН = -lg9,2·10^-3 = 2,04.

Примечание

В случае расчета рН раствора щелочи целесообразно сначала рассчитать гидроксильный показатель среды рОН, а затем найти водородный показатель среды по разности рН = 14 - рОН.

Пример 2

Вычислите рН 0,01 М раствора аммиака.

Решение

При расчете водородного показателя среды водных растворов слабых кислот и оснований следует учитывать обратимость процесса их электролитической диссоциации (α<1).

NH₃·H₂O ⇆ NH₄⁺ +OH^–

Концентрация ионов H⁺ в растворах слабых кислот и концентрация ионов ОН^– в растворах слабых оснований численно равны концентрации продиссоциировавших молекул электролита, а не исходной концентрации раствора, как в случае сильных кислот и оснований.

Концентрацию продиссоциировавших на ионы молекул электролита определяют, исходя из степени диссоциации:

С=αС_о,

где С_о - исходная концентрация молекул, моль/л.

Степень диссоциации рассчитывают на основании закона разбавления Оствальда, при этом константы диссоциации слабых электролитов берут из справочной литературы.

В случаях, когда расчет по упрощенному уравнению (2.5.2) дает результат α>0,1, вычисления повторяют по более точной формуле (2.5.1).

При вычислении водородного или гидроксильного показателя среды раствора слабой кислоты или слабого основания можно приближенно считать, что вследствие малых ионных сил растворов, активности ионов равны их молярным концентрациям.

Степень диссоциации NH₃·Н₂О в 0,01 М растворе равна:

=

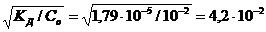
Находим концентрацию молекул NH₃·Н₂О, распавшихся на ионы, и равную ей концентрацию ионов ОН^-:

С=α·С_о = 4,2 10^-2 ·10^-2 = 4,2·10^-4 моль/л,

C_ОН^- = = 4,2·10^-4 моль/л.

Определяем рОН и рН 0,01 М раствора аммиака:

рОН = -lg С_ОН^- = -lg 4,2·10^-4 = 3,33

рН = 14 - 3,33 = 10,67.

Пример 3

Константа диссоциации HCN равна 6,2·10^–10. Вычислите массу цианид-анионов, содержащихся в 0,1 л раствора кислоты с концентрацией 0,1 моль/л.

Решение

Степень диссоциации HCN можно вычислить на основании закона разбавления Оствальда. Можно считать, что если отношение константы диссоциации слабого электролита к его концентрации больше 100, то можно пользоваться упрощенной формулой

.

.

Найдем массу цианид-анионов:

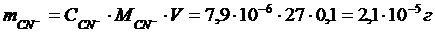
Пример 4

Какова ионная сила 0,01н. раствора Na₂SO₄ с учетом полной диссоциации соли?

Решение

Эквивалентом сульфата натрия является условная частица 1/2Na₂SO₄. Поэтому молярная концентрация раствора сульфата натрия будет в два раза меньше его нормальной концентрации, то есть равна 0,005 моль/л.

Так как одна частица Na₂SO₄ распадается на два катиона натрия и один сульфат-анион, то

C(Na⁺)=2C(Na₂SO₄)=0,01моль/л;

C(SO₄^2--)=C(Na₂SO₄)=0,005 моль/л.

Рассчитаем ионную силу раствора.

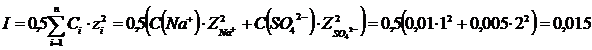
Ответ: ионная сила раствора равна 0,015.

Пример 5

Какова растворимость Ag₂CrO₄, выраженная в г/л, если величина произведения растворимости для этой соли составляет 1,3∙10^-12?

Решение

Ag₂CrO₄ ⇆ 2Ag⁺ + CrO₄^2–

ПР=[Ag⁺]² · [CrO₄^2—]

Пусть молярная концентрация Ag₂CrO₄ в насыщенном растворе равна x, тогда [CrO₄^2—]=x; [Ag⁺]=2x.

1,3∙10^--12 = (2x)²·x

1,3∙10^—12 = 4x³

C(Ag₂CrO₄)=x=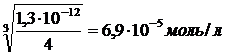

Для перевода этой величины в г/л, необходимо умножить ее на молярную массу Ag₂CrO₄:

6,9·10^--5моль/л ·332г/моль=0,023г/л

Ответ: растворимость Ag₂CrO₄ равна 0,023г/л.

Пример 6

Образуется ли осадок гидроксида железа (III), если к 1 л 0,006 М раствора хлорида железа (III) прибавить 0,125 л 0,0001 М раствора гидроксида калия? Произведение растворимости гидроксида железа (III) равно 3,8×10^-38. Степень электролитической диссоциации исходных веществ принять равной единице.

Решение

В насыщенном растворе гидроксида железа (III) устанавливается равновесие

Fe(OH)₃⇆Fe³⁺+3OH^-,

для которого произведение растворимости, в силу малой концентрации растворов, может быть выражено через равновесные молярные концентрации:

ПР=[Fe³⁺][OH^-]³.

Молярная концентрация катионов железа равна молярной концентрации хлорида железа (III), а концентрация ионов ОН^- равна концентрации гидроксида калия. Рассчитаем концентрации ионов, принимая во внимание, что после сливания растворов гидроксида железа (III) и гидроксида калия объем раствора стал 1 л + 0,125 л = 1,125 л.

,

[Fe³⁺][OH^-]³= 0,0053×(1,11×10^-5)³ = 7,2×10^-18.

Так как ПР<[Fe³⁺][OH^-]³, то в соответствии с (2.5.13) можно сделать вывод, что в заданных условия будет выпадать осадок гидроксида железа(III).

Буферные растворы

Буферными называют растворы, рН которых не изменяется при разбавлении или добавлении небольших количеств сильной кислоты или сильного основания.

Буферный раствор состоит из растворенных в воде слабой кислоты и ее соли, например, СН₃СООН и СН₃ССОNa, или из слабого основания и его соли, например, NH₄OH и NH₄Cl.

Из слабых многоосновных кислот и их кислых солей также можно приготовить буферные системы, например, Н₃РО₄ – NaH₂PO₄ или
NaH₂РО₄ – Na₂HPO₄.

Значения рН буферного раствора, состоящего из слабой кислоты и ее соли, рассчитывают по формуле (2.6.1):

рН= рК_НА - lg 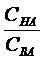, (2.6.1)

где С_НА и С_ВА – молярные концентрации кислоты и соли соответственно в буферном растворе, моль/л;

К_НА – константа диссоциации кислоты.

Из уравнения (2.6.1) следует, что значения рН буферных раств