Энергетика химических превращений
Химическое превращение есть качественный скачок, при котором исчезают одни вещества и образуются другие. Происходящая при этом перестройка электронных структур атомов, ионов и молекул сопровождается выделением или поглощением тепла, света, электричества и т.п. – превращением химической энергии в другой вид энергии.
Энергетические эффекты реакций изучает термохимия. Данные об энергетических эффектах реакций используются для расчетов тепловых балансов технологических процессов, для определения энергии межатомных и межмолекулярных связей, для выяснения строения и реакционной способности соединений, для установления направления химических процессов и т.д.
Химические реакции обычно протекают при постоянном давлении (например, в открытой колбе) или при постоянном объёме (например, в автоклаве). Процессы, протекающие при постоянном давлении, называют изобарными, а при постоянном объёме – изохорными.
Состояние системы описывается с помощью ряда переменных: давления, объёма, температуры, массы, энергии. На основе этих параметров могут быть выведены другие переменные, позволяющие характеризовать состояние системы и происходящие в ней изменения. Среди последних важное значение для химиков имеют внутренняя энергия U, энтальпия H, энтропия S, изобарный потенциал G и др.
4.1.1. Термохимия. Закон Гесса
Термохимия изучает тепловые эффекты химических процессов. Уравнения реакций, в которых учитываются их тепловые эффекты, называют термохимическими. В этих уравнениях выделение теплоты обозначают знаком (+), а поглощение – (–), например:
H2(г) + Сl2(г) = 2HСl(г) + 183,6 кДж или
1/2H2 (г)+ 1/2Сl2(г)= HCl (г) + 91,8 кДж∙моль-1
N2 (г)+ О2(г)= 2NО(г) – 180,4 кДж или
1/2N2 (г)+ О2(г)= NО(г) – 90,2 кДж∙моль-1
В термодинамике принята обратная система знаков, и выделение теплоты в результате химической реакции обозначают знаком ( - ), а поглощение теплоты- знаком (+).
Теплотой образования называют теплоту, которая поглощается или выделяется при образовании химического соединения количеством вещества 1 моль из простых веществ при заданных условиях; теплотой разложения – теплоту, которая поглощается или выделяется при разложении химического соединения количеством вещества 1 моль на простые вещества; теплотой сгорания - теплоту, которая выделяется при сгорании вещества 1 моль.
Согласно закону Лавуазье-Лапласа теплота разложения сложного вещества равна теплоте его образования из простых веществ, что является частным случаем закона сохранения энергии ΔU
В качестве стандартных условий в термодинамике принимается температура 2 0С. (298 К) и давление 1,013∙105 Па. Теплоты образования в этих условиях называют стандартными, для многих веществ они приводятся в таблицах справочной литературы.
Тепловые эффекты химических реакций связаны с изменением внутренней энергии системы при переходе от исходных веществ к продуктам реакции.
Внутренняя энергия (U) – это весь запас энергии системы, кроме потенциальной энергии её положения и кинетической энергии всей системы в целом. Таким образом, U слагается из поступательного и вращательного движений молекул, колебательного движения атомов и атомных групп в молекуле, движения электронов в атомах, ядерной энергии и т.д.
Если сиcтема поглощает из внешней среды теплоту Q, то внутренняя энергия U1 увеличивается на эту величину за вычетом той её части, которая расходуется на работу, совершаемую системой (А), т.е. U2 =U1 +Q-A или ΔU =Q-A , где ΔU= U2 -U1 .
Если в ходе процесса объём системы остается постоянным, т.е. работа расширения системы не совершается, то изменение внутренней энергии равно теплоте, поглощенной системой в условиях постоянного объёма: ΔU =Qv. Индексом V обозначают постоянство объёма. Изменение внутренней энергии ΔU, а следовательно, и Qv не зависит от пути процесса, что вытекает из закона сохранения энергии.
В химической практике чаще используют процессы, протекающие при постоянном давлении, когда объём системы может увеличиться на ΔV, в результате она совершит работу, равную рΔV. В этом случае процесс характеризуется энтальпией- величиной, которая определяется уравнением Н=U+pΔV. Изменение энтальпии Δ Н= ΔU+pΔV.
При стандартных условиях ΔН обозначают символом ΔН0298 .Для экзотермических реакций ΔН имеет отрицательные , а для эндотермических –положительные значения.
Если в ходе процесса при постоянном давлении системой совершается только работа расширения (А=рΔV), то ΔU= ΔН –pΔV или ΔU= ΔН – A, а так как ΔU=Q – A, то в этих условиях ΔН=Qp (индекс ”p” указывает постоянство давления). Так как ΔН не зависит от пути процесса, то этим свойством обладает и Qp.
Если реакция протекает в конденсированной системе, т.е. с участием только жидких и твердых веществ, то изменение объёма ΔV практически равно нулю. Тогда pΔV=0, и следовательно, ΔН=ΔV. В этом случае тепловые эффекты реакций при постоянном давлении и постоянном объёме практически равны между собой: Qv =Qр .
Поэтому при термохимических расчетах для конденсированных систем ограничивающие условия р= const или V= const опускаются.
Основным законом термохимии является закон Гесса (1840): тепловой эффект химических реакций, протекающих при постоянном объёме или при постоянном давлении, не зависит от числа промежуточных стадий и определяется только начальным и конечным состоянием системы.
Закон Гесса можно иллюстрировать схемой образования СО2: ΔН=ΔН1+ΔН2,
С ΔН СО2
 |
ΔН1 ΔН2
СО
т.е. тепловой эффект реакции равен сумме тепловых эффектов отдельных стадий. Из закона Гесса следует, что теплота образования вещества не зависит от способов его получения.
Следствие закона Гесса: стандартный тепловой эффект реакции равен сумме стандартных теплот образования продуктов реакции за вычетом суммы стандартных теплот образования исходных веществ:
ΔН0298(реакции)=∑ ΔН0298(прод.) -∑ΔН0298(исх.).
При термохимических расчетах энтальпии образования простых веществ (Н2, Сl2 и др.) в стандартном состоянии принимаются равными нулю. Поэтому тепловой эффект реакции синтеза соединений из простых веществ равен стандартной теплоте их образования. Например, для реакции
Н2(г)+ Вr2(г) → 2HВr(г) ΔН0298=2(-36,3)- (0+0)= -72,6 кДж,
т.е. тепловой эффект равен удвоенной стандартной теплоте образования НВr и реакция является экзотермической.
Закон Гесса позволяет также рассчитывать теплоты образования нестабильных соединений и тепловые эффекты реакций, которые нельзя осуществить экспериментально. Так, невозможно определить тепловой эффект реакции горения графита до оксида СО, т.к. при этом всегда образуется то или иное количество СО2. Однако тепловой эффект этой реакции может быть найден по экспериментально определенным теплотам сгорания графита до СО2 и сгорания CO до СО2:
С + О2 → СО2 ΔН =-393,5 кДж/моль
СО+ 1/2О2→ CО2 ΔН1 =-283,0 кДж/моль
С+ 1/2О2→ СО ΔН2 = ?
Согласно закону Гесса, ΔН= ΔН1 +ΔН2, откуда ΔН2 = ΔН - ΔН1 = - 393,5 – (-283,0) = -110,5 кДж/моль.
Энтропия
Большинство процессов представляет собой два одновременно происходящих явления: передачу энергии и изменение в упорядоченности расположения частиц друг относительно друга.
Частицам (молекулам, атомам, ионам) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное. Количественной мерой беспорядка является энтропия S. Изменение энтропии ΔS в изолированной системе, переходящей из состояния 1 в состояние 2, можно определить соотношением

где R- газовая постоянная.
Если, например, баллон с газом соединить с вакуумированным сосудом, то газ из баллона будет распределяться по всему объёму сосуда. При этом система из более упорядоченного состояния (с меньшим беспорядком) переходит в состояние менее упорядоченное (с большим беспорядком). Таким образом, при переходе системы из более упорядоченного состояния в менее упорядоченное состояние энтропия возрастает.
Переход же системы из менее упорядоченного состояния в более упорядоченное состояние связан с уменьшением энтропии, и самопроизвольное протекание подобного процесса менее вероятно. Так, ясно, что в рассматриваемом примере система самопроизвольно не может перейти из состояния 2 в состояние 1, т.е. невероятно, чтобы газ сам собой собрался в баллоне. В случае перехода системы из менее упорядоченного состояния в более упорядоченное ΔS системы - величина отрицательная, т.е. энтропия S системы уменьшается.
Энтропия возрастает при переходе жидкости в пар, при растворении кристаллического вещества и т.д. В процессах конденсации и кристаллизации вещества энтропия уменьшается. Энтропия вещества в газовом состоянии значительно больше, чем в жидком, а тем более, чем в твердом.
Энтропии веществ, как и их теплоты образования, принято относить к определенным условиям, обычно при температуре 25 0С (298 К) и давлении 1 атм. Энтропию при этих условиях обозначают S0298 и называют стандартной энтропией.
Значениями энтропии веществ пользуются для установления изменения энтропии системы в результате соответствующих процессов. Так, для химической реакции
аА+bB+…= dD+еЕ+…изменение энтропии системы будет
ΔS= (dSD + eSE+…)-( aSA + bSB+...) или ΔS= ∑Sпрод. - ∑Sисх.
Об изменении энтропии в химических реакциях можно судить по изменению объёма системы в ходе реакции. Например, в реакции ½ С (графит)+½ СО2(г)=СО(г) наблюдается увеличение объёма ΔV>0; следовательно, энтропия возрастает ΔS> 0 (ΔS0298=87,7 дж/моль∙град). В случае же реакции образования Н3N из водорода и азота 3/2 Н2 (г)+1/2 N2 (г)= H3N(г) наоборот, объём системы уменьшается ΔV<0; следовательно, энтропия уменьшается ΔS<0 (ΔS0298=99,1дж/моль∙град).
Если же реакция протекает между твердыми веществами, например,
Аl(к)+Sb(к)=АlSb(к), то изменения объёма системы и её энтропии практически не происходит (ΔS0298=4,03дж/моль∙град). То же самое относится и к процессам, в которых число молей газообразных веществ не изменяется, например, С (графит)+ О2 (г)= СО2 (г), ΔS=2,9дж/моль∙град.
4.1.3. Энергия Гиббса и направленность химических процессов
Возможность самопроизвольного протекания химического процесса определяется двумя факторами: стремлением системы к понижению внутренней энергии за счет экзотермической реакции (-∆H) и стремлением системы к увеличению неупорядоченности в расположении частиц за счет теплового движения, мерой которой является функция состояния, называемая энтропией S.
Если ∆H незначительно зависит от температуры, то энтропия с повышением температуры сильно возрастает. Влияние как энтальпийного так и энтропийного факторов учитывается в уравнении ∆G=∆H-T∆S. Функцию G называют энергией Гиббса, она является мерой устойчивости системы в условиях T=const и p=const.
Состояние системы при постоянном объеме описывается функцией, которую называют энергией Гельмгольца: ∆P=∆U-T∆S. Таким образом, ∆G отличается от ∆P так же, как ∆H от ∆U на величину, равную работе расширения p∆V.
Изменение энергии Гиббса ∆G определяет возможность или невозможность самопроизвольного протекания процесса. Если ∆G<0, т.е. по ходу реакции происходит уменьшение энергии Гиббса, то этот процесс термодинамически возможен. Если ∆G>0, т.е. процесс ведет к увеличению энергии Гиббса, то такая реакция термодинамически невозможна. Если ∆G=0, то реакционная система находится в состоянии равновесия.
При положительном значении ∆S и, следовательно, T∆S величина G будет отрицательной: а) при любых отрицательных значениях Н, т.е. все экзотермические процессы в этом случае возможны; б) при положительных значениях ∆Н, но при условии, что по абсолютному значению ∆Н<T∆S, т.е. эндотермические реакции возможны, когда энтропийный фактор преобладает над энтальпийным, что легче реализуется с ростом температуры.
При отрицательном значении ∆S в уравнении ∆G=∆H-T∆S величина T∆S становится положительной, поэтому в этом случае эндотермические реакции (+∆Н) самостоятельно протекать не могут, так как ∆G будет величиной также положительной. Из экзотермических реакций (-∆Н) при таком условии возможны только те, которые характеризуются большим отрицательным значением ∆Н, т.е. те эндотермические реакции, для которых сумма -∆Н+(-Т∆S) имеет отрицательное значение.
При очень низких температурах величина Т∆S минимальна, так как и энтропия в этих условиях изменяется незначительно, поэтому преимущественное влияние на направление процесса имеет энтальпийный фактор и обычно процессы идут в сторону экзотермических реакций. В конденсированных системах реакции протекают с незначительным изменением энтропии, поэтому знак ∆G определяется знаком ∆Н.
Таким образом, для определения возможности протекания процесса при данных условиях надо найти знак ∆G. С этой целью в справочных таблицах находят стандартные значения ∆Н и S для веществ, участвующих в реакции, по которым вычисляют ∆G на формулы ∆Go298=∆H o298-T∆S o298 [3].
Пример 1. Расчет теплового эффекта химической реакции по теплоте образования реагирующих веществ и продуктов реакции.
Определите количество теплоты, выделяющейся при гашении 100кг извести водой при 25оС, если известны стандартные теплоты образования веществ, участвующих в химической реакции:
∆H o298, CaO(к) = -635,1 кДж∙моль-1;
∆H o298, H2O(ж) = -285,84 кДж∙моль-1;
∆H o298, Ca(OН)2(к) = -986,2 кДж∙моль-1.
Решение. Реакция гашения извести: СаО(к)+Н2О(ж)=Са(ОН)2(к). Согласно первому следствию из закона Гесса тепловой эффект химической реакции равен разности между суммой теплот образования реагирующих веществ с учетом стехиометрических коэффициентов:

 =
=
=-986,2-(-635,1)-(-285,84) = 65,26 кДж∙моль-1
Таким образом, при гашении водой 1 моль извести выделяется 65,26кДж, при гашении 1кмоль извести – 65260 кДж. М(СаО) = 56г∙моль-1=56кг∙моль-1; m(СаО) = 100кг;

При гашении водой 100 кг извести выделяется 100/56∙65260=116536кДж.
Пример 2. Расчет теплоты образования.
Определить теплоту образования Са(ОН)2тв на основе реакций:
СаСО3→СаО+СО2+∆Н1; СаО+Н2О→Са(ОН)2тв+∆Н2.
Решение. Для определения суммарной теплоты образования ∆Н для этой реакции определяем ∆Н1 и ∆Н2, тогда ∆Н=∆Н1+∆Н2;
∆Н1=∆НСаО+∆Н(СО2)-∆НСаСО3 = +177,83 кДж∙моль-1;
∆Н2=∆НСа(ОН)2-∆НСаО-∆НН2О = -65,2 кДж∙моль-1;
∆Н= +177,83 – 65,2 = +113,61 кДж∙моль-1.
Пример 3. Рассчитайте тепловой эффект реакции горения сероводорода по следующим данным: Н2S(г) + 3/2O2=Н2О(ж) + SО2(г)
1)S(к) + Н2 = Н2S(г); ∆Н1= -20,17 кДж
2)Н2 + 1/2 O2 = H2O(ж); ∆Н2= -286,0 кДж
3)S(к) + О2 = SО2(г); ∆Н3= -297 кДж
Решение. Уравнение 1-3 есть термохимические уравнения образования соответственно 1 моль Н2S(г), Н2О(ж), SО2(г) из простых веществ в стандартных условиях: Т=298К и Р=101,325 кПа, а тепловые эффекты – стандартные энтальпии образования указанных соединений ∆H o298. Если сложить термохимические уравнения 2 и 3 и вычесть уравнение 1, получим искомое уравнение

Н2S(г) + 3/2 O2 = H2O(ж) + SO2(г) ∆Н=∆Н1+∆Н2-∆Н3
Подставить численное значение энтальпий образования Н2S(г) , Н2О(ж), SO2(г), получим значение теплового эффекта реакции ∆Н= -286 -297 –(-20,17) = = -562,8 кДж. Отрицательное значение энтальпии реакции горения сероводорода означает, что данная реакция экзотермическая.

Тепловой эффект можно включить в уравнение химической реакции.
Н2S(г) + 3/2О2 = Н2О(ж) + SO2(г) + 562,8 кДж. Эта запись также представляет собой термохимическое уравнение реакции.
Пример 4. Определение изменения энтропии в стандартных условиях. Определить изменение энтропии реакции Na2O+SiO2=Na2SiO3 при температуре 298К.
Решение. Находим по справочнику значения энтропии продукта и исходных веществ при Т=298К, S o298, Na2O(т)=42,09Дж∙моль-1∙к-1:
S o298, SiO2 (т) = 71,1Дж∙моль-1∙к-1;
S o298, Na2SiO3 (т)=113,8Дж∙моль-1∙к-1. Изменение энтропии в химической реакции равно разности между суммой энтропий продуктов реакции и суммой энтропий исходных веществ с учетом стехиометрических коэффициентов.
So298 х.р. = So298, Na2SiO3(т) – So298, SiO2 (т) - So298, Na2O(т) = 113,8-71,1-42,09=0,61 Дж∙моль-1∙к-1
Пример 5. Определение изменения энтропии при фазовых превращениях. Определить изменение энтропии 1г кристобалита при температуре плавления 1986К, если теплота обратного фазового превращения кристобалита равна 744,05 Дж∙r-1.
Решение. Изменение энтропии при переходе вещества из одного агрегатного состояния в другое равно:  , где ∆Н-теплота обратимого фазового превращения.
, где ∆Н-теплота обратимого фазового превращения.
S2-S1=∆S=  =
=  = 0,238Дж∙г-1∙град-1.
= 0,238Дж∙г-1∙град-1.
Пример 6.Вычислите  для химической реакции 2SO2(г)+О2(г)↔2SO3(г). В каком направлении может протекать эта реакция в стандартных условиях?
для химической реакции 2SO2(г)+О2(г)↔2SO3(г). В каком направлении может протекать эта реакция в стандартных условиях?
 , SO2(г) = -300,37 кДж∙моль-1;
, SO2(г) = -300,37 кДж∙моль-1;
 , SO3(г) = -370,37 кДж∙моль-1
, SO3(г) = -370,37 кДж∙моль-1
Решение. Изменение энергии Гиббса в химической реакции
 , поэтому в стандартных условиях данная реакция может протекать в сторону образования SO3.
, поэтому в стандартных условиях данная реакция может протекать в сторону образования SO3.
Химическая кинетика
Пример 1. При взаимодействии кристаллов хлорида фосфора (V) с парами воды образуется жидкий РОС13 и хлороводород. Реакция сопровождается выделением 111,4 кДж теплоты. Напишите термохимическое уравнение этой реакции.
Решение. Уравнения реакций, в которых около символов химических соединений указываются их агрегатные состояния или кристаллическая модификация, а также числовое значение тепловых эффектов, называют термохимическими. В термохимических уравнениях, если это специально не оговорено, указываются значения тепловых эффектов при постоянном давлении Qp, равные изменению энтальпии системы ∆Н. Значение ∆Н приводят обычно в правой части уравнения, отделяя его запятой или точкой с запятой. Приняты следующие сокращенные обозначения агрегатного состояния вещества: г — газообразное, ж — жидкое, к — кристаллическое. Эти символы опускаются, если агрегатное состояние веществ очевидно.
Если в результате реакции выделяется теплота, то ∆Н < 0. Считывая сказанное, составляем термохимическое уравнение данной в примере реакции:
РС15(к) + Н2О(г) = РОСl 3(ж) + 2НС1(г); ∆Нхр = -111,4 кДж
Таблица 3
Стандартные теплоты (энтальпии) образования  некоторых веществ
некоторых веществ
| Вещество | Состо- яние | ∆Н  , кДж/моль , кДж/моль | Вещество | Состо-яние | ∆Н  , кДж/моль , кДж/моль |
| С2Н2 СS2 NО С6Н6 С2Н4 Н2S NН3 СН4 С2Н6 НСl | г г г г г г г г г г | +226,75 +115,28 +90,37 +82,93 +52,28 -20,15 -46,19 -74,85 -84,62 -92,31 | СО СН3ОН С2Н5ОН Н2О Н2О NН4Сl СО2 Fе2О3 ТiО2 Са(ОН)2 Аl2О3 | г г г г ж к г к к к к | -110,52 -201,17 -235,31 -241,83 -285,84 -315,39 -393,51 -822,10 -943,90 -986,50 -1669,80 |
Пример 2. Реакция горения этана выражается термохимическим уравнением С2Н6(г) + 3 ½ О2 = 2 СО2(г) + 3 Н2О(ж); Нхр = -1559,87 кДж.
Вычислите теплоту образования этана, если известны теплоты образования СО2(г) и Н2О(ж) (см. табл. 5 ).
Решение. Теплотой образования (энтальпией) данного соединения называют тепловой эффект реакции образования 1 моль этого соединения из простых веществ, взятых в их устойчивом состоянии при данных условиях. Обычно теплоту образования относят к стандартному состоянию, т.е. 25 оС (298 К) и 1,013∙105 Па и обозначают через ∆Н  . Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через ∆Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
. Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через ∆Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
2С (графит) + ЗН2(г) - С2Н6(г); ∆Н= ?
исходя из следующих данных:
а) С2Н6(г) + 3'/2О2(г) = 2СО2(г) + ЗН2О(ж); ∆Н= -1559,87 кДж;
б) С (графит) + О2(г) = СО2(г); ∆Н = -393,51 кДж;
в) Н2(г) + ½ O2 = Н2О(ж); ∆Н = - 285,84 кДж.
На основании закона Гесса с термохимическими уравнениями можно оперировать так же, как и с алгебраическими. Для получения искомого результата следует уравнение (б) умножить на 2, уравнение (в) — на 3, а затем сумму этих уравнений вычислить из уравнения (а):
С2Н6 + 372О2 - 2C - 2О2-ЗН2 -3/2О2 = 2СО2 + ЗН2О -2СО2 - ЗН2О
∆Н = -1559,87 -2(-393,51)-3(-285,84) = +84,67 кДж;
∆Н = -1559,87 + 787,02 + 857,52; С2Н6 = 2С + ЗН2; ∆Н= + 84,67 кДж.
Так как теплота образования равна теплоте разложения с обратным знаком, то ∆Н 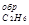 (г) = -84,67 кДж . К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
(г) = -84,67 кДж . К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
∆Нх р = 2∆НСО2 + З∆НН2О - ∆НС2н6 - 3 ½ ∆НО2
Учитывая, что теплоты образования простых веществ условно приняты равными нулю ∆Нс2н6 = 2∆НСО  + З∆НН
+ З∆НН  О - ∆Нх р
О - ∆Нх р
∆Нс2н6 = 2(-393,51) + 3(-285,84) + 1559,87 = -84,67;
то ∆Н 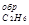 (г) = -84,67 кДж
(г) = -84,67 кДж
Пример 3. Реакция горения этилового спирта выражается термохимическим уравнением
С2Н5ОН(ж) + ЗО2(г) = 2СО2(г) + ЗН2О(ж); ∆Н= ?
Вычислите тепловой эффект реакции, если известно, что молярная теплота парообразования С2Н5ОН(ж) равна +42,36 кДж, а теплоты образования С2Н5ОН(г), СО2(г), Н2О(ж) см. табл. 5.
Решение. Для определения ∆Н реакции необходимо знать теплоту образования С2Н5ОН(ж). Последнюю находим из данных:
С2Н5ОН(ж) = С2Н5ОН(г); ∆Н= +42,36 кДж +42,36=-235,31-∆НС2Н5ОН (ж);
∆НС2Н5ОН (ж) = -235,31 - 42,36 = -277,67 кДж.
Вычисляем реакции, применяя следствия из закона Гесса:
∆Нхр = 2(-393,51) + 3(-285,84) + 277,67 = -1366,87 кДж.
Пример 4. В каком состоянии энтропия 1 моль вещества больше при одинаковой температуре: в кристаллическом или парообразном?
Решение. Энтропия есть мера неупорядоченности состояния вещества. В кристалле частицы (атомы, ионы) расположены упорядоченно и могут находиться лишь в определенных точках пространства, а для газа таких ограничений нет. Объем 1 моль газа гораздо больше объема 1 моль кристаллического вещества; возможность хаотичного движения молекул газа больше. А так как энтропию можно рассматривать как количественную меру хаотичности атомно-молекулярной структуры вещества, то энтропия 1 моль паров вещества больше энтропии 1 моль его кристаллов при одинаковой температуре.
Пример 5. Прямая или обратная реакция будет протекать при стандартных условиях в системе СН4(г) + СО2  2СО(г) + 2Н2(г)
2СО(г) + 2Н2(г)
Решение. Вычислим ∆G0298 прямой реакции. Значения ∆G0298 соответствующих веществ приведены в таблице 4. Зная, что ∆G есть функция состояния и что ∆G для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим ∆G0298 процесса: ∆G0298 = 2(-137,27) + 2(0) - (-50,79 - 394,38) = + 170,63 кДж.
То что ∆G0298 > 0, указывает на невозможность самопроизвольного протекания прямой реакции при Т = 298К и давлении взятых газов, равном 1,013 ∙105 Па (760 мм рт. ст. = 1 атм).
Таблица 4
Стандартная энергия Гиббса образования 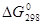 некоторых веществ
некоторых веществ
| Вещество | Состояние | 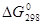 , кДж/моль , кДж/моль | Вещество | Состояние | 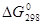 кДж/моль кДж/моль |
| ВаSО4 | К | -1138,8 | FeO | К | -244,3 |
| СаСО3 | К | -1128,75 | H2O | Ж | -237,19 |
| Fе3О4 | К | -1014,2 | H2O | Г | -228,59 |
| ВеСО3 | К | -944,75 | PbO2 | К | -219,0 |
| СаО | К | -604,2 | CO | Г | -137,27 |
| ВеО | К | -581,61 | CH4 | Г | -50,79 |
| NаF | К | -541,0 | NO2 | Г | +51,84 |
| ВаО | К | -528,4 | NO | Г | +86,69 |
| СО2 | Г | -394,38 | C2H2 | Г | +209,20 |
| NaCl | К | -384,03 | |||
| ZnO | К | -318,2 |
Таблица 5
Стандартные абсолютные энтропии 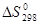 некоторых веществ
некоторых веществ
| Вещество | Состоя ние | 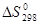 Дж/ (моль∙К) Дж/ (моль∙К) | Вещество | Состоя ние | 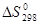 Дж/(моль∙К) Дж/(моль∙К) |
| С | алмаз | 2.44 | H2O | Г | 188,72 |
| С | Графит | 5.69 | N2 | Г | 191,49 |
| Fe | К | 27.2 | NH3 | Г | 192,50 |
| Ti | К | 30.7 | CO | Г | 197,91 |
| S | Ромб | 31.9 | C2H2 | Г | 200,82 |
| TiO2 | К | 50.3 | O2 | Г | 205,03 |
| FeO | К | 54.0 | H2S | Г | 205,64 |
| H2O | Ж | 69.94 | NO | Г | 210,20 |
| Fe2O3 | К | 89.96 | CO2 | Г | 213,65 |
| NH4Cl | К | 94.5 | C2H4 | Г | 219,45 |
| CH3OH | Ж | 126.8 | Cl2 | Г | 222,95 |
| H2 | Г | 130.59 | NO2 | Г | 240,46 |
| Fe3O4 | К | 146.4 | PCl3 | Г | 311,66 |
| CH4 | Г | 186.19 | PCl5 | Г | 352,71 |
| HCl | Г | 186.69 |
Пример 6. На основании стандартных теплот образования (см. табл. 3) и абсолютных стандартных энтропии веществ (табл. 5) вычислите ∆S0298 реакции, протекающей по уравнению СО(г) + Н2О(ж) = СО2(г) + Н2(г)
Решение. ∆G0 = ∆Н - Т∆S0; ∆Н и ∆S — функции состояния, поэтому


∆Н0х.р. = (-393,51+0) – (-110,52-285,84) = +2,85 кДж
∆S0х.р. =(213.65 + 130.59) – (197.91 + 69.94) = +79.39 = 0.07639кДж/(моль∙К)
∆G0 = +2,85 – 298 ∙ 0,07639 = - 19,91 кДж.
Пример 7.Реакция восстановления Fe2O3 водородом протекает по уравнению Fe2O3(к)+ 3H2(г) = 2Fe(к) + ЗН2О(г); ∆Н= +96,61 кДж
Возможна ли эта реакция при стандартных условиях, если изменение энтропии ∆S = 0,1387 кДж/(моль∙К)? При какой температуре начнется восстановление Fe2О3?
Решение. Вычисляем ∆G0 реакции: ∆G =∆H-T∆S = 96,61 -298 ∙ 0,1387 = +55,28 кДж.
Так как ∆G > 0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой ∆G =0:
∆Н = Т∆S; 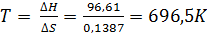
Следовательно, при температуре ≈ 696,5К начнется реакция восстановления Fe2O3. Иногда эту температуру называют температурой начала реакции.
Пример 8.Вычислите ∆Н°, ∆S и ∆G0т реакции, протекающей по уравнению Fe2O3(к) + ЗС = 2Fe + ЗСО. Возможна ли реакция восстановления Fe2O3 углеродом при 500 и 1000 К?
Решение. ∆Н0х.р. и ∆S0х.р. находим из соотношений (1) и (2):
∆Н  = [3(-110.52)+2∙0]-[-822.10+3∙0]
= [3(-110.52)+2∙0]-[-822.10+3∙0]
Энергию Гиббса при соответствующих температурах находим из соотношения
∆G500= 490,54 -500  = +219,99кДж
= +219,99кДж
∆G1000 = 490,54 - 1000  = -50.56кДж
= -50.56кДж
Так как ∆G500 >0, а ∆G1000 <0, то восстановление Fe2O3 возможно при 1000 К и невозможно при 500К.
Скорость химической реакции
Изучение скоростей реакции позволяет выяснить истинный механизм протекания сложных химических превращений. Это в свою очередь создает перспективы для нахождения путей управления химическим процессом, т.е. его скоростью и направлением. Выяснение кинетики реакций позволяет осуществить математическое моделирование реакций, происходящих в химических аппаратах, и с помощью электронно-вычислительной техники решать задачи оптимизации и автоматизации химико-технологических процессов.
Реакции могут быть гомогенными и гетерогенными. Гомогенные реакции протекают в однородной среде (например, в газовой фазе или жидком растворе). Гетерогенные реакции протекают в неоднородной среде – между веществами, которые находятся в разных фазах (твердой и жидкой, газовой и жидкой и т.д.). Таким образом, гомогенные реакции происходят равномерно во всем объеме, заполненном реагентами, гетерогенные — только на некоторых пограничных поверхностях — на границе раздела фаз. Примером гетерогенной реакции может служить реакция между веществом в газовой фазе и поверхностью жидкого или твердого тела.
Скоростью реакции называется число элементарных актов реакции, происходящих в единицу времени в единице объема (в случае гомогенных реакций) или на единице поверхности раздела фаз (в случае гетерогенной реакции). Скорость реакции обычно характеризуют изменением концентрации какого-либо из исходных или конечных продуктов реакции в единицу времени и чаще всего выражают в моль/см3∙мин.
О скорости реакции можно судить также по скорости изменения какого-либо свойства системы, например, окраски, электрической проводимости, давления, спектра и т.д.
Если в момент времени τ1 и τ2 концентрации одного из исходных веществ равны с1 и с2, то среднюю скорость υ в интервале времени τ1 и τ2 можно выразить как:

Поскольку речь идет об убыли концентрации исходного вещества, изменение концентрации в этом случае берется со знаком минус.
В ходе химических процессов концентрации веществ меняются непрерывно. Поэтому важно знать скорость реакции в данный момент времени, т.е. мгновенную скорость реакции. Последняя выражается первой производной концентрации по времени:
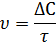
Если скорость реакции оценивается увеличением концентрации одного из продуктов реакции, то производная берется со знаком плюс.
Скорость химических превращений зависит от природы реагирующих веществ, их концентраций и внешних условий.
Скорость гомогенных реакций зависит от концентрации реагирующих веществ. Скорость реакции пропорциональна произведению концентраций реагирующих веществ, возведенных в степени их стехиометрическим коэффициентом.
Указанная закономерность называется законом действующих масс(Гульдберг и Вааге).
Для двухмолекулярной реакции взаимодействия водорода и йода Н2(г)+I2(г)=2НI(г) закон действующих масс выражается в виде следующего кинетического уравнения: 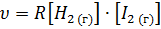 , где υ-скорость реакции; [Н2] и [I2] – концентрации соответственно Н2 и I2. Кинетическое уравнение для трехмолекулярной реакции 2NO(г) + Cl2(г) = 2NOCl (г) будет
, где υ-скорость реакции; [Н2] и [I2] – концентрации соответственно Н2 и I2. Кинетическое уравнение для трехмолекулярной реакции 2NO(г) + Cl2(г) = 2NOCl (г) будет 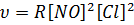
Коэффициент пропорциональности R называется константой скорости реакции. Величина R численно равна скорости реакции, когда концентрации реагирующих веществ равны единице. Константа скорости реакции зависит от: 1) природы реагирующих веществ; 2) температуры; 3) давления; 4)концентрации; 5) катализаторов.
Зависимость скорости реакции от температуры определяется правилом Вант-Гоффа, согласно которому

где υt - скорость реакции при температуре t2, до которой нагревалась или охлаждалась система; υн – скорость реакции при начальной температуре t1; ∆t=t2-t1 и γ – температурный коэффициент, т.е. число, показывающее, во сколько раз увеличивается скорость реакции при повышении температуры на каждые 10о. Значения γ при обычных температурах лежат в пределах 2-4 для большинства реакций.
Увеличение скорости реакции с повышением температуры объясняется увеличением числа так называемых активных молекул, т.е. молекул, обладающих достаточной энергией для осуществления химического взаимодействия при их столкновении. Та минимальная избыточная энергия по сравнению со средней энергией, которой должны обладать молекулы, чтобы реакция между ними стала возможной, называется энергией активации Еа.
Разница между средней энергией молекул продуктов реакций и молекул исходных веществ (Ек-Ен) определяет тепловой эффект реакции 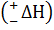 . Если Ек<Ен, то процесс будет экзотермическим, а если Ек>Ен, то эндотермическим.
. Если Ек<Ен, то процесс будет экзотермическим, а если Ек>Ен, то эндотермическим.
4.2.2. Физические методы стимулирования химических превращений
В связи с поисками новых путей проведения процессов в химической технологии разрабатываются методы направленного регулирования ре
