Энергетика химических реакций.
Энергетическая сторона реакций изучается в разделах химии, называемых термохимией и химической термодинамикой.
Термодинамикана основе энергетических критериев – термодинамических потенциалов дает ответ на вопрос: осуществим ли принципиально тот или иной химический процесс в данных условиях или нет. Изменение термодинамических потенциалов, характеризующее данный процесс, является его движущей силой. Наиболее часто в качестве движущей силы используется изменение энергии Гиббса, или изобарно-изотермического потенциала  , характеризующего переход процесса из начального в конечное состояние (реагентов, или исходных веществ, в продукты реакции) при постоянстве температуры и давления в системе:
, характеризующего переход процесса из начального в конечное состояние (реагентов, или исходных веществ, в продукты реакции) при постоянстве температуры и давления в системе:
 (1)
(1)
Если 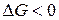 , то процесс принципиально осуществим, если
, то процесс принципиально осуществим, если  , то процесс невозможен. Чем меньше
, то процесс невозможен. Чем меньше  , тем сильнее стремление к протеканию процесса и тем дальше он от состояния равновесия, при котором
, тем сильнее стремление к протеканию процесса и тем дальше он от состояния равновесия, при котором  .
.
Изменение энергии Гиббса является результатом вклада двух факторов: энтропийного и энтальпийного.
Энтропийный фактор, характеризующий изменение энтропии системы при переходе из начального в конечное состояние
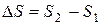 (2)
(2)
отражает стремление системы перейти от более упорядоченного состояния к менее упорядоченному, т.е., от менее вероятного к более вероятному. Значение энтропии тем выше и тем вероятнее характеризуемое ею состояние, чем большим числом микросостояний может быть представлена система. Для неупорядоченной хаотичной системы таких микросостояний огромное множество, поскольку неупорядоченность предполагает огромное количество комбинаций взаимного расположения частиц. Поэтому такая система более вероятна и характеризуется большим положительным значением энтропии. Если же система упорядочена, высокоструктурирована, то находящиеся во взаимном расположении частицы обычно жестко связаны между собой силами химического или межмолекулярного взаимодействия, не имеют достаточно степеней свободы для движения друг относительно друга с образованием новых комбинаций взаимного расположения. Поэтому число микросостояний такой системы невелико, и последняя характеризуется низким значением энтропии. Исходя из изложенного, самопроизвольность процесса определяет положительное значение изменения энтропии:  и
и  .
.
Энтальпийный фактор, характеризующий тенденцию перехода системы из более высокого энергетического состояния к менее высокому, выражается изменением энтальпии системы при переходе из одного состояния к другому:
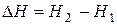 (3)
(3)
Суммарный вклад обоих факторов отражается в выражении изменения изобарно-изотермического потенциала:
 (4)
(4)
Поскольку самопроизвольность процесса определяется неравенством 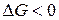 , можно видеть, что этому способствуют положительное изменение энтропии процесса
, можно видеть, что этому способствуют положительное изменение энтропии процесса  (переход системы из более упорядоченного к менее упорядоченному состоянию) и отрицательное изменение энтальпии процесса
(переход системы из более упорядоченного к менее упорядоченному состоянию) и отрицательное изменение энтальпии процесса  (переход системы из более высокого энергетического состояния к менее высокому).
(переход системы из более высокого энергетического состояния к менее высокому).
В общем случае значение  определяется совместным вкладом обоих факторов. В этом плане можно выделить 4 случая.
определяется совместным вкладом обоих факторов. В этом плане можно выделить 4 случая.
1)  ,
,  . В этом случае процесс осуществим при любой температуре.
. В этом случае процесс осуществим при любой температуре.
2)  ,
,  . В этом случае процесс термодинамически запрещен (
. В этом случае процесс термодинамически запрещен (  ) во всем диапазоне условий (самопроизвольно будет протекать обратный процесс).
) во всем диапазоне условий (самопроизвольно будет протекать обратный процесс).
3)  ,
,  . В этом случае самопроизвольность процесса определяется балансом двух факторов. Самопроизвольному процессу соответствует условие
. В этом случае самопроизвольность процесса определяется балансом двух факторов. Самопроизвольному процессу соответствует условие 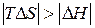 , которому отвечает диапазон температур
, которому отвечает диапазон температур  . Можно видеть, что такая ситуация реализуется в области высоких температур, нижний предел которых определяется значением
. Можно видеть, что такая ситуация реализуется в области высоких температур, нижний предел которых определяется значением 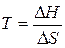 .
.
4)  ,
,  . Как и в предыдущем случае, самопроизвольность процесса определяется балансом энтропийного и энтальпийного факторов. В частности, в соответствии с требованием
. Как и в предыдущем случае, самопроизвольность процесса определяется балансом энтропийного и энтальпийного факторов. В частности, в соответствии с требованием 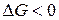 самопроизвольный характер процесса определяется неравенством
самопроизвольный характер процесса определяется неравенством  , которому отвечает диапазон температур
, которому отвечает диапазон температур 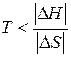 . Такая ситуация реализуется в области низких температур, верхний предел которых определяется значением
. Такая ситуация реализуется в области низких температур, верхний предел которых определяется значением 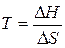 .
.
Из положений (1), (2), (3)) следует, что значения  ,
,  и
и  определяются конечным и начальным состоянием системы. Это открывает возможность их определения на основе данных, характеризующих начальное и конечное состояния систем. Для химической реакции
определяются конечным и начальным состоянием системы. Это открывает возможность их определения на основе данных, характеризующих начальное и конечное состояния систем. Для химической реакции
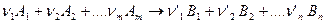 (5)
(5)
изменение энтропии в стандартных условиях (298К, 101,3кПа) определяется равенством:
 (6)
(6)
где 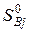 и
и 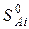 – энтропии j-го и i-го реагента соответственно в стандартных условиях.
– энтропии j-го и i-го реагента соответственно в стандартных условиях.
Значения энтропий различных простых и сложных веществ табулированы в соответствующих справочниках.
Энтальпия процесса (изменение Н) для реакции (5) определяется выражением:
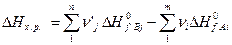 (7)
(7)
где  и
и 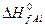 – теплоты образования j-го продукта и i-го реагента из простых веществ в стандартных условиях.
– теплоты образования j-го продукта и i-го реагента из простых веществ в стандартных условиях.
Изменение изобарно-изотермического потенциала для реакции (5) определяется выражением:
 (8)
(8)
где 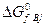 и
и  – изменения изобарно-изотермических потенциалов при образовании продуктов реакции и реагентов из простых веществ в стандартных условиях.
– изменения изобарно-изотермических потенциалов при образовании продуктов реакции и реагентов из простых веществ в стандартных условиях.
Очевидно, что движущая сила процесса ( 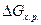 ) может быть рассчитана по формуле (8), если есть прямые данные по
) может быть рассчитана по формуле (8), если есть прямые данные по  . Если же такие данные отсутствуют, то сначала рассчитываются
. Если же такие данные отсутствуют, то сначала рассчитываются  и
и  , а затем по уравнению (4) определяют
, а затем по уравнению (4) определяют 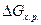 .
.
Значения  и
и  различных сложных веществ приведены в соответствующих справочниках.
различных сложных веществ приведены в соответствующих справочниках.  и
и  простых веществ равны нулю.
простых веществ равны нулю.
Раздел термодинамики, изучающий тепловые эффекты химических реакций и способы их расчета, называется термохимией.
Теплота химической реакции влияет на энергетическое состояние системы и может иметь важное значение при выборе условий протекания той или иной реакции. Как будет показано ниже, при постоянстве температуры и давления теплота реакции равна энтальпии процесса 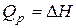 и, таким образом, отражает вклад энергетического фактора в изменение изобарно-изотермического потенциала.
и, таким образом, отражает вклад энергетического фактора в изменение изобарно-изотермического потенциала.
В соответствии с законом сохранения энергии (первый закон термодинамики) теплота, полученная системой, идет на изменение ее внутренней энергии 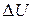 и на совершение работы А:
и на совершение работы А:
 (9)
(9)
Как G и H, внутренняя энергия является функцией состояния системы, и поэтому ее изменение определяется конечным и начальным состоянием:
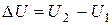 (10)
(10)
Теплота и работа не являются функциями состояния, так как они являются формами передачи энергии и связаны с процессом, а не с состоянием системы.
В химических реакциях А – работа против внешнего давления, т.е. в первом приближении 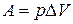 , где
, где  – изменение объема системы
– изменение объема системы  .
.
Так как большинство химических реакций протекает при постоянном давлении, то для изобарно-изотермического процесса ( 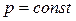 ,
, 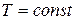 ), теплота реакции будет равна
), теплота реакции будет равна
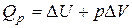 | |
| или | 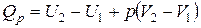 |
| и | 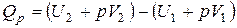 (11) (11) |
Сумма  называется энтальпией процесса (Н). Из выражения (11) следует, что теплота процесса в условиях постоянства температуры и давления приобретает свойства функции состояния, т.е. не зависит от пути, по которому протекает процесс, и равна изменению энтальпии системы
называется энтальпией процесса (Н). Из выражения (11) следует, что теплота процесса в условиях постоянства температуры и давления приобретает свойства функции состояния, т.е. не зависит от пути, по которому протекает процесс, и равна изменению энтальпии системы
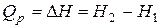
Таким образом, энтальпия является функцией состояния, поскольку ее изменение определяется только начальным и конечным состоянием системы. Нетрудно видеть, что теплота реакции в изохорно-изотермическом процессе (V = const, 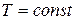 ), при котором
), при котором  , равна изменению внутренней энергии системы:
, равна изменению внутренней энергии системы:
 (12)
(12)
Теплоты химических процессов, протекающих при 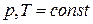 и
и  , называются тепловыми эффектами.
, называются тепловыми эффектами.
Расчеты тепловых эффектов основаны на следствии из закона Гесса: тепловой эффект химической реакции равен разности между суммой теплот образования продуктов реакции и суммой теплот образования исходных веществ с учетом стехиометрических коэффициентов перед формулами этих веществ в уравнении реакции.
Количественно расчет тепловых эффектов химических реакций представляется формулой (7). Особенностями расчетов по этому уравнению являются:
– в уравнении (7) значение 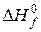 соответствует тому агрегатному состоянию, в котором реагент или продукт реакции входит в стехиометрическое уравнение (5);
соответствует тому агрегатному состоянию, в котором реагент или продукт реакции входит в стехиометрическое уравнение (5);
– коэффициенты уравнения (7) могут быть дробными, если требуется определить тепловой эффект на моль одного из продуктов реакции или реагентов.
В соответствии с законом Гесса тепловой эффект сложного процесса равен сумме тепловых эффектов его стадий. Так, образование оксида углерода (IV) из графита и кислорода можно рассматривать как результат непосредственного взаимодействия простых веществ
 ,
,  (13)
(13)
или как результат процесса, протекающего через промежуточную стадию образования и сгорания оксида углерода (II)
 ,
,  (14)
(14)
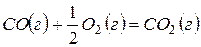 ,
, 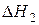 (15)
(15)
Суммируя уравнения (14) и (15), имеем
 ,
, 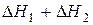 (16)
(16)
Сопоставляя уравнение (13) и (16), имеем  .
.
Примеры решения типовых задач
Пример 1. Вычисление тепловых эффектов химических реакций по значениям теплот образования реагентов и продуктов реакции.
Задача 1. Рассчитайте тепловой эффект реакции  , если значения теплот образования реагентов и продуктов составляют:
, если значения теплот образования реагентов и продуктов составляют:
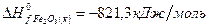

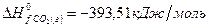
Решение. В соответствии со следствием из закона Гесса

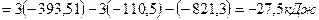
Ответ:  .
.
Пример 2. Вычисление изменения внутренней энергии.
Задача 1. Определите изменение внутренней энергии при испарении 46,8г бензола при 20оС. Теплота испарения бензола при этой температуре составляет 30,92 кДж/моль. Пары бензола подчиняются законам идеальных газов.
Решение. Изменение внутренней энергии и тепловой эффект процесса связаны между собой соотношением
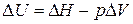 .
.
В соответствии с уравнением Менделеева-Клапейрона: 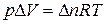 , тогда
, тогда
 ,
,
где  – изменение числа моль газообразных веществ в результате процесса.
– изменение числа моль газообразных веществ в результате процесса.
Для процесса испарения бензола
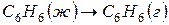
 , теплота испарения бензола равна 30,92кДж/моль, то есть,
, теплота испарения бензола равна 30,92кДж/моль, то есть,  . Тогда изменение внутренней энергии при испарении 1 моль бензола
. Тогда изменение внутренней энергии при испарении 1 моль бензола
 .
.
Число моль бензола составляет
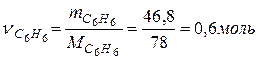 .
.
Тогда изменение внутренней энергии при испарении 48,6г бензола составляет  .
.
Пример 3. Определение теплового эффекта реакции на основе тепловых эффектов отдельных стадий процесса.
Задача 1. Даны три уравнения химических реакций:
(1) 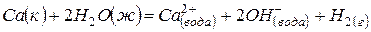 ,
, 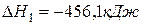
(2) 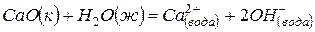 ,
, 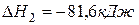
(3)  ,
, 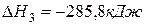 .
.
Определите тепловой эффект реакции 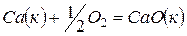 .
.
Решение. Любая сложная химическая реакция может быть представлена как алгебраическая сумма ее отдельных стадий. Нетрудно заметить, что реакция 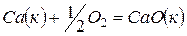 представляет собой результат комбинаций трех стадий (1) – (2) + (3). Тогда
представляет собой результат комбинаций трех стадий (1) – (2) + (3). Тогда
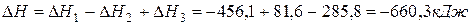 .
.
Пример 4. Расчет тепловых эффектов на основе энергий химических связей. Оценка энергий химических связей на основе теплового эффекта химической реакции с учетом энергии других разрывающихся и образующихся в химической реакции связей.
Задача 1. Рассчитайте энергию химической связи в молекуле HBr, если известны тепловой эффект реакции  ,
, 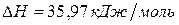
и энергии диссоциации молекул Н2 и Br2 .
Решение. Предположим, что процесс протекает через стадии диссоциации реагентов и образование молекулы HBr. Этот процесс можно представить совокупностью следующих стадий:
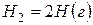 ,
, 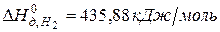
 ,
, 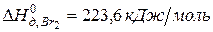
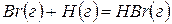 ,
, 
 |
 ,
, 
В соответствии с законом Гесса
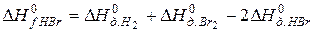
откуда: 
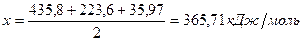
Таким образом, энергия связи HBr 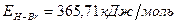 .
.
Пример 5. Определение знака изменения энтропии на основе структуры исходного и конечного состояний системы.
Задача 1. Как изменяется энтропия процесса таяния льда?
Решение. Изменение энтропии этого процесса характеризует величина
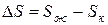
Кристаллическое состояние характеризуется высокой упорядоченностью, обусловленной структурой кристаллической решетки, в которой атомы жестко связаны между собой и имеют ограниченное число степеней свободы. Такая структура может быть представлена малым числом микросостояний. В жидком состоянии молекулы имеют большую свободу движений относительно друг друга, что обусловливает образование значительно большего числа комбинаций взаимного расположения молекул (микросостояний). Поэтому такое состояние имеет большие значения S, чем кристаллическое состояние, т.е. 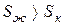 . Это приводит к положительному изменению энтропии.
. Это приводит к положительному изменению энтропии.
Пример 6. Определение знака изменения энтропии процесса на основе строения реагентов и продуктов реакции.
Задача 1. Как изменится энтропия процесса гидрирования фенола
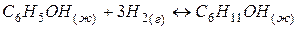
Решение. Как и в предыдущем примере  процесса определяется разностью энтропий конечного и исходного состояний
процесса определяется разностью энтропий конечного и исходного состояний
 (1)
(1)
Из двух структур C6H11OH и C6H5OH первая является более высокоорганизованной, поскольку заключает в себе большее количество химических связей и большее число структурных единиц (атомов). Поэтому  . Кроме того, второй реагент является газом, молекулы которого автономны и имеют бесчисленное множество микросостояний, поэтому
. Кроме того, второй реагент является газом, молекулы которого автономны и имеют бесчисленное множество микросостояний, поэтому  . Все это обусловливает в соответствии с (1) уменьшение энтропии при реализации процесса.
. Все это обусловливает в соответствии с (1) уменьшение энтропии при реализации процесса.
Пример 7. Выявление возможности протекания химической реакции по величине изменения энергии Гиббса.
Задача 1. В каком направлении будет протекать реакция 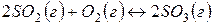 в стандартных условиях?
в стандартных условиях?
Решение. Изменение энергии Гиббса в данной реакции характеризуется равенством

Поскольку  , то в стандартных условиях данная реакция может протекать в сторону образования
, то в стандартных условиях данная реакция может протекать в сторону образования  .
.
Пример 8. Вычисление изменение энергии Гиббса в химической реакции по значениям теплот образования и энтропий реагирующих веществ и продуктов реакции.
Задача 1. Вычислите изменение энергии Гиббса  для химической реакции
для химической реакции  . Возможно ли протекание этой реакции в стандартных условиях?
. Возможно ли протекание этой реакции в стандартных условиях?
Решение. Воспользуемся для решения поставленных задач значениями теплот образования и энтропий реагентов и продуктов реакции:
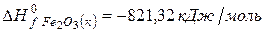

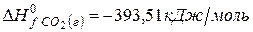
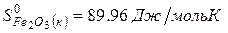



Изменение энергии Гиббса в химической реакции при температуре Т можно рассчитать по уравнению
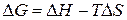 .
.
 рассчитываем на основе следствия из закона Гесса (см. ур-е 7):
рассчитываем на основе следствия из закона Гесса (см. ур-е 7):
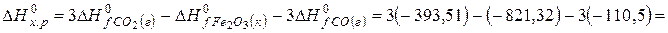
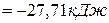 .
.
Изменение энтропии в соответствии с уравнением (6) выражается равенством:

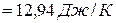 .
.
Изменение энергии Гиббса в химической реакции равно
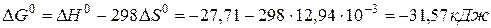
Из результатов расчета (  ) следует, что в стандартных условиях реакция осуществима.
) следует, что в стандартных условиях реакция осуществима.
1.5. Химическая кинетика и равновесие
Кинетика – раздел химической науки, изучающий скорости химических реакций и факторы, влияющие на скорость реакций.
Термодинамика на основе значений 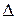 G или других критериев дает ответ на вопрос принципиальной осуществимости того или иного процесса. Но она не может ответить на вопрос, насколько быстро может быть осуществлен переход в термодинамически выгодном направлении. Если этот переход характеризуется бесконечно большим временем, то такой процесс невыгодно осуществлять в данных условиях и необходимо использовать факторы, которые бы его интенсифицировали. Например, реакция окисления водорода
G или других критериев дает ответ на вопрос принципиальной осуществимости того или иного процесса. Но она не может ответить на вопрос, насколько быстро может быть осуществлен переход в термодинамически выгодном направлении. Если этот переход характеризуется бесконечно большим временем, то такой процесс невыгодно осуществлять в данных условиях и необходимо использовать факторы, которые бы его интенсифицировали. Например, реакция окисления водорода
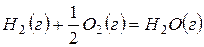
без каких-либо внешних воздействий не протекает в стандартных условиях, несмотря на его термодинамическую выгодность (  ). Внесение в такую систему катализатора, платиновой черни, приводит к мгновенному взаимодействию – взрыву. Этот результат можно проиллюстрировать нижеследующей энергетической диаграммой (рис.1).
). Внесение в такую систему катализатора, платиновой черни, приводит к мгновенному взаимодействию – взрыву. Этот результат можно проиллюстрировать нижеследующей энергетической диаграммой (рис.1).
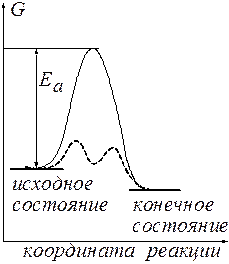
Рис.1 Энергетическая диаграмма реакции.
Можно видеть, что  имеет отрицательное значение, обусловливающее осуществимость этого процесса. В то же время энергетический барьер ЕА, который должна преодолеть реакция, достаточно высок. Такой барьер трудно преодолеть, что и выражается в бесконечно низкой скорости реакции. Если использовать в этом процессе катализатор, то с его помощью реакция начинает протекать по новому энергетическому руслу (пунктирная линия). Можно видеть, что барьеры, которые должна преодолевать система, проходя через это русло, существенно ниже, и ее собственного энергетического запаса хватает, чтобы с лихвой их преодолеть. Это находит свое выражение в резком ускорении реакции.
имеет отрицательное значение, обусловливающее осуществимость этого процесса. В то же время энергетический барьер ЕА, который должна преодолеть реакция, достаточно высок. Такой барьер трудно преодолеть, что и выражается в бесконечно низкой скорости реакции. Если использовать в этом процессе катализатор, то с его помощью реакция начинает протекать по новому энергетическому руслу (пунктирная линия). Можно видеть, что барьеры, которые должна преодолевать система, проходя через это русло, существенно ниже, и ее собственного энергетического запаса хватает, чтобы с лихвой их преодолеть. Это находит свое выражение в резком ускорении реакции.
Уравнение скорости необратимой химической реакции
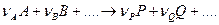
может быть выражено в следующей форме:
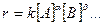 (1)
(1)
где :
k – константа скорости, определяемая как величина скорости при единичных концентрациях реагентов [А]= 1 моль/л, [В]= 1 моль/л и т.д.;
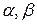 – частные порядки реакции по соответствующим реагентам А, В и др., определяющие степень влияния этих реагентов на скорость реакции;
– частные порядки реакции по соответствующим реагентам А, В и др., определяющие степень влияния этих реагентов на скорость реакции;
Сумма частных порядков реакции 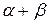 +… называется общим порядком реакции.
+… называется общим порядком реакции.
Уравнение (1) в концентрированном виде включает в себя действие различных факторов. К таким факторам относятся:
· концентрация реагентов;
· давление;
· температура;
· катализатор.
Концентрация реагентов является фактором ускорения химических реакций, поскольку, как правило, порядки реакции имеют положительное значение. Физически это легко объяснимо: с ростом концентрации возрастает количество молекул реагентов в единице объема, а следовательно, вероятность их столкновений, приводящих к химическому взаимодействию.
Давление выступает в качестве фактора ускорения процесса, когда реагент является газом. Так, если мы имеем дело с реакцией газообразных реагентов, то к каждому из них применимы газовые законы  .
.
Из последнего выражения следует, что
 (2)
(2)
Поскольку 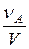 по определению концентрация реагента А, а рА по закону Дальтона линейно зависит от общего давления
по определению концентрация реагента А, а рА по закону Дальтона линейно зависит от общего давления 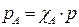 , то выражение (2) приобретает вид:
, то выражение (2) приобретает вид:
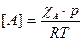 ,
,
где: 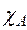 – мольная доля компонента А в газовой смеси. Значение
– мольная доля компонента А в газовой смеси. Значение  можно считать постоянной величиной и тогда
можно считать постоянной величиной и тогда
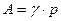 ,
,
где 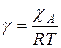 .
.
Таким образом, увеличение давления приводит к росту концентрации газообразных реагентов и в этой связи выступает как фактор скорости процесса.
Если реакционная система представляет собой систему газ – жидкость, то увеличение парциального давления газообразного реагента в соответствии с законом Генри приводит к увеличению его растворимости в жидкой реакционной массе, где, как правило, протекает реакция. Таким образом, и в этом случае давление выступает в качестве фактора увеличения концентрации реагента и, соответственно, фактора скорости процесса.
Влияние температуры на скорость реакции связано с ее влиянием на константу скорости. Основное уравнение, иллюстрирующее это влияние – уравнение Аррениуса:
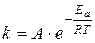 (3)
(3)
где:
А – предэкспоненциальный множитель;
ЕА – энергия активации, имеющая смысл минимального избытка энергии, которым должна обладать реагирующая частица по сравнению с их средней энергией, чтобы прореагировать.
Ускоряющее действие температуры физически обосновывается увеличением с ростом температуры доли частиц, обладающих минимальным избытком энергии ЕА, гарантирующим им преодоление энергетического барьера.
Другое, менее строгое выражение для температурного влияния на скорость химической реакции – уравнение Вант-Гоффа:
 (4)
(4)
где:
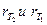 – скорости реакции при температуре Т2 и Т1 соответственно;
– скорости реакции при температуре Т2 и Т1 соответственно;
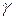 – коэффициент Вант-Гоффа, показывающий, во сколько раз увеличивается скорость реакции при повышении температуры на 10оС.
– коэффициент Вант-Гоффа, показывающий, во сколько раз увеличивается скорость реакции при повышении температуры на 10оС.
Действие катализатора как фактора ускорения процесса рассматривалось выше. Смысл ускоряющего действия катализатора – понижение энергетического барьера реакции (ЕА).
Реакции, в которых по мере накопления продуктов реакции последние вступают во взаимодействие между собой с образованием исходных реагентов, называются обратимыми.
По мере протекания этих реакций система приближается к состоянию равновесия, в котором скорости прямой и обратной реакций равны. Если на систему в состоянии равновесия не действуют какие-либо внешние факторы, то это состояние остается неизменным бесконечно долгое время и характеризуется постоянством состава реакционной массы.
Для обратимой химической реакции
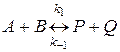
состояние равновесия определяется равенством скоростей прямой и обратной реакций

Из последнего выражения следует, что
 (5)
(5)
Поскольку является константой, то правая часть уравнения (5) также будет постоянной величиной, отражающей неизменность состава реакционной массы в состоянии равновесия. Величина 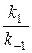 =К называется константой равновесия, характеризующей состояние системы в условиях равновесия.
=К называется константой равновесия, характеризующей состояние системы в условиях равновесия.
В стандартных условиях для обратимой реакции имеет место соотношение
 (6)
(6)
Руководствуясь этим соотношением и рисунком 1, можно показать, что катализатор, ускоряя прямую и обратную реакции, лишь ускоряет достижение равновесия, не влияя на его положение. Действительно, и в каталитической и в некаталитической реакции 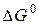 не меняется, а следовательно не меняется и К и, соответственно, состав системы в состоянии равновесия.
не меняется, а следовательно не меняется и К и, соответственно, состав системы в состоянии равновесия.
Принцип смещения равновесия (принцип Ле–Шателье) определяет направление смещения равновесия под действием различных факторов:
Если на систему, находящуюся в состоянии равновесия, оказывается внешнее воздействие, то равновесие смещается в сторону процесса, ослабляющего это воздействие.
Примеры решения типовых задач.
Пример 1. Влияние концентрации реагента на скорость химической реакции.
Задача 1. Определите скорость реакции 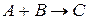 по реагентам А и В, если при увеличении концентрации вещества А в 4 раза скорость реакции возрастает в 2 раза, а концентрации В в 4 раза – в 4 раза.
по реагентам А и В, если при увеличении концентрации вещества А в 4 раза скорость реакции возрастает в 2 раза, а концентрации В в 4 раза – в 4 раза.
Решение. Скорость реакции можно выразить уравнением
 (7)
(7)
В условии варьирования концентрации А концентрация В постоянна. Тогда уравнение (7) приобретает вид
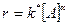 (8)
(8)
где  .
.
При увеличении [А] в 4 раза его новая концентрация составит 4[А]. Тогда скорость реакции для этих разных концентраций в соответствии с уравнение (8) выразится уравнениями:
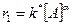 (9)
(9)
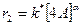 (10)
(10)
Поделив почленно левые и правые части уравнений скорости (9) и (10), имеем
 .
.
Так как  , то
, то 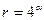 , откуда
, откуда 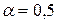 .
.
Порядок по [В] определяется в условиях постоянства концентрации [А]. Тогда
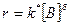 , где
, где 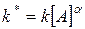 .
.
При увеличении концентрации [В] в 4 раза имеем соотношение скоростей реакции
 .
.
Так как  , то
, то 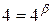 , откуда имеем
, откуда имеем  .
.
Окончательный вид кинетического уравнения:  .
.
Пример 2. Выявление роли давления как фактора скорости реакции.
Задача 1. Во сколько раз увеличится скорость элементарной реакции 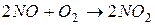 при увеличении давления в системе в 3 раза?
при увеличении давления в системе в 3 раза?
Решение.Скорость этой реакции можно выразить уравнением
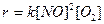 . (11)
. (11)
В соответствии с уравнением Менделеева-Клапейрона
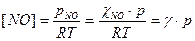 . (12)
. (12)
Аналогично
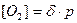 (13)
(13)
Подставляя (12) и (13) в уравнение (11), имеем
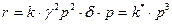 (14)
(14)
где 
При увеличении давления в 3 раза скорость реакции в соответствии с уравнением (14) составит
 (15)
(15)
Сравнивая (14) и (15), видим, что скорость реакции при увеличении давления в 3 раза увеличивается в 27 раз.
Пример 3. Влияние температуры на скорость реакции.
Задача 1. Вычислите, во сколько раз увеличится скорость реакции при повышении температуры от 30оС до 70оС, если температурный коэффициент реакции равен 2?
Решение.В соответствии с уравнением Вант-Гоффа
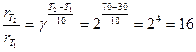 .
.
При повышении температуры на 40о скорость реакции увеличится в 16 раз.
Пример 4. Определение времени протекания реакции в зависимости от температуры.
Задача 1. При 393К реакция завершается за 10 минут. Сколько времени будет продолжаться реакция при 363К, если температурный коэффициент этой реакции равен3?
Решение.В соответствии с уравнением Вант-Гоффа

Поскольку между скоростью реакции и временем ее протекания существует обратно пропорциональная зависимость, то

Подставляя в левую часть уравнения Вант-Гоффа вместо 
 имеем
имеем
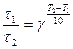 , откуда
, откуда
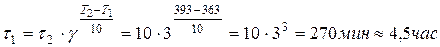 .
.
При температуре 363К реакция закончится за 4,5 часа.
Пример 5. Влияние температуры на константу скорости.
Задача 1. Во сколько раз увеличится скорость реакции при повышении температуры от 30о до 60о, если ее энергия активации составляет 80 кДж/моль?
Решение. Скорость реакции можно представить кинетическим уравнением
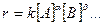
При сопоставлении скоростей реакции при разных температурах имеем
 .
.
В соответствии с уравнением Аррениуса
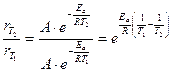 .
.
Подставляя значения 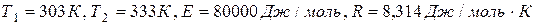 в последнее выражение, имеем
в последнее выражение, имеем

Пример 6. Вычисление равновесных концентраций реагирующих веществ.
Задача 1. Реакция протекает по уравнению 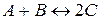 . Определите равновесные концентрации реагирующих веществ, если исходные концентрации веществ А и В соответственно равны: 4 и 6 моль/л, константа равновесия К = 1.
. Определите равновесные концентрации реагирующих веществ, если исходные концентрации веществ А и В соответственно равны: 4 и 6 моль/л, константа равновесия К = 1.
Решение.К моменту равновесия концентрации веществ А и В понизятся, а концентрация вещества С увеличится. На каждый моль вещества А и В образуется 2 моль вещества С. Поэтому если понижение концентрации вещества А и В обозначить через х моль, то увеличение концентрации вещества С будет 2х моль.
Тогда равновесные концентрации реагирующих веществ:
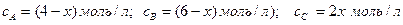
В соответствии с выражением для константы равновесия
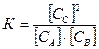 имеем
имеем  , откуда
, откуда  .
.
Решение этого уравнения дает значение х=1,62.
Отсюда равновесные концентрации реагирующих веществ равны:
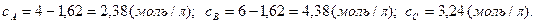
Пример 7. Влияние изменения концентрации реагирующих веществ на смещение равновесия.
Задача 1. В результате протекания химич
