Лекция № 2. Основные положения квантово-механической теории строения атома

В основе квантово-механической теории строения атома лежит планетарная модель Э. Резерфорда, согласно которой атом состоит из положительно заряженного ядра и вращающихся вокруг него электронов (электронной оболочки). Размеры ядра (» 10^-14 м) намного меньше размеров самого атома (» 10^-10 м). Согласно современным представлениям, ядро атома состоит из элементарных частиц двух видов - протонов и нейтронов (нуклонов). Протон (p) - положительно заряженная элементарная частица с массой покоя, равной 1,673·10^-27 кг (1,00782 а.е.м.), нейтрон (n) электронейтрален и имеет массу покоя 1,675·10^-27 кг (1,00867 а.е.м.). Электрон значительно легче (масса покоя составляет 9,109·10^-31 кг или 0,000549 а.е.м.) и заряжен отрицательно. Число протонов в ядре равно его заряду и, соответственно, порядковому номеру элемента в периодической системе. Число нейтронов в ядре атома одного и того же элемента может отличаться. В связи с этим один и тот же элемент обычно представлен разными изотопами. Изотопы - это атомы одного элемента, имеющие одинаковый заряд ядра, но разную массу. Например, элемент хлор представлен в природе двумя изотопами: хлор-35 (75 мол.%) и хлор-37 (25 мол.%). Атомы обоих изотопов содержат 17 протонов (заряд ядра атома хлора равен 17). Число нейтронов в ядре изотопа хлор-35 равно 18 (35 - 17), а в ядре изотопа хлор-37 равно 20 (37 - 17).

Основные положения современной квантово-механической теории строения электронной оболочки атома были заложены в 1924 - 1927 годах группой выдающихся физиков-теоретиков: Н. Бор, Луи де Бройль, Э. Шредингер, В. Гейзенберг, М. Планк и др. В основе данной теории лежат два постулата:

1. Принцип неопределенности (1927 г, В. Гейзенберг) - невозможно одновременно с высокой точностью определить положение электрона в пространстве (координаты) и его импульс (p = mu). Математическое выражение принципа неопределенности имеет следующий вид:

DxDp_x ³ h; DyDp_y ³ h; DzDp_z ³ h;

где h = h/2p - постоянная Дирака, h – постоянная Планка (6,625×10^-34 Дж×с).

Из приведенных соотношений следует, что чем точнее определено положение электрона, тем больше погрешность определения его импульса, т.е. скорости и направления движения. И наоборот, чем точнее определен импульс, тем больше погрешность определения координат. Действительно, при Dx ® 0 Dp_x ³ h/Dx ® ¥.

Вследствие этого в квантовой механике теряет смысл понятие траектории движения электрона и соответственно его орбиты. Электрон как бы "размазан" (делокализован) вокруг ядра, образуя электронное облако с разной плотностью на разных удалениях от ядра. Из принципа неопределенности вытекает одна из важнейших особенностей квантовой механики - модель электронной оболочки атома должна носить вероятностный характер. При этом необходимо отказаться от попыток точного определения местоположения электрона, а рассчитывать вероятность его проявления в той или иной точке околоядерного пространства.

2. Принцип корпускулярно-волнового дуализма (1924 г, Л. де Бройль) - любому движущемуся материальному объекту можно поставить в соответствие волновой процесс. Уравнение де Бройля легко выводится для электромагнитного излучения, которое одновременно можно рассматривать как волну и как поток элементарных частиц - фотонов.

Если энергия волны определяется уравнением Планка Е = hn (n - частота излучения), а энергия частицы уравнением Эйнштейна E = mc² (m - масса фотона, с - скорость света), то согласно принципу де Бройля hn = mc².

Частота излучения определяется формулой n = с/l (l -длина волны), следовательно l = h/mс.

Из принципа де Бройля вытекает вторая особенность квантовой механики - вероятность нахождения электрона в каждой точке околоядерного пространства должна подчиняться волновым законам.

Таким образом, мы вынуждены отказаться от описания параметров электронной орбиты, поскольку объекты микромира не подчиняются законам классической механики. В квантовой механике понятие орбиты заменено понятием "орбиталь". Электронная орбиталь - это область околоядерного пространства, вероятность нахождения электрона в котором существенно отличается от нуля. Важнейшими характеристиками орбитали являются граничная поверхность и функция радиального распределения вероятности нахождения электрона.

Граничная поверхность орбитали определяет ее форму. Обычно граничная поверхность выбирается таким образом, чтобы она ограничивала околоядерное пространство с вероятностью нахождения электрона 90%. Функция радиального распределения показывает вероятность нахождения электрона (W) на разных удалениях от ядра (r). Для 1s-орбитали атома водорода граничная поверхность и функция радиального распределения вероятности имеют следующий вид:

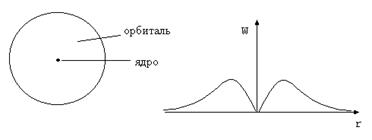
Количественно орбиталь описывается так называемой волновой Y-функцией (пси-функцией). Сама по себе волновая функция не имеет физического смысла, но квадрат ее значения в какой-то точке околоядерного пространства пропорционален вероятности нахождения электрона в бесконечно малом объеме, включающем эту точку (dV). Фактически плотность электронного облака прямо пропорциональна величине Y²dV. Изменение волновой функции, ее квадрата и вероятности обнаружения электрона (4pr²Y²) для электронной оболочки атома водорода могут быть проиллюстрированы следующим рисунком:

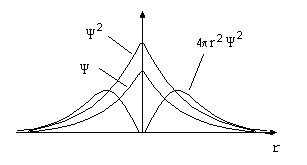
Волновые функции являются решениями волнового уравнения (1926 г., Э. Шредингер) - основного уравнения квантовой механики:

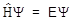
где 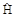- оператор полной энергии (оператор Гамильтона, гамильтониан), Е - полная энергия системы.

Кажущаяся простота уравнения исчезает при раскрытии гамильтониана, который включает кинетическую часть и потенциальную энергию электронов (U):

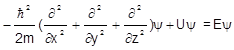
Если учесть, что сама по себе волновая функция имеет довольно сложный вид, то становится понятным, почему решение уравнения Шредингера связано с колоссальными сложностями. Строго оно может быть решено только для одноэлектронных частиц, например, для атома водорода. В то же время, решение уравнения Шредингера даже для столь простых систем привело к двум интересным следствиям:

1. Решения имеют дискретный характер и представляют собой набор волновых функций и соответствующих им дискретных (квантованных) значений энергии атома.

2. Волновые функции включают целочисленные параметры, изменяющиеся на единицу - квантовые числа. Поэтому орбитали атомы водорода можно качественно описать с помощью набора квантовых чисел. Каждое квантовое число играет важную роль, обеспечивая квантование (дискретность) определенной физической величины.

Главное квантовое число (n) - определяет энергию орбитали и среднюю удаленность электрона от ядра. Принимает значения 1, 2, 3, 4 ... ¥. Соответственно этому электронная оболочка атома разбивается на ряд энергетических уровней (K, L, M, N...), расположенных на разном удалении от ядра. Минимальную энергию имеет первый уровень. Энергия состояния, соответствующего ионизации атома (удаление электрона на бесконечное расстояние от ядра, n = ¥) принята за ноль.

Орбитальное квантовое число (l) - принимает ряд значений от 0 до n - 1 (при фиксированном n) и определяет орбитальный момент количества движения электрона, а фактически форму орбитали. Для многоэлектронных атомов l влияет также на энергию орбитали. Вследствие этого каждый энергетический уровень включает ряд подуровней с разными значениями орбитального квантового числа (0, 1, 2, 3…, соответственно, s-, p-, d-, f-подуровни) и орбиталями разной формы: s-орбитали сферической формы, p-орбитали имеют гантелевидную форму (объемная восьмерка).

Число подуровней равно номеру главного квантового числа. Так, первый уровень (n = 1) содержит один s-подуровень (l = 0). Второй уровень включает два подуровня s и p (l = 0 и 1), третий - три подуровня s, p и d (l = 0, 1 и 2), четвертый - s-, p-, d- и f-подуровни (l = 0, 1, 2 и 3).

Магнитное орбитальное квантовое число (m_l) - пробегает ряд значений от -l до +l и квантует проекцию орбитального момента количества движения электрона на одну из осей, определяя число орбиталей для каждого подуровня. s-Подуровень содержит только одну орбиталь (l = 0, m_l = 0) сферической формы.

р-Подуровень представлен тремя гантелевидными орбиталями (l = 1, m_l = -1, 0, +1), ориентированными по осям прямоугольной системы координат - p_x, p_y, p_z.

d-Подуровень содержит пять орбиталей (l = 2, m_l = -2, -1, 0, +1, +2), из которых две ориентированы по осям координат ( 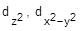), а три - по биссектрисам координатных углов (d_xy, d_xz, d_yz).

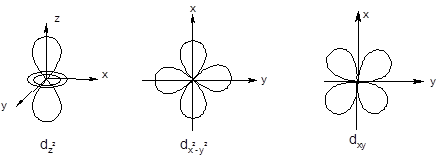
f-Подуровень содержит семь орбиталей (l = 2, m_l = -3, -2, -1, 0, +1, +2, +3) более сложной формы.

Рассмотренные квантовые числа квантуют физические характеристики электронных орбиталей как областей пространства, в которых разрешено находиться электронам. Естественно, что, заселив ту или иную орбиталь, электрон автоматически принимает ее квантовые числа. Кроме этого, электрон имеет два собственных квантовых числа - спиновое и магнитное спиновое.

4. Спиновое квантовое число (s) квантует собственный вращательный момент количества движения элементарной частицы. Для электрона s = 1/2.

5. Магнитное спиновое квантовое число (m_s) определяет проекцию собственного вращательного момента движения элементарной частицы на одну из осей и пробегает ряд значений от -s до +s. Для электрона магнитное спиновое квантовое число принимает два значения -1/2 (b-спин, ¯) и +1/2 (a-спин, ­).

Литература: [1] с. 55 - 81; [2] с. 43 - 59; [3] с. 20 - 30