Метод функціональних рівнянь.

Як показав Р. Бельман, знаходження оптимального рішення багатоетапного процесу зводиться до вирішення деякого функціонального рівняння. Роздивимося приклад багатоетапного процесу розподілу. Нехай є деяка кількість засобів х, які треба вкласти в розвиток двох неоднорідних підприємств. Відомо, якщо в перше підприємство вкласти у, а в 2-е - х - у засобів, то прибуток буде відповідно g(у) і h(х-у). Необхідно вибрати у так, щоб загальний прибуток

W1(х; у) = g(y) + h (x-y) (4.1.) був максимальний.

Таким чином, потрібно визначити max W1 (x; y)

Якщо g(y) і h(x-y) функції безперервні для х > 0, то така задача має рішення. Цей процес одноетапний.

Зауваження. х і g(y) можуть вимірюватися в різних величинах наприклад, х - грошова сума, g(y) кількість людино-годин, зекономлених у результаті застосування машин, куплених за засоби у.

Ускладнимо задачу. Розглянемо двохетапний процес. Припустимо, що за рахунок витрат, необхідних для одержання прибутку g(y), початкова кількість засобів зменшується до а. у, 0 < a < 1, аналогічно для 2-го підприємства: х-у зменшується до b(х-у), 0<b<1. Таким чином, після здійснення одноетапного процесу залишок засобів складає ау + b(х-у). Повторимо процес розподілу сумарного залишку, вважаючи, що ау + b(х-у) = х₁ = у₁ + (х₁-у₁), де 0 < y₁ < x₁. У результаті цього розподілу на 2-ом етапі одержимо прибуток g(y₁) + h(x₁-y₁), а повний прибуток за два етапи W₂(x, y, y₁) = g(y) + h(x-y) + g(y₁) + h(x₁-y₁), причому max W₂ (x, y, y₁) знаходиться по двохмірної області 0 < y < x, 0 < y₁ < x₁.

Роздивимося N-етапний процес, у якому операція розподілу повторюється послідовно N разів. Визначимо повний прибуток від цього процесу

W_N(x; y; y₁; ... ; y_N-1)=g(y)+h(x-y)+g(y₁)+h(x₁-y₁)+ ... +g(y_N-1)+h(x_N-1-y_N-1) (1.1)

де x₁ = ay + b(x-y); 0 < y < x

x₂ = ay₁ + b(x₁ - y₁) 0 < y₁ < x₁ (1.2)

x_N-1 = ay_N-2 + b(x_N-2 - y_N-2) 0 < y_N-2 < x_N-2 0 < y_N-1 < x_N-1

Одержуємо max W_N по області (1.2.), N - мірної області. Рішення такої задачі складне. Тому вирішимо задачу поетапно, наслідуючи принципу умовної оптимальності в N-етапному процесі. Визначимо функцію f_N(x) як максимум прибутку, отриманого від
N-етапного процесу, що починається з розміру х, для
N=1, 2, ..., і x > 0, тобто f_N(x) = max W_N(x; y; y₁; ... ; y_N-1) (1.3)

0<y<x

f₁(x) = max g(y) + h(x-y) (1.4)

0<y<x

Розглянемо двохетапний процес. Повний прибуток складається з прибутків 1 і 2-го етапів, причому на 2-ому етапі для розподілу залишається сума ау+b(x-y). Необхідно одержати максимальний прибуток, тому якою б не була обрана у, сума, що залишилася до наступного етапу ау + b(х-у), повинна бути використана щонайкраще (принцип умовної оптимальності), тобто від другого етапу одержимо прибуток f_1[ay + b(x-y)]. Тоді повний max прибуток за два етапи висловиться рекурентним співвідношенням

f₂(x) = max {g(y) + h(x-y) + f₁[ay + b(x-y)]} (1.5)

0<y<x

Міркуючи аналогічно, у випадку N-етапного процесу отримуємо основне функціональне рівняння

f(x) = max {g(y) + h(x-y) + f_N-1[ay + b(x-y)]} (1.6)

0<y<x

Використовуючи (1.6.) знаходимо f₁, потім f₂ і т.д., причому на кожному k-етапі одержуємо й оптимальне у_k(х).

Застосування розглянутого методу функціональних рівнянь до рішення задач Д.П. дозволяє призвести рішення однієї N-мірної задачі до послідовності однотипних рішень N одномірних задач.

Якщо врахувати, що в Д.П. процес розглядається від кінця до початку, то типове функціональне рівняння, що описує дискретний процес має вигляд

f_N(x) = max [g_N(y_N) + f_N-1(x-y_N)] (1.7)

0<y_N<x

де f - критерій процесу, N - число етапів, х - змінна, що характеризує стан процесу на N-ому етапі, f_N(x) - результуюче значення критерію, що може бути отримане за N- етапів, що залишилися, починаючи зі стану x, y_N - керуюча перемінна, від вибору якої залежить величина f_N; g_N(x_N) - величина критерію, отримана на N-ому етапі при оптимальному виборі y_N, 0<y_N<x; f_N-1 (x-y_N) - результуюче оптимальне значення критерію за N-1 етапів , що залишилися, починаючи зі стану x - y_N.

Нехай на N-ому етапі обране оптимальне рівняння y_N = y_N*. Тоді стан системи на N-1 етапі описується функціональним рівнянням

f_N-1(x-y_N*) = max [g_N-1(y_N-1) + f_N-2(x-y*-y_N-1)] (1.8)

0<y_N-1 <x-y_N*

Задача розподілу ресурсів

У розглянутої раніше задачі передбачалося, що повний прибуток залежить тільки від початкової кількості засобів і числа етапів N і не залежить від часу початку процесу. Припустимо, що в результаті розподілу засобів х на величини y і х-у на k-ому році отриманий прибуток g_k(x; y) і для подальшого розподілу залишилася кількість засобів r_k(x; y). Необхідно визначити керування, що дозволяє максимізувати повний прибуток N-етапного процесу.

Нехай ф. g_k(x; y) і r_k(x; y) неперервні для x > 0 і
0 < y < x; а r_k(x; y) у цій області 0 < r_k(x; y) < ax; а < 1 для k =1, 2.

Нехай f_k N(x) повний прибуток від N - етапного процесу, що починається з величини х на k-ом році, якщо дотримувався принцип оптимальності. Тоді при N=1

f_k1(x) = max g_k(x; y)

0<y<x

при N > 2, аналогічно міркуючи, отримаємо

f_kN(x) = max {[g_k(x;y) + f_{k+1, N-1} [r_k(x;y)]}

0<y<x

Для спрощення запису замість подвійних індексів будемо використовувати один. Положимо, що кожному етапу відповідають значення k = 1; 2; ...; N і визначимо f_k(x) як повний прибуток від процесу, що починається з величини х на k-ому етапі і закінчується на N-ому етапі, якщо дотримується принцип оптимальності. Тоді маємо такі функціональні рівняння:

при k=N

f_N(x) = max g_N(х; y) (1.9)

0<y<x

при k = N - 1, ... , 2, 1

f_k(x) = max {[g_k(x;y) + f_k+1 (r_k+1(x_k;y)] (1.10.)

0<y<x

Приклад 1.2. Для розвитку двох галузей 1 і II на 5 років виділено х засобів. Кількість засобів у, вкладених у галузь I, дозволяє одержати за один рік прибуток 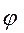(у) = у² і зменшується до розміру 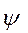(у) =0,75у. Кількість засобів х - у, вкладених у галузь II, дозволяє одержати за один рік прибуток x(х-у) = 2(х-у)² і зменшується до величини x(х-у) = 0,3 (х-у).

Необхідно так розподілити виділені ресурси між галузями по роках планованого періоду, щоб повний прибуток був максимальний.

Рішення. П'ять років розіб'ємо на 5 етапів, тобто N=5; k = 1; 2, ..., 5, хоча процес безперервний, величини х та у для наочності будемо позначати індексами.

Умовну оптимізацію почнемо з 5-го етапу, розподіляючи залишок засобів х_у. Для цього визначимо оптимальне значення у₅. Складемо вираження для (4.9.)

g₅(x₄; x₅) = 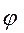(у₅) + 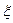(х₄-у₅) = y₅² + 2(x₄-x₅)²

f₅(x₄) = max [y₅² + 2(x₄ - y₅)²].

0<y<x

Так як для 5-го етапу х₄ є постійною величиною, то потрібно знайти max функції на відрізку [0; x₄].

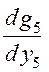= 2у₅ - 4(х₄ - у₅) = 0; у₅ = 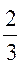х₄.

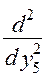= q₄ (х₄; у₅) = 6 > 0; тобто точка у₅ = 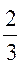х₄ точка min.

Визначимо значення ф. на кінцях: q5 (x₄; 0) = 2x₄²;

q5 (x₄; x₄) = x₄².

Одержимо, що ф. q₅ (x₄; х₅) приймає max при у₅ = 0, отже f₅(x₄) = 2x₄².

Таким чином, max прибуток на 5-ому етапі досягається при вкладенні всіх засобів, що залишилися, у II галузь.

Для 4-го етапу, використовуючи рівняння (4.10)

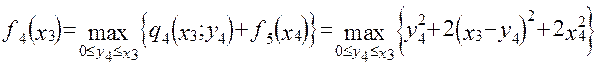
Тут х₄ - сума засобів , що залишилися, якщо на 4-ому етапі було витрачено у₄ засобів у галузі I і х₃-у₄ у галузі II.

Таким чином х₄ = 0,75у₄ + 0,3 (х₃ - у₄).

Тоді

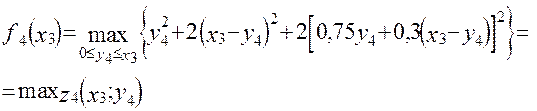
Для рішення знаходимо

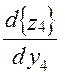= 2у₄ - 4(х₃ - у₄) + 4(0,75-0,3) [(0,75y₄ + 0,39x₃ - y₄)] = 0;

6,81 y₄ - 3,46x₃ = 0 y₄ = 0,5x₃

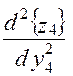= 6,81 > 0, тобто це точка min f₄(x₃) = 1,3 x₃².

Знаходимо значення z₄ на кінцях [0; x₃]

z₄(x₃; 0) = 2x₃² + 0,18x₃² = 2,18 x₃²

z₄(x₃; x₃) = x₃² + 1,125x₃² = 2,125 x₃²

Тоді max z₄ при у₄ = 0 і f₄(x₃) = 2,18 x₃²

Отже, максимальний прибуток на 4 етапі буде, якщо на його початку всі засоби, що залишилися, укласти в II галузь.

Запишемо функціональне рівняння для III-го етапу

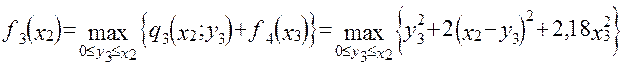
Тут х₃ - сума засобів , що залишилися після 3 етапу, якщо на 3-му етапі було витрачено у₃ засобів у галузі I і х₂-у₃ у II галузі.

х₃ = 0,75у₃ + 0,3 (х₂ - у₃).

Тоді

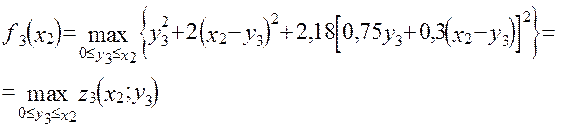
Вирішуючи його, одержуємо: у точці min z₃=0,5х₂;
z₃(x₃; 0,5х₂)=1,35x₂² при у₃=0 z₃(x₂; 0)=2,2x₂²
при у₃ = х₂ z3(x₂; x₂) = 2,23x₂²

Тоді f₃(x₂) = 2,23 x₂²

Одержимо max прибуток на 3-му етапі при вкладенні всіх засобів х₂, що залишилися у I-у галузь.

Запишемо функціональне рівняння для II-го етапу

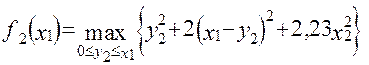
Так як х₂ = 0,75у₂ + 0,3 (х₁ - у₂), то

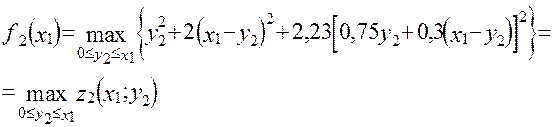
Вирішуючи це рівняння, одержуємо min z₂ = 1,36х₁²
при у₂ = 0,5х₁ z₂(x₁; 0) = 2,21 x₁²; z₂(x₁; x₁) = 2,25x₁². Отже, f₂(x₁) = =2,25 x₁²

Таким чином, для одержання max прибутку на 2-ому етапі всі засоби, що залишилися після І етапу вкласти в I-у галузь.

Запишемо функціональне рівняння для I-го етапу

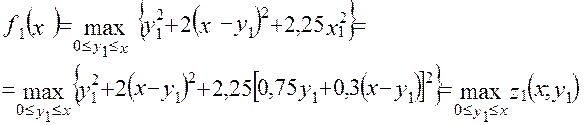
Вирішуючи, маємо: 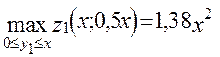z₁(x;0)=2,2x² z₁(x; x) = 2,27x²

Тобто для одержання максимального прибутку на І-ому етапі всі засоби треба вкласти в I-у галузь.

Висновок. Оптимальне керування процесом розподілу виділених засобів полягає в наступному: на протязі перших трьох років усі засоби варто вкладати тільки в I-у галузь, а на протязі останніх двох - у II галузь.

Визначимо величини засобів, що перерозподіляються для кожного етапу, з огляду на те, що знайдене оптимальне керування справедливе для x>0

I рік - усі засоби х в I галузь, залишок на початок 2-го року 0,75х

II рік - 0,75х в I-у галузь, залишок 0,75²х = 0,56х

III рік - 0,56х вкладаємо в I-у галузь, залишок 0,75*0,56х = 0,42 х

IV рік - 0,42х вкладаємо в 2-у галузь, залишок 0,42*0,3х = 0,126х

V рік - 0,126х вкладаємо в 2-у галузь, залишок
0,3*0,126х = 0,038х.

При такому розподілі max прибуток за 5 років f(x) = 2,27х².

Методом функціональних рівнянь можуть бути вирішені і більш складні задачі розподілу ресурсів.

Задача 1.3. Є деяка кількість засобів зв'язку х, яку можна використовувати N різноманітними засобами. Нехай x_i - кількість засобів, використовувана при i-ому способі розподілу (i = 1; 2; N) q_i(x_i) прибуток, отриманий у цьому випадку. Необхідно визначити, яку кількість засобів і якого засобу варто використовувати, щоб одержати максимальний загальний прибуток.

Рішення. Запишемо математичну модель задачі

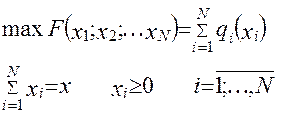
Максимальний загальний прибуток залежить тільки від Х та N. Тому можна визначити послідовність функцій

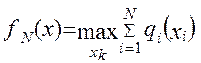для x>0 k = 1; ...; N

Одержуємо такі функціональні рівняння:

для одноетапного процесу

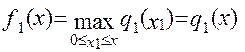(1.11)

для N - етапного процесу

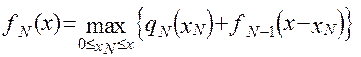N = 2; 3; ... (1.12)

Використовуючи (1.12-1.13) вирішимо задачу про завантаження літака.

Задача 1.4. Нехай є літак вантажопідіймальністю W і його варто завантажити предметами N різноманітних типів і різноманітної цінності. Необхідно завантажити літак предметами максимальної цінності, якщо відомо, що P_i - вага одного предмета i-го типу, x_i - число предметів i-го типу. C_i - вартість предмета i-го типу i = 1; ...; N.

Рішення. Складемо математичну модель задачі.

Знайти max F (x₁; x₂; ...; x_n) = 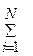C_ix_i

при 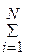Р_ix_i < W, x_i = 0; 1; 2; ...

У силу цілочисленості x_i це не задача Л.П.

Вирішимо задачу, рахуючи W - довільною величиною.

Якщо завантажувати літак тільки предметами 1-го типу, то рішення очевидно x₁ = [W/Р_i] - ціла частина. f₁(W) = [W/Р₁] . C₁

Нехай літак завантажується предметами 1-го і 2-го типів.

Позначимо max вартість у цьому випадку f₂(W).

Якщо завантажувати x₂ - предметів 2-го типу, то вага предметів 1-го типу не повинна перевищувати W₂ - P₂x₂, а їхня вартість C₂x₂.

Тоді max вартість вантажу предметів І типу - f₁(W - P₂x₂)

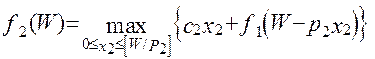
Продовжуючи процес, додаючи предмети нових типів, через N кроків

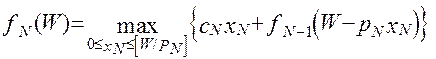
де f_N-1 (W - P_Nx_N) - максимальна вартість вантажу, що складається з предметів N-1 типу, загальна вага котрих < W - P_Nx_N.

Умови. Нехай W = 83 од., а вага і вартість предметів відповідно рівні: Р₁ = 24; Р₂ = 22; Р₃=16; Р₄=10; С₁=96; С₂=85; С₃=50; С₄=20.

Тому що для знаходження значень f_N(W) необхідно знати значення f_N-1 (W-P_Nx_N), то при рішенні будуть потрібні значення функції f(W) для всіх W 0 < W < 83.

Нехай літак завантажують тільки предметами 1-го типу. Тоді можна завантажити максимальну кількість [83/24]=3, тобто х₁ = 0; 1; 2; 3.

Тоді таблиця 1 f₁(W) має вигляд.

Таблиця 1 Таблиця 2

W	f1(W)	x1		W	f2(W)	x2	x1
0-23				0-21
24-47				22-23
48-71				24-43
72-83				44-45
				46-47
				48-67
				68-69
				70-71
				72-83

Нехай літак завантажують предметами першого і 2-го типів (2 етап) Тому що Р₂ = 22 од., то х₂ = 0; 1; 2; 3 ([W/P₂] = [83/22] = 3.

Розмір вантажопідіймальності розбиваємо на інтервали, з огляду на Р₁ і Р₂. За допомогою таблиці 1 і функціонального рівняння

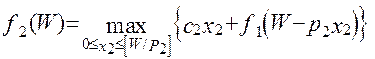
Переходимо до 3-го і 4-го етапів, що полягають відповідно в послідовному завантаженні літака предметами 1-го, 2-го, 3-го типу і 1-го, 2-го, 3-го і 4-го типу. На 3-му етапі, використовуючи таблицю 2, складаємо таблицю 3.

Таблиця 3 Таблиця 4

W	f3(W)	х3	x2	x1		W	f4(W)	х4	х3	x2	x1
0-15						0-9
16-21						10-15
22-23						16-21
24-31						22-23
32-37						24-31
38-39						32-37
40-43						38-39
44-45						40-43
46-47						44-45
48-63						46-47
64-67						48-57
68-69						58-63
70-71						64-67
72-83						68-69
						70-71
						72-81
						82-83

На підставі таблиці 4 можна зробити висновок, що max вартість завантаження вантажу 308 од., причому першого типу 3 од. і 4-го типу 1 од.

Висновок. Знайдено оптимальні рішення не тільки вантажопідіймальністю W = 83 од., але і для літаків будь-якої вантажопідіймальності 0 < W < 83 од.. Це характерна риса динамічного програмування.

Інша інтепретація задачі: стрижень довжиною W потрібно розкроїти на заготовки довжиною L₁, L₂, L₃, L₄ з вартостями відповідно, C₁, C₂, C₃, C₄, так щоб сумарна вартість була max.

Таким чином, метод Д.П. можна успішно застосовувати і для розкрою матеріалів.