Помехоустойчивое кодирование

Раздел 2 Кодирование сигналов

Основные принципы кодирования сигналов

Как правило, сообщение от источника информации представляется в аналоговой форме, т.е. непрерывными сообщениями.

Представление различных сообщений (буквы, звуки, цвета, события и т.д.) в определенной форме, например, в виде последовательности двоичных символов, называется кодированием.

Коды как средство тайнописи появились в глубокой древности. Известно, что еще древнегреческий историк Геродот в V в. до н.э. приводил примеры писем, понятных только адресату. Секретная азбука использовалась Юлием Цезарем. Над созданием различных шифров работали такие известные ученые средневековья как Ф. Бекон, Д. Кардано и др. Появлялись очень хитрые шифры и коды, которые с течением времени расшифровывались и переставали быть секретом.

Задача кодирования сообщений представляется как преобразование числовых данных в заданной системе счисления. Процесс кодирования заключается в представлении различных сообщений условными комбинациями, составленными из небольшого количества элементарных сигналов (например, посылка и пауза в коде Бодо, «точка» и «тире» в коде Морзе).

Число используемых при этом различных элементарных сигналов называют основанием кода, а число элементов, образующих кодовую комбинацию – значностью кода. Если все комбинации имеют одинаковую значность, то код равномерный. Операция кодирования применяется для цифровых сигналов. Для непрерывных сигналов требуется предварительное преобразование аналогового сигнала в цифровой.

Кодирование заключается в представлении передаваемого сигнала последовательностью простых элементов – цифр, знаков, электрических импульсов различной формы, по которым на приемной стороне можно однозначно восстановить сигнал. Устройство, выполняющее кодирование, называется кодером.

Обратное преобразование принятых сигналов в сообщение называется декодированием, а устройство - декодером. Набор отличающихся возможных значений сигнала называется алфавитом. При кодировании используется двоичная система счисления. Двоичным цифрам соответствуют два элементарных сигнала, которые технически легко сформировать. Например, одним элементарным сигналом может быть посылка напряжения (тока), вдвое превышающая помеху, а другим – отсутствие посылки.

Рисунок 2.1 – Двоичное кодирование

Помехоустойчивое кодирование

Переход на цифровые системы обработки и передачи информации создает много проблем при проектировании современных систем телекоммуникаций. Одной из важнейших задач, которые при этом необходимо решать во всех подобных системах, является обеспечение высокой достоверности передачи данных.

В связи с этим существует понятие оптимального кодирования. Под ним понимают такой код, который не только имеет в среднем наиболее короткие кодовые группы, но и полностью исключает возможность ошибок, связанных с неоднозначностью кодирования.

Под помехоустойчивостью системы связи понимают способность ее передавать сообщения в условиях помех. Различают помехоустойчивость отдельных звеньев системы связи, осуществляющих то или иное преобразование сигнала (помехоустойчивость приемника, помехоустойчивость кода, помехоустойчивость видов модуляций и т.д.).

Количество разрядов 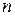в кодовой комбинации называется значностьюкода или длиной. Количество единиц в коде называют весом кодовой комбинации. Например, кодовая комбинация 1100101 характеризуется значностью 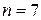и весом V = 4.

Степень отличия кодовых комбинаций характеризуется кодовымрасстоянием (хэминговым расстоянием) – 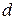. Оно выражается числом позиций, в которых комбинации отличаются, и определяется как вес суммы по модулю два кодовых комбинаций.

Под воздействием помех в разрядах возникают ошибки, т.е. 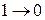, 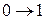. Если ошибка в одном разряде, то она называется однократной, иначе двукратной, трехкратной и т.д.

Для указания мест в кодовой комбинации, где произошли ошибки, используется понятие вектор ошибки – 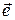. Вектор ошибки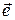 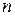-разрядного кода – это 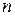-разрядная комбинация, где единицы указывают положение разрядов искаженных символов. Например, если 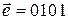, то искажены символы в нулевом и втором разрядах. Вес вектора ошибки характеризует кратность ошибки – .

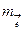Исходная неискаженная комбинация состоит из суммы по модулю 2 искаженной комбинации и вектора ошибки, т.е. .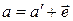

Помехоустойчивость кодов обеспечивается за счет введения избыточности, т.е. из 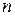общего количества символов комбинации для передачи используется только часть – m символов, при этом m<n, остальные символы контрольные - k. Таким образом, из общего числа комбинаций – 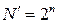– для передачи используется N=2^m разрешенных комбинаций. Группа комбинаций 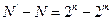называется запрещенной. Для кодирования N^’ событий требуется n=log₂N’ двоичных символов. Такой код, содержащий в себе кроме информационных разрядов еще и контрольные называется систематическим. В контрольные разряды записывается код, характеризующий состояние информационных разрядов. При этом абсолютная избыточность выражается количеством контрольных разрядов – k, а относительная избыточность отношением – k/n, где n=m+k – общее количество разрядов в кодовом сообщении.

Под корректирующими кодами понимают коды, позволяющие обнаружить и устранить ошибки, происходящие при передаче из-за влияния помех. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Если имеем n-разрядный код и вероятность искажения одного символа p, то вероятность того, что искажены k символов, а остальные n-k символов не искажены, по теореме умножения вероятностей будет 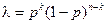. Число кодовых комбинаций, каждая из которых содержит k искаженных элементов, равна числу сочетаний из n по k:

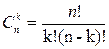. (2.1)

Тогда полная вероятность искажения кодовой комбинации будет равна:

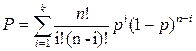. (2.2)

Так как на практике р=10^-3…10^-4, то наибольший вес в сумме вероятностей имеет вероятность искажения одного символа. Следовательно, основное внимание нужно обратить на обнаружение и исправление одиночных ошибок.

Если после приема сигнала установлено, что комбинация относится к группе разрешенных, то считается, что сигнал пришел без искажений. В противном случае сигнал считается искаженным, но это справедливо в тех случаях, когда исключена возможность перехода одних разрешенных комбинаций в другие. Следовательно, имеется N∙N’ возможных случаев передачи, из которых:

1) N случаев безошибочной передачи;

2) N(N-1) случаев перехода в другие разрешенные комбинации;

3) N(N^’-N) случаев перехода в запрещенные комбинации.

Доля обнаруживаемых ошибочных комбинаций составляет

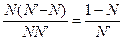(2.3)

Доля исправляемых ошибочных комбинаций от общего числа обнаруживаемых ошибок составляет:

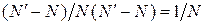. (2.4)

Избыточность кода можно ввести разными путями. Рассмотри один из путей эффективного кодирования. В ряде случаев буквы сообщений преобразуются в последовательность символов. Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии помех позволит сократить время передачи. Такое эффективное кодирование базируется на теореме Шеннона для каналов без помех, в которой доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины. Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию [3]. Следовательно, каждый символ должен принимать значения 0 или 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.

При отсутствии статистической взаимосвязи между буквами конструктивные методы построения эффективных кодов были даны впервые К. Шенноном и Н. Фано. Их методики существенно не различались, поэтому соответствующий код получил название кода Шеннона – Фано, который подробнее будет рассмотрен в разделе 2.3.1.

Рассмотрим построение кода, обнаруживающего все ошибки кратностью 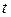и ниже. Из множества всех возможных комбинаций 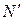нужно выбрать разрешенные комбинации 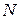так, чтобы любая из них в сумме по модулю 2 с вектором ошибки 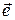с весом m_t = t не выдавала бы другой разрешенной комбинации. Для этого необходимо, чтобы кодовое расстояние удовлетворяло условию: d_min ≥ t+1. В качестве примера возьмем код со значностью n=3. Все возможные комбинации кода представлены в таблице 2.1.

Таблица 2.1.

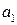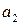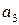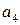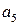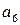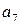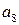Матрица расстояний между всеми возможными комбинациями имеет вид:

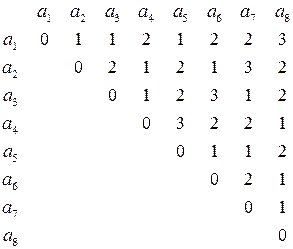
Выберем из всех возможных комбинаций разрешенные такие, чтобы d=2. Такому условию соответствуют 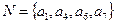. Запрещенные комбинации: а₂, а₃, а₅, а₈. Такой код позволяет обнаружить однократные ошибки.

Для обнаружения двукратных ошибок, в соответствии с условием для d_min . d=3. В этом случае, в качестве разрешенных комбинаций 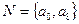, т.е. N=2.

Рассмотрим построение кода, устраняющего однократные ошибки. Возьмем в качестве разрешенной комбинации а₁=000. При наличии однократных ошибок комбинация а₁ может перейти в одну из запрещенных комбинаций а₂=001, а₃=010, а₅=100. Это означает, что в случае приема одной из них выносится решение, что передана исходная комбинация а₁ с ошибкой. При разрешенной комбинации а₄=011, при условии, что 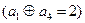и d=2, подмножество ее запрещенных комбинаций составляет: 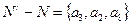, при а₃=010, а₂=001, а₈=111. Таким образом, подмножества запрещенных комбинаций для а₁ и а₄ пересеклись, имея два общих элемента а₂ и а₃, т.е. 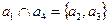. В этом случае нельзя однозначно установить исходную кодовую комбинацию.

Если же в качестве второй кодовой комбинации выбрать а₈=111, то d=3 и в случае однократных ошибок ей будет соответствовать подмножество: 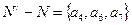при а₄=011, а₆=101, а₇=110. В этом случае подмножества не пересекаются и следовательно, обеспечивается устранение однократных ошибок.

В общем случае, для устранения ошибок кратности 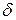кодовое расстояние должно удовлетворять условию:d_min≥2δ+1. Установлено, что для исправления всех ошибок кратности δ и обнаружения всех ошибок кратности 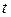( 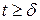), кодовое расстояние должно удовлетворять условию: d_min≥t+δ+1.

В рассмотренном примере повышение корректирующей способности кода достигалось путем уменьшения разрешенных кодовых комбинаций за счет сокращения количества информационных символов – k, т.е. k<n.

В общем, этапы построения кода сводятся к следующим.

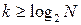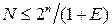1) Определение количества информационных символов исходя из объема алфавита источника информации по выражению: , где ; где 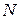– разрядность комбинации; 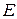– число векторов ошибок 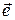, 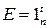– количество сочетаний из 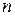по 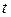. В случае устранения однократных ошибок, т.е. 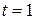, выражение для 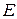и 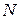имеет следующий вид: ;

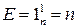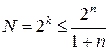. (2.5.)

2) Добавление избыточных символов для обеспечения корректирующей способности кода.

От эффективности метода кодирования, в частности от алгоритма кодирования и его реализации, зависит качество цифровой передачи данных.