Різновиди випадкових подій. Простір елементарних наслідків

ЛЕКЦІЙНЕ ЗАНЯТТЯ №1

Тема: Предмет теорії ймовірностей. Випадкові події та дії над ними.

План

1. Історична довідка.

2. Предмет теорії ймовірностей.

3. Різновиди випадкових подій. Простір елементарних наслідків.

4. Дії над подіями.

Історична довідка

Перші розробки з теорії ймовірностей (в основному азартних ігор) з’явилися вже в XVI – XVII ів. (Б. Паскаль, П. Ферма). Пізніше Я. Бернуллі, К. Гаусс. В 19 столітті теорію ймовірностей почали успішно застосовувати у страховій справі, артилерії, статистиці. Лише наприкінці 19 століття П. Чебишов та його учні А. Марков та А. Ляпунов перетворили теорію ймовірностей у математичну науку. Подальшим розвитком теорії ймовірностей зобов’язані таким математикам, як С.Берштейн, А.Колмогоров, Б.Гніденко, І.Коваленко.

Предмет теорії ймовірностей

Теорія ймовірностей – це наука про випадок, про випадкові події.

Послідовність операцій, виконуваних з додержанням певного комплексу умов, називають експериментом(дослідом, спробою). Наслідок будь-якого експерименту називають подією.

Події позначаються великими латинськими буквами A, B, C…

Наприклад,випробування— підкидання монети,

тоді події: A — «поява герба», B — «поява цифри»

Події поділяються на вірогідні, неможливі і випадкові.

Вірогідною називається подія, яка за заданих умов обов’язково станеться в даному досліді.

Наприклад, випробування — підкидання кубика, подія А — «поява на одній з граней числа, меншого за 7» є вірогідною.

Неможливою подією називається подія, яка за заданих умов не може відбутися в даному досліді. Наприклад, випробування— підкидання кубика, подія А — «поява на одній з граней числа, більшого за 6» є неможливою.

Випадковою подією називається подія, яка може відбутися, або не відбутися при певних випробуваннях. Наприклад, випробування— витягування карти з колоди, тоді подія A — «взято туза» є випадковою.

Під масовими однорідними випадковими подіями розуміють такі події, які здійснюються багатократно при однакових умовах або багато однакових подій. Якщо розглядати випадкову подію багато разів при однакових умовах, то можна виявити певну закономірність її появи чи не появи. Таку закономірність називають імовірною закономірністю масових однорідних випадкових подій.

Предметом теорії ймовірностей є вивчення імовірностних закономірностей масових однорідних випадкових подій.

Предмет математичної статистики полягає в розробці методів збору та обробки статистичних даних для одержання наукових та практичних висновків.

Різновиди випадкових подій. Простір елементарних наслідків

Дві події називаються несумісними, якщо поява однієї з них виключає появу іншої в даному досліді. Наприклад,випробування— підкидання монети один раз,

тоді події: A — «поява герба», B — «поява цифри» є несумісними.

Дві події називаються сумісними, якщо поява однієї з них не виключає появу іншої в даному досліді. Наприклад,випробування— підкидання монети два рази,

тоді події: A — «поява герба», B — «поява цифри» є сумісними.

Дві події називаються рівноможливими, якщо при виконанні даних умов однакова вірогідність появи кожної з даних подій. Наприклад, випробування — підкидання кубика, подія А — «поява числа 3» та подія В — «поява числа 2» є рівно можливими.

Дві події називаються протилежними, якщо одна і лише одна з них може здійснитися внаслідок певного випробування (позначаються А та 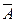). Наприклад, якщо подія A — «влучаємо в ціль при пострілі», тоді подія Ā — «промах при пострілі».

Множина подій утворює повну групу подій, якщо внаслідок кожного випробування хоч одна з цих подій напевно відбудеться.

Наприклад.Випробування — підкидання кубика,

тоді повну групу подій становлять події:

A1 — «поява 1 очка», A2 — «поява 2 очок», A3 — «поява 3 очок»,

A4 — «поява 4 очок», A5 — «поява 5 очок», A6 — «поява 6 очок»,