Описание экспериментальной установки и порядок проведения опыта
ЛАБОРАТОРНАЯ РАБОТА №4.
ИЗУЧЕНИЕ РЕЖИМОВ ТЕЧЕНИЯ ЖИДКОСТИ (ОПЫТ РЕЙНОЛЬДСА)
Цель работы: Визуально изучить качественную картину движения жидкости при ламинарном и турбулентном режимах; по опытным данным вычислить критическую скорость и критическое число Рейнольдса.
1 .Основные положения и расчетные зависимости.
При изучении движения вязкой жидкости различают два режима ламинарный и турбулентный.
Ламинарным режимом называется слоистое движение жидкости. Силы внутреннего трения или вязкости, возникающие между слоями при ламинарном движении, не дают проявиться пульсации скорости отдельных частиц и их переходу в соседние слои.
Турбулентным называется режим, при котором слоистость движения жидкости нарушена, появляется пульсация скорости, вызывающая перемешивание жидких частиц в потоке.
Характеристикой режимов движения служит безразмерное число Рейнольдса
 , (4.1)
, (4.1)
где V - средняя скорость; d. - характерный линейный размер; n-коэффициент кинематической вязкости.
Число Рейнольдса Rе, при котором происходит переход ламинарного режима в турбулентный, называется критическим - Rекр.
Ламинарный режим потока будет устойчивым при числах Рейнольлса меньших критического: для круглых труб при Reкрd=2320; для потоков некруглой формы или открытых ReкрR =580.
Экспериментально установлено, что существует два критических числа Рейнольдса: нижнее критические число Рейнольдса - Reкрн и верхнее критическое число Рейнольлса - Reкрв.
Если число Рейнольдса, подсчитанное по формуле (4.1) окажется меньше значения нижнего критического числа, т.е. Re< Reкрнто режим будет всегда ламинарным, если же Re> Reкрв то режим движения будет всегда турбулентным.
При числах Rе, удовлетворяющих неравенству
Reкрн< Re< Reкрв (4.2)
режим может быть либо ламинарным, либо турбулентным, в зависимости от предистории движения жидкости. Однако, при указанных числахRеламинарный режим движения неустойчивый, малейшие возмущения, вносимые в ламинарный поток жидкости (например, сотрясения трубы) не затухают и приводят к смене режима на турбулентный.
В отдельных случаях Reкрв может достигать 13600 и более.
Потери напора hl по длине трубы при ламинарном движении пропорциональны скорости а первой степени hl=k1V, где k1-коэффициент пропорциональности, зависящий отразмеров трубы и свойств жидкости.
При развитом турбулентном режиме потери hl пропорциональны квадрату скорости; hl=k1V2. В переходной области сопротивления (от доквадратичной к квадратичной), когда касательные напряжения в потоке от сил вязкости соизмеримы с напряжениямиот пульсаций скорости, вызывающей перемешивание, потери напора hl пропорциональны скорости в степени выше первой, но ниже второй.
Описание экспериментальной установки и порядок проведения опыта.
Существование ламинарного и турбулентного режимов движения можно проиллюстрировать опытом (вошедшим в историю как классический опыт Рейнольдса) на лабораторной установке (рис.4.1).
Для визуального наблюдения режимов течения в стеклянной трубе 1, по которой движется вода, в основной поток вводится подкрашенная струйка жидкости из сосуда 3. В качестве подкрашеннойжидкости используется слабый раствор марганца (нигрозина), подбирая его плотность приблизительно равной плотности воды во избежание гравитационного перемешивания.
Установившееся движение осуществляется поддержанием в сосуде 2 постоянного напора путем излива лишней воды. Скорость течения воды в трубе регулируется краном 4. Подкрашенная жидкость вытекает по капиллярной трубке и вводится в основной поток через иглу. Подача подкрашенной жидкости регулируется таким образом, чтобы скорости цветной струйки и воды в трубе были примерно одинаковыми.
При очень малых скоростях течения цветная струйка на всем протяжении трубы 1 не перемешивается с основным потоком. Плавным увеличением скорости от нуля до максимального значения можно уловить момент, когда подкрашенная струйка размывается и жидкость по всему сечению трубы оказывается окрашенной. Это и есть переход от ламинарного режима к турбулентному.
Опыт О.Рейнольдса является классическим примером диалектического закона перехода количества в качество. Здесь количественные изменения скорости (увеличение или уменьшение) приводят в новое качество движения (смена ламинарного режима турбулентным или турбулентного ламинарным).
Установка Рейнольдса может быть использована не только для визуального наблюдения режимов движения, но и для определения количественных зависимостей- Разность показаний пьезометров, установленных в начале и конце стеклянной трубы, определяет потерю напора на рассматриваемом участке.

Рис. 4.1. Установка дляизучения режимов движения жидкости
Для качественной оценки режимов движения жидкости необходимо провести замеры пьезометрических напоров P1/(rg), P1/(rg) по пьезометрам установленным в начале и конце стеклянного трубопровода, объем протекающей жидкости W за время t с визуальным фиксированием состояния подкрашенной струйки. Измерить температуру воды в опыте для выбора по граф.4.2 кинематическойвязкости воды. Данные измерений занести в таблицу 4.1.
Таблица 4.1
| d=….cм, tводы =….0 С, nводы=..,см2/с | |||||||||||
| Опытные данные | Расчетные данные | ||||||||||
| №№ | W | t | h1 | h2 | Режим | Q | V | hl | lgV | lghl | Rе |
| п/п | см3 | с | см | см | течения | cм3/с | см/с | см | |||
| наблюдаемый | |||||||||||
| 5,95 | ламинарное | 2,13 | 0,56 | 0,05 | -0,25 | -1,3 | 123,2 | ||||
| 5,95 | ламинарное | 3,88 | 1,02 | 0,05 | 0,008 | -1,3 | 224,4 | ||||
| 5,95 | ламинарное | 7,83 | 2,06 | 0,05 | 0,31 | -1,3 | 453,2 | ||||
| 5,95 | ламинарное | 18,02 | 4,74 | 0,05 | 0,68 | -1,3 | 1042,8 | ||||
| 5,95 | ламинарное | 25,64 | 6,75 | 0,05 | 0,824 | -1,3 | |||||
| 5,8 | турбулентное | 88,26 | 23,23 | 0,2 | 1,37 | -0,69 | 5110,6 | ||||
| 5,6 | турбулентное | 216,42 | 56,96 | 0,4 | 1,76 | -0,4 | 12531,2 | ||||
| 5,9 | 5,3 | турбулентное | 644,28 | 169,57 | 0,6 | 2,23 | -0,22 | 37305,4 |
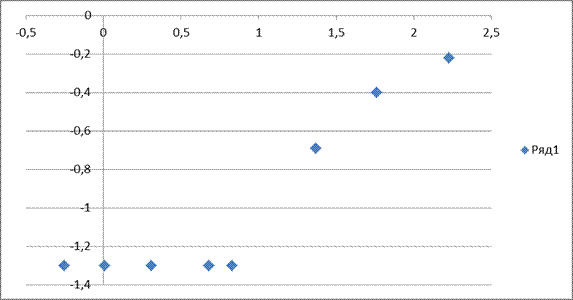
1.Изменяя расход в трубопроводе, а, следовательно, и скорость движения жидкости V, можно найти зависимость hl=f(V). Если на логарифмической сетке (рис.4.2) по оси абсцисс отложить значения скоростей, а по оси ординат - соответствующие значения потерь напора, то соединив опытные точки, получим две прямые линии аЬ и cd. Линия аЬ соответствует ламинарному режиму, а cd - турбулентному. Точка учения прямых е определяет критическую скорость течения жидкости в круглой трубе Vкр, что дает возможность определить критическое число Рейнольдса опытное Reкр.оп:
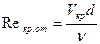
0бработка экспериментальных данных.
Используя данные таблицы 4.1. определить:
Q=W/t (4.4)
2. Скорость течения водыв трубе диаметром d=2r
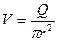 , (4.5)
, (4.5)
3. Кинематическую вязкость воды по таблицам, графикам или по формуле Пуазейля по известной температуре t в 0С:
n=0,0178/(1+0,0337t+0.000221t2), Ст (4.6)
4. Потери напора по длине трубыприz1=z2
h1-h2=hl=(P1-P2)/(rg).
5. Построить в логарифмических координатах графикзависимости hl=f(V)
6. Найти по графику hl=f(V) lgVкр критическуюскоростьVкр.
7.Определить критическое число Рейнольдса (4.3).
8.Определить относительную погрешность эксперимента.
Вывод:
Визуально изучили качественную картину движения жидкости при ламинарном и турбулентном режимах.
КОнтРОЛЬНЫЕ ВОПРОСЫ.
1. Какими характерными особенностями отличаются режимы движения?
2. Как объяснить, что потери напора при ламинарном режиме движения жидкости в трубах пропорциональны скорости в первой степени, а в турбулентном движении - во второй?
3. Чем вызвано расхождение результатов опыта и теории?
4. Ради чего в лабораторной работе поддерживается и каким образом установившееся движение жидкости?
5. От чего число Рейнольдса?
6. Как влияет температура перекачиваемой жидкости на режим движения жидкости, длина трубы, а также ее диаметр?
