Шифры сложной перестановки

В данном классе шифров перестановки используется идея многократной перестановки символов или повторного шифрования уже зашифрованного сообщения.

Шифр двойной перестановки

При шифровании шифром двойной перестановки в таблицу по определённому маршруту записывается текст, затем переставляются столбцы и строки. Далее по определённому маршруту выписывается шифрограмма.

Ключом к шифру являются размер таблицы, маршруты вписывания и выписывания, порядки перестановки столбцов и строк. Если маршруты являются фиксированными величинами, то количество ключей равно n ! m ! {\displaystyle n!m!} , где n {\displaystyle n} и m {\displaystyle m} — количество строк и столбцов в таблице[8].

ОТКРЫТЫЙ ТЕКСТ: двойная перестановка

МАРШРУТ ВПИСЫВАНИЯ: слева - направо

МАРШРУТ ВЫПИСЫВАНИЯ: сверху - вниз

СТОЛБЦЫ: ( 3, 1, 4, 2)

СТРОКИ: ( 3, 2, 4, 1, 5)

д в о й н а я п е р е с т а н о в к а

в й д о а п н я р с е е а о т н к   в а

а о т н а п н я в й д о р с е е к   в а

КРИПТОГРАММА: аавркопйстндевняоеа

Криптоанализ

При дешифровании текста используют частотные характеристики открытого текста. Однако для получения устойчивой картины длина послания должна быть существенно больше ключа. Одной из наиболее устойчивых характеристик осмысленного текста является отсутствие запретных биграмм (пара соседних букв). Например, биграммы «Ъ + Ь», «гласная + Ь», «пробел + Ь». Знание и использование частотной диаграммы открытого текста значительно упростит дешифрование шифра перестановки.

Пример (шифр Древней Спарты)

Очень удачным примером шифра перестановки является шифр Скитала(Сцитала), использовавшийся ещево времена Древней Спарты. Ключом такого шифра была цилиндрическая палочка, а шифрованиевыполнялось следующим образом:

· узкая пергаментная лента наматывалась по спирали на цилиндрическую палочку;

· шифруемый текст писался на пергаментной ленте по длине палочки, после того как длина палочкиоказывалась исчерпанной, она поворачивалась и текст писался далее, пока либо не заканчивался текст,либо не исписывалась вся пергаментная лента. В последнем случае использовался очередной кусокпергаментной ленты.

Расшифровка выполнялась с использованием палочки такого же диаметра.

Таким образом, длина блока n определялась длиной и диаметром палочки, а само шифрованиезаключалось в перестановке символов исходного текста в соответствии с длиной окружности палочки.Например, используя палочку, по длине окружности которой помещается 4 символа, а длина палочкипозволяет записать 6 символов, исходный текст: «это шифр древней спарты» превратится в шифрограмму:«эфвптрнао ер дйтшр ыиес». Длина блока n = 23, а вектор t, указывающий правило перестановки, для этогошифра может быть записан следующим образом: t = {1, 7, 13, 19, 2, 8, 14, 20, 3, 9, 15, 21, 4, 10, 16, 22, 5, 11,17, 23, 6, 12, 18}.

Шифр Вернама (англ. Verrnam Cipher) — система симметричного шифрования, изобретённая в 1917 году сотрудником AT&T Гилбертом Вернамом^[1].

Шифр является разновидностью криптосистемы одноразовых блокнотов. В нём используется булева функция «Исключающее ИЛИ». Шифр Вернама является примером системы с абсолютной криптографической стойкостью^[2]. При этом он считается одной из простейших криптосистем^[3].

История

Патент на систему Гилберта Вернама

Шифр назван в честь телеграфиста AT&T Гильберта Вернама, который в 1917 году изобрел, а в 1919 запатентовал систему автоматического шифрования телеграфных сообщений.

Вернам не использовал понятие «Исключающее ИЛИ» в патенте, но реализовал именно эту операцию в релейной логике. Каждый символ в сообщении преобразовывался побитовым XOR (исключающее ИЛИ) с ключом бумажной ленты^[4].

Вернам создал устройство, производящее указанные операции автоматически, без участия шифровальщика. Тем самым было положено начало так называемому «линейному шифрованию», когда процессы шифрования и передачи сообщения происходят одновременно. До той поры шифрование было предварительным, поэтому линейное шифрование существенно повышало оперативность связи .

Не будучи шифровальщиком, тем не менее, Вернам верно заметил важное свойство своего шифра — каждая лента должна использоваться только один раз и после этого уничтожаться. Это трудноприменимо на практике — поэтому аппарат был переделан на несколько закольцованных лент с взаимно простыми периодами^[5].

Описание

Криптосистема была предложена для шифрования телеграфных сообщений, которые представляли собой бинарные тексты, в которых открытый текст представляется в коде Бодо (в виде пятизначных «импульсных комбинаций»). В этом коде, например, буква «А» имела вид (1 1 0 0 0). На бумажной ленте цифре «1» соответствовало отверстие, а цифре «0» — его отсутствие. Секретный ключ должен был представлять собой хаотичный набор букв того же самого алфавита^[5].

Для получения шифротекста открытый текст объединяется операцией «исключающее ИЛИ» с секретным ключом. Так, например, при применении ключа (1 1 1 0 1) на букву «А» (1 1 0 0 0) получаем зашифрованное сообщение (0 0 1 0 1): {\displaystyle (11000)\oplus (11101)=(00101)} Зная, что для принимаемого сообщения имеем ключ (1 1 1 0 1), легко получить исходное сообщение той же операцией: {\displaystyle (00101)\oplus (11101)=(11000)} Для абсолютной криптографической стойкости ключ должен обладать тремя критически важными свойствами^[2]:

1. Иметь случайное равномерное распределение: {\displaystyle P_{k}(k)=1/2^{N}} , где k — ключ, а N — количество бинарных символов в ключе;

2. Совпадать по размеру с заданным открытым текстом;

3. Применяться только один раз.

Также хорошо известен так называемый шифр Вернама по модулю m, в котором знаки открытого текста, шифрованного текста и ключа принимают значения из кольца вычетов Z_m. Шифр является обобщением оригинального шифра Вернама, где m = 2^[2].

Например, кодирование шифром Вернама по модулю m = 26 (A=0,B=1,…, Z=25):

Ключ: EVTIQWXQVVOPMCXREPYZ Открытый текст: ALLSWELLTHATENDSWELL (All's well that ends well)Шифротекст: EGEAMAIBOCOIQPAJATJK

Без знания ключа такое сообщение не поддаётся анализу. Даже если бы можно было перепробовать все ключи, в качестве результата мы получили бы все возможные сообщения данной длины плюс колоссальное количество бессмысленных дешифровок, выглядящих как беспорядочное нагромождение букв. Но и среди осмысленных дешифровок не было бы никакой возможности выбрать искомую. Когда случайная последовательность (ключ) сочетается с неслучайной (открытым текстом), результат этого (шифротекст) оказывается совершенно случайным и, следовательно, лишённым тех статистических особенностей, которые могли бы быть использованы для анализа шифра.^[6].

Криптографическая стойкость[править | править вики-текст]

В 1945 году Клод Шеннон написал работу «Математическая теория криптографии» (рассекреченную только после Второй мировой войны в 1949 г. как «Теория связи в секретных системах»), в которой доказал абсолютную стойкость шифра Вернама. То есть перехват шифротекста не даёт никакой информации о сообщении. С точки зрения криптографии, невозможно придумать систему безопаснее шифра Вернама^[2]. Требования к реализации подобной схемы достаточно нетривиальны, поскольку необходимо обеспечить наложение уникальной гаммы, равной длине сообщения, с последующим её гарантированным уничтожением. В связи с этим коммерческое применение шифра Вернама не так распространено в отличие от схем с открытым ключом и он используется, в основном, для передачи сообщений особой важности государственными структурами^[5].

Недостатки

Для работы шифра Вернама необходима истинно случайная последовательность (ключ). По определению, последовательность, полученная с использованием любого алгоритма, является не истинно случайной, а псевдослучайной. То есть, нужно получить случайную последовательность не алгоритмически (а, например, используя радиоактивный распад, создаваемый электронным генератором белого шума, или другие достаточно случайные события). Чтобы сделать распределение предельно близким к равномерному, случайная последовательность обычно пропускается через хэш-функцию наподобие MD5[9].

Недостатком использования шифра Вернама является отсутствие подтверждения подлинности и целостности сообщения. Получатель не может удостовериться в отсутствии повреждений или в подлинности отправителя. Если третья сторона каким-нибудь образом узнает сообщение, она легко восстановит ключ и сможет подменить послание на другое такой же длины. Решением проблемы является применение хэш-функции. От открытого текста вычисляется хэш-функция, и её значение шифруется вместе с сообщением. При каком-либо изменении сообщения значение хэш-функции изменится. Таким образом, даже если злоумышленник заполучил шифроблокнот, не зная алгоритм вычисления хэш-функции, он не сможет использовать его для передачи информации^[8].

Под рукой всегда необходимо иметь достаточное количество ключей, которые могут понадобиться в дальнейшем для шифрования больших объёмов открытого текста. Реальный же объём текста зачастую трудно оценить заранее, в особенности это касается дипломатической и военной сферы, где ситуация способна меняться быстро и непредсказуемо. Это может приводить к нехватке ключей, что может заставить шифровальщика либо использовать ключ(и) повторно, либо полностью прервать шифрованную связь.

Проблемой является защищённая передача последовательности и сохранение её в тайне. Если существует надёжно защищённый от перехвата канал передачи сообщений, шифры вообще не нужны: секретные сообщения можно передавать по этому каналу. Если же передавать ключ системы Вернама с помощью другого шифра (например, DES), то полученный шифр окажется защищённым ровно настолько, насколько защищён DES. При этом, поскольку длина ключа та же, что и длина сообщения, передать его не проще, чем сообщение. Шифроблокнот на физическом носителе можно украсть или скопировать^[8].

Шифр Вернама чувствителен к любому нарушению процедуры шифрования. Бывали случаи, когда одна и та же страница блокнота по различным причинам применялась дважды. Например, среди всего объёма советской шифрованной переписки, перехваченной разведкой США в 40-х годах прошлого века, были обнаружены сообщения, закрытые дважды использованной гаммой. Период этот длился не очень долго, потому что уже после первых успехов американских криптоаналитиков в конце 1940-х годов в спецслужбах СССР узнали о серьёзных проблемах с надёжностью своей шифропереписки. Такие сообщения были расшифрованы в течение 40 последующих лет в рамках секретного проекта «Venona», документы которого были не так давно рассекречены и выложены на сайте АНБ.

Одноразовый шифроблокнот

Несколько лет назад одного британского айтишника надолго посадили за сотрудничество с террористами, с которыми он переписывался посредством самопального шифра, запрограммированного в Экселе. Несмотря на то, что ему вполне была доступна современная криптография, некомпетентность его подвела и легко вскрытая правоохранительными органами переписка была использована против него же в суде. Oops…

В криптографии есть несколько эмпирических законов, самый главный из которых формулируется очень просто: никогда не изобретайте собственный шифр! Шифры изобретают либо новички-дилетанты, либо специалисты по криптографии. В первом случае шифр легко ломается специалистом или даже просто более-менее соображающим дилетантом, во втором… бывает по-разному, особенно с учетом бурного роста производительности компьютеров. Но некоторые шифры выдерживают испытание временем. Об одном таком шифре и пойдет речь.

Для применения большинства современных надежных шифров требуется наличие более-менее приличной ЭВМ. Но, к счастью, есть шифр, который доступен в любые века и времена и не требует серьезных вычислительных мощностей, оставаясь принципиально невзламываемым. Более того, это единственный на сегодняшний день шифр, невзламываемость которого доказывается математически (это доказал Клод Шеннон в 1945 году). Знакомьтесь: шифр Вернама, или, как его еще называют в бумажном варианте, одноразовый шифроблокнот.

Но, прежде, чем речь пойдет о самом шифре, следует вспомнить историю криптографии. На эту тему очень рекомендую книгу «Взломщики кодов» Дэвида Кана, в ней хорошо показано как на протяжении многих столетий шифр и дешифровка всегда шли ноздря к ноздре, причем пресловутые «черные кабинеты» чаще всего опережали примитивную криптографию, а последствия зачастую имели серьезнейшие масштабы: достаточно вспомнить печально известную телеграмму Циммермана. И, несмотря на то, что тот же шифр Виженера в реальной истории взломали достаточно поздно, кто знает — не попадет ли ваша шифровка в руки какого-нибудь местного Блеза Паскаля и не торкнет ли его от простой идеи переписать сообщение колонкой шириной в предполагаемую длину ключа и анализировать колонки? А если от безопасности ваших сообщений зависит ваша жизнь, не лучше ли использовать то, что не взломает ни гений из прошлого, ни АНБ из настоящего, ни пришельцы из будущего? Ну, при дОлжном соблюдении технологии шифрования? А?

Кстати, о соблюдении технологии. В ней кроется и ахиллесова пята одноразового шифроблокнота. Нарушение правил ведет к тому, что абсолютно надежный шифр превращается в достаточно легко взламываемый. Пример тому — советская переписка, небольшой процент которой американцам удалось вскрыть благодаря тому, что в результате раздолбайства НКВД в сороковые годы часть случайных последовательностей использовалась неоднократно (см. проект VENONA). Как следствие, вскрытие шпионской сети Розенбергов, укравших для СССР секрет атомной бомбы.

Итак, как это работает. Для шифрования открытого текста используются шифрблокноты, на каждом листе которых написана последовательность случайных цифр. Как у отправителя, так и у получателя должны быть два заранее составленных одинаковых шифроблокнота.

Вначале надо превратить ваш текст в цифры. Для этого используется сжимающая таблица (straddling checkerboard). В каком-то смысле это аналог алгоритмов, лежащих в основе zip, rar и т.п., только таблица сжатия у нас фиксированная. Нет, вы конечно можете и просто сопоставить буквам цифры по принципу А=1, Б=2 и т.д, но из-за избыточности языка вы будете вынуждены потом шифровать где-то на треть больше. Просидев несколько часов с карандашом за тупой арифметикой, вы быстро оцените достоинства сжимающей таблицы…

Для создания сжимающей таблицы запоминаем: А И ТЕСНО. Тут задействовано семь самых часто встречающихся букв в русском языке. Для английского берем скажем AT ONE SIR (в английском языке меньше букв и можно обойтись только двумя доп. строками) и т.п. Составляем таблицу, в первой строке которой идут часто встречающиеся символы, а в остальных остатки алфавита. Обратите внимание, что в первой строке не задействованы цифры 8, 9 и 0, и они же обозначают, что буква (реже встречающаяся) кодируется не одной цифрой, а двумя. Итак, для кодирования буквы ищем ее, если она находится в первой строке, то мы выбираем номер ее колонки (например Т=3), если она в остальных колонках, то мы вначале выбираем номер ее строки, а потом номер колонки, например Б=81, а ?=07:

1 2 3 4 5 6 7 8 9 0 А И Т Е С Н О8 Б В Г Д Ж З К Л М П9 Р У Ф Х Ц Ч Ш Щ Ъ Ы0 Ь Э Ю Я . , ?

Можно добавить еще-что-то полезное в оставшиеся три ячейки в последней строке (в реальности кроме букв часто использовались специальные коды для начала передачи цифр, начала передачи специальных кодов из кодовых таблиц и т.п.). Итак, нам надо зашифровать короткое сообщение:

ПОБЕГ ЗАВТРА

Первая буква сообщения находится во второй строке таблицы, так что берем номер строки, а потом номер колонки: 80. Далее вторая буква имеет высокую частоту и находится в первой строке, поэтому берем только ее колонку: 7. Получаем последовательность цифр. Добиваем нулями последнюю группу до пяти цифр:

80781 48386 18239 11000

Цифры желательно записывать группами по пять. Так модно у связистов это нужно вам же самим, т.к. пять цифр проще всего удержать в памяти и ничего не перепутать. Это полезная практика, которой так же обучают радистов при работе с азбукой Морзе.

Но ПОКА ЧТО это еще не шифр! Закодированный вышеприведенным способом текст уже заметно сложнее взять в лоб простым частотным анализом, но все равно на шифр оно никак не тянет. Теперь выдираем страницу из одноразового шифроблокнота, приведенного на иллюстрации и начинаем с ней работать. Внимание! Никогда нельзя в шифровке указывать номер страницы шифроблокнота, чтобы не дать возможность проанализировать последовательность шифровок или угадать время ее отправки (что может оказаться не менее критичным, чем ее содержимое)! Вместо этого для идентификации страницы используется первая группа, ее не следует использовать для шифрования, а записать как есть. Под цифрами шифровки записываем цифры одноразового кода начиная со второй группы, после чего складываем цифры в каждой колонке, всегда отбрасывая возникающий перенос:

80781 48386 18239 11000+ 14358 89753 24133 40169 26799= 14358 69434 62419 58398 37799

Вот это уже и есть шифровка:

14358 69434 62419 58398 37799

Теперь осталось сжечь страницу, с помощью которой мы шифровали, и отправить нашу шифровку по назначению. Получатель достанет свою копию шифроблокнота, найдет нужную страницу по первой группе и произведет вначале обратную операцию, вычитая из каждой цифры шифровки цифру с шифроблокнота, всегда отбрасывая минус. Затем возьмет сжимающую таблицу и с помощью нее уже окончательно раскодирует текст. Точно так же — берем 8, ага, это вторая строка, 0 колонка, значит первая буква П., и так далее. А потом тоже сожжет свою копию и больше никто и никогда не сможет расшифровать перехваченное сообщение. А если шифроблокнот будет вовремя уничтожен, то и терморектальный криптоанализ не поможет в расшифровке: ни один человек не в состоянии вспомнить хотя бы полстраницы шифроблокнота со случайными числами.

Ну, а теперь самое главное (и самое трудоемкое): как сгенерировать достаточное количество случайных чисел. Ведь одноразовый шифроблокнот предполагает уничтожение каждой страницы после расшифровки, и для передачи определенного объема текста надо такое же количество случайных данных! Это и является вторым недостатком одноразового шифроблокнота: создание шифроблокнотов занятие длительное и трудоемкое, причем надо суметь создать реально случайную последовательность. Первое, что приходит в голову, это взять кости и накидать набор чисел, вот только на обычных игральных костях всего лишь цифры от 1 до шести, а кидать пару костей и складывать цифры нельзя, т.к. распределение суммы уже подчиняется вполне понятной закономерности и у вас выйдет не совсем случайная последовательность цифр. Можно конечно попробовать сделать кость на d10, как на иллюстрации справа, но попробуйте ее выточить напильником с достаточной точностью!

Если же использовать обычные игральные кости, то надо составить таблицу и уже использовать ее для генерации случайных чисел, кидая кость для каждого числа два раза, игнорируя последовательности, начинающиеся с шестерки:

11 = 0 21 = 6 31 = 2 41 = 8 51 = 4 12 = 1 22 = 7 32 = 3 42 = 9 52 = 5 13 = 2 23 = 8 33 = 4 43 = 0 53 = 6 14 = 3 24 = 9 34 = 5 44 = 1 54 = 7 15 = 4 25 = 0 35 = 6 45 = 2 55 = 8 16 = 5 26 = 1 36 = 7 46 = 3 56 = 9

Так же можно использовать шары лото, пронумерованные от 0 до 9. При этом, достав шар и записав его номер, его необходимо положить обратно и перемешать всю кучу, иначе опять же возникнут проблемы с распределением.

Процесс генерации случайных чисел вручную дьявольски трудоемкий, а с учетом того, что в военное время объемы шифрованной переписки вырастает в порядки, понятно, что одноразовый шифроблокнот может быть использован только для передачи самой важной информации.

Но! Вооружившись всего лишь карандашом, бумагой и игральной костью можно будет потом, после создания пары шифроблокнотов и передачи одного из них по безопасному каналу, переписываться через всю галактику. При этом вы будете уверены, что ваше сообщение никто не прочтет, кроме владельца второй копии шифроблокнота. Разве что где-то какой-нибудь джедай использует Силу, дабы прочитать прошлое и увидеть вас записывающим получившуюся случайную последовательность…

Криптоанализ «Энигмы»

Криптография*

All specialists unanimously agreed that a reading [of the Enigma] is impossible.
Admiral Kurt Fricke, Chief of Naval War Command

Энигма — роторная шифровальная машина, использовавшаяся нацистской Германией в годы Второй мировой войны. Благодаря влиянию, оказанному на ход войны, взлом Энигмы стал, возможно, самым ярким моментом в многовековой истории криптоанализа. В этом топике я бы хотел рассказать о методе взлома, использовавшимся в Блетчли-парк, а так же описать устройство самой машины.

Роторные машины

Впервые шифровальные роторные машины начали использоваться в начале 20 века. Основным компонентом таких устройств является диск (он же ротор) с 26 электрическими контактами на обоих сторонах диска. Каждый контакт соответствовал букве английского алфавита. Соединение контактов левой и правой сторон реализовывало шифр простой замены. При вращении диска контакты смещались, изменяя тем самым подстановку для каждой буквы. Один диск обеспечивал 26 различных подстановок. Это означает, что при шифровании одного и того же символа, получаемая в результате последовательность начинает повторяться через 26 шагов.
Для увеличения периода последовательности можно использовать несколько роторов, соединенных последовательно. При совершении полного оборота одного из дисков, следующий диск сдвигается на одну позицию. Это увеличивает длину последовательности до 26ⁿ, где n — количество соединенных последовательно роторов.
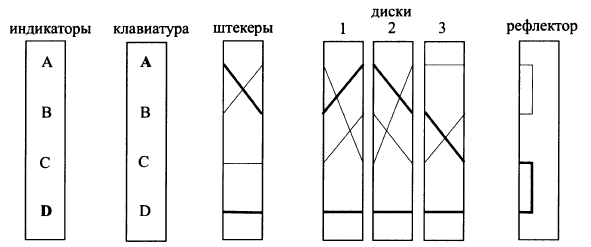
В качестве примера рассмотрим следующее изображение упрощенной роторной машины:

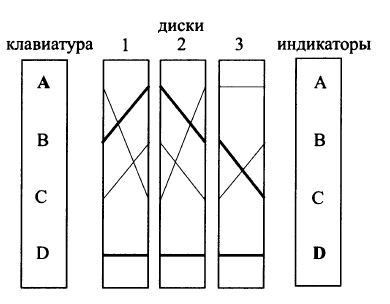
Приведенная машина состоит из клавиатуры (для ввода символа), трех дисков, индикатора (для отображения криптотекста) и реализует шифрование 4 символов: A, B, C, D. В начальной позиции первый диск реализует подстановку: A-C; B-A; C-B; D-D. Подстановки второго и третьего дисков равны A-B; B-C; C-A; D-D и A-A; B-C; C-B; D-D соответственно.
При нажатии буквы B на клавиатуре замыкается электрическая цепь, зависящая от текущего положения роторов, и на индикаторе загорается лампочка. В приведенном выше примере буква B будет зашифрована в C. После чего первый ротор сдвинется на одну позицию и настройки машины приобретут следующий вид:

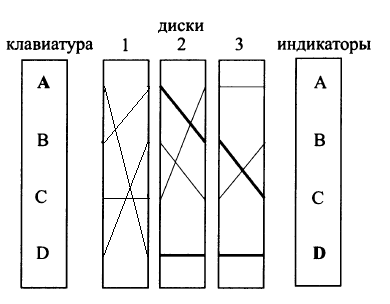
Энигма

Энигма является наиболее популярным представителем мира шифровальных роторных машин. Она использовалась германскими войсками во время второй мировой войны и считалась практически не взламываемой.
Процедура шифрования Энигмы реализована как в приведенном выше примере за исключением некоторых дополнительных штрихов.
Во-первых, число роторов в разных версиях Энигмы могло отличаться. Наиболее распространенной была Энигма с тремя роторами, но использовался так же вариант с четырьмя дисками.
Во-вторых, процесс расшифровки демонстрационной роторной машины, описанной выше, отличается от процесса шифрования. Каждый раз для расшифровки придется менять левый и правый ротор местами, что может быть не совсем удобным. Для решения этой проблемы в Энигме был добавлен еще один диск, который назывался рефлектор. В рефлекторе все контакты были соединены попарно, реализуя тем самым повторное прохождение сигнала через роторы, но уже по другому маршруту. В отличие от остальных роторов рефлектор всегда находился в фиксированном положении и не вращался.

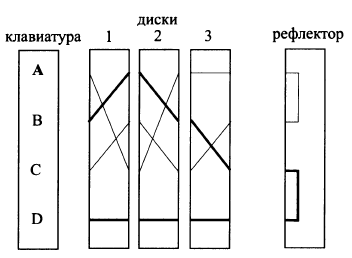
Добавим рефлектор, реализующий замену (A-B; C-D) к нашей демонстрационной шифровальной машине. При нажатии на клавишу B сигнал проходит через роторы и поступает в рефлектор через контакт C. Здесь сигнал «отражается» и возвращается обратно, проходя через роторы в обратном порядке и по другому пути. В результате чего буква B на выходе преобразуется в D.
Обратите внимание, что если нажать клавишу D, то сигнал пойдет по той же самой цепи, преобразовывая D в B. Таким образом наличие рефлектора делало процессы шифрования и дешифрования идентичными.
Еще одно свойство Энигмы, связанное с рефлектором, заключается в невозможности шифрования какой-либо буквы в саму себя. Это свойство сыграло очень важную роль при взломе Энигмы.

Получившееся устройство уже очень похоже на настоящую Энигму. С одной незначительной оговоркой. Стойкость подобной машины упирается в секретность внутренней коммутации роторов. Если устройство роторов будет раскрыто, то взлом сводится к подбору их начальных позиций.
Так как каждый ротор может находится в одной из 26 позиций, для трех роторов получаем 26³=17476 вариантов. При этом сами роторы тоже могут располагаться в произвольном порядке, что увеличивает сложность в 3! раз. Т.е. пространство ключей такой машины составит 6*17576=105456. Этого явно не достаточно для того, чтобы обеспечить высокий уровень безопасности. Поэтому Энигма было оснащена еще одним дополнительным инструментом: коммутационной панелью. Соединяя на коммутационной панели буквы попарно можно было добавить еще один дополнительный шаг к шифрованию.

К примеру, предположим что на коммутационной панели буква B соединена с буквой A. Теперь при нажатии на A сперва происходит подстановка A-B, и на вход первого ротора подается буква B.
Аналогичным образом происходит расшифровка сообщения. При нажатии клавиши D роторы и рефлектор производят преобразование D-D-D-D-C-B-A-B. После чего коммутационная панель преобразует B в A.

Анализ стойкости Энигмы

Реальная Энигма отличалась от описанной демонстрационной машиной только в одном. А именно в устройстве роторов. В нашем примере ротор изменяет свое положение только при совершении полного оборота предыдущим диском. В настоящей Энигме каждый диск имел специальную выемку, которая в определенной позиции подцепляла следующий ротор и сдвигала его на одну позицию.
Расположение выемки для каждого из роторов можно было регулировать с помощью специальных внешних колец. Начальное положение колец не влияло на коммутацию роторов и на результат шифрования отдельно взятой буквы, поэтому кольца не учитываются при расчете пространства ключей Энигмы.
Итак, базовая модель Энигмы имела 3 различных ротора, пронумерованных римскими цифрами I, II, III и реализующих следующие подстановки:
Entry = ABCDEFGHIJKLMNOPQRSTUVWXYZ
I = EKMFLGDQVZNTOWYHXUSPAIBRCJ
II = AJDKSIRUXBLHWTMCQGZNPYFVOE
III = BDFHJLCPRTXVZNYEIWGAKMUSQO
При шифровании роторы можно было располагать в любой последовательности, что для трех роторов дает 6 разных комбинаций.
Помимо этого каждый ротор мог быть установлен в одной из 26 возможных стартовых позиций. Т.е. начальное положение роторов имеет всего
6*26³=105456 комбинаций.
Количество всех возможных соединений на коммутационной панели вычисляется по формуле n! /((n-2m)! m! 2^m), где n — количество букв алфавита, m — количество соединенных пар.
Для 26 буква английского алфавита и 10 пар это составляет 150738274937250=2⁴⁷ различных комбинаций.
Таким образом базовая версия Энигмы с тремя роторами имела солидное даже по современным меркам пространство ключей:
150738274937250*105456=15,896,255,521,782,636,000≈2⁶⁴.
Такое огромное число вариантов внушало обманчивое чувство неуязвимости.

Криптоанализ Энигмы

Большое пространство ключей обеспечивает шифру Энигмы достаточно серьезный уровень стойкости к атакам по известному шифртексту.
Полный перебор 2⁶⁴ вариантов даже на современных компьютерах дело не простое.
Однако все меняется если применить атаку с известным открытым текстом. Для такого случая существует весьма хитроумный метод, позволяющих пренебречь настройками коммутационной панели в процессе поиска ключевой комбинации, что сводит пространство ключей Энигмы всего к 105456 комбинациям и делает весь шифр фатально уязвимым.

Метод эксплуатирует наличие в паре открытый-закрытый текст так называемых «циклов». Чтобы объяснить понятие «цикл», рассмотрим следующее открытое сообщение P и соответствующий ему криптотекст C, зашифрованный Энигмой.

P = WETTERVORHERSAGEBISKAYA
C = RWIVTYRESXBFOGKUHQBAISE

Запишем каждый символ из пары в виде таблицы:

w

e

t

t

e

r

v

o

r

h

e

r

s

a

g

e

b

i

s

k

a

y

a

r

w

i

v

t

y

r

e

s

x

b

f

o

g

k

u

h

q

b

a

i

s

e

Обратите внимание на подстановки, реализуемые энигмой в 14, 15 и 20 позициях. На 14 шаге буква A шифруется в G. Последняя, в свою очередь, шифруется в K на 15 шаге. И затем буква K зашифровывается в A на 20 шаге, закольцовывая тем самым цепочку A-G-K-A. Такие закольцованные цепочки называются циклами. Наличие циклов позволяет разделить задачу взлома Энигмы на две простые составные части: 1) поиск стартового положения роторов и 2) поиск соединений коммутационной панели при известных установках роторов.

Мы знаем, что при шифровании в Энигме происходит несколько преобразований. Сперва сигнал проходит через коммутационную панель. Результат преобразования на коммутационной панели поступает в роторы. После чего сигнал попадает на рефлектор и возвращается через роторы на коммутационную панель, где выполняется последняя подстановка. Все эти операции можно представить математической формулой:
E_i = S^-1R^-1TRS, где
S и S^-1, — преобразование на коммутационной панели на входе и выходе соответственно;
R и R^-1 — преобразование в роторах на входе и выходе;
T — преобразование на рефлекторе.
Опустив коммутационную панель выразим внутреннее преобразование Энигмы через P_i:
P_i = R^-1TR
Теперь шифрование можно записать как:
E_i = S^-1P_iS

Используя формулу перепишем подстановки из примера в 14, 15 и 20 позициях.
S^-1P₁₄S(A) = G или что одно и тоже P₁₄S(A) = S(G).
P₁₅S(G) = S(K)
P₂₀S(K) = S(A)
Заменив в последнем выражении S(K) получим:
P₂₀P₁₅P₁₄S(A) = S(A) (1), где S(A) — буква, соединенная с A на коммутационной панели.
Теперь атака сводится к тривиальному перебору всех возможных установок ротора. Для каждой комбинации роторов необходимо проверить выполнение равенства (1). Если равенство выполняется для буквы S, это означает что найдена правильная конфигурация роторов и что буква A соединена на коммутационной панели с буквой S. Поиск остальных пар сводится к по буквенной расшифровке криптотекста и сопоставлению результата с известным открытым текстом.
Следует отметить, что с вероятностью 1/26 равенство может выполняться и при неправильной установке роторов, поэтому для повышения надежности алгоритма желательно использовать несколько «циклов».
Еще один важный момент связан с тем, что атакующему может быть известна только часть зашифрованного сообщения. И в таком случае, прежде всего ему потребуется найти местоположение известного текста в полученной криптограмме. В решении этой задачи очень сильно помогает знание того факта, что Энигма никогда не шифрует букву саму в себя. Т.е. для нахождения правильного смещения нужно найти такую позицию в криптотексте при которой ни одна из букв закрытого текста не дублируется буквой открытого сообщения.

P.S.