Пример 2. 1. Нулевой шаг детализации

1. Нулевой шаг детализации

2. Первый шаг детализации

Как вы нашли наименьшее число? Вы просмотрели всю последовательность, рассматривая каждое число и проверяя, не наименьшее ли оно. Это повторяющееся действие — значит, должен быть цикл. Какой? Так как количество повторений известно, то может быть применен цикл с параметром, в N – S-диаграммах являющийся, как указывалось выше, циклом с предусловием:

3. Второй шаг детализации

Так что же делать, чтобы понять, какое наименьшее? Детализируем внутренний блок на последней диаграмме. Вот что мы делаем, сравнивая каждое число с наименьшим, найденным до сих пор: если следующее число меньше, оно становится наименьшим, в противном случае старое остается наименьшим3.

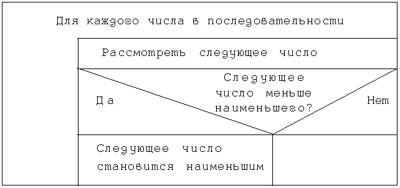
4. Третий шаг детализации

Но как вы получили первое наименьшее число? Простейший способ сделать это — принять за наименьшее число первое число в последовательности чисел:

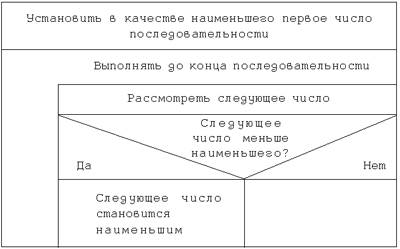
Проверим работу этого алгоритма на примере последовательности чисел: 51 25 35 79 13 26.

1. Установить в качестве наименьшего первое число последовательности (51).

2. Конец последовательности? — Нет.

3. Следующее число — 25.

4. 25 < 51? — Да.

5. Устанавливаем в качестве наименьшего число 25.

6. Конец последовательности? — Нет.

7. Следующее число — 35.

8. 35 < 25? — Нет.

9. Конец последовательности? — Нет.

10. Следующее число — 79.

11. 79 < 25? — Нет.

12. Конец последовательности? — Нет.

13. Следующее число — 13.

14. 13 < 25? — Да.

15. Устанавливаем в качестве наименьшего число 13.

16. Конец последовательности? — Нет.

17. Следующее число — 26.

18. 26 < 13? — Нет.

19. Конец последовательности? Да.

Таким образом, наименьшее число в последовательности равно 13.

Ссылки

1. http://ru.wikipedia.org/wiki/%C4%E8%E0%E3%F0%E0%EC%EC%E0_%CD%E0%F1%F1%E8_%97_%D8%ED%E5%E9%E4%E5%F0%EC%E0%ED%E0

2. http://inf.1september.ru/2006/03/12.htm

3. http://skyfly.on.ufanet.ru/tp/56.html

4. http://www.nesterova.ru/bibl/algorithm_lang/Kniga/Kniga/Parts1/Parts1/index.htm

5. http://trprog.ru/flowformi.html

6. http://trprog.ru/diagrammi-nassishneydermana.html

7. http://www.interface.ru/case/defs4.htm

Варианты заданий

Разработать Flow-диаграммы и диаграммы Насси – Шнейдермана для алгоритмов решения следующих задач.

1. Определить, является ли число А делителем числа В.

2. Даны три целых числа. Определить, сколько из них четных.

Примечание. Циклы не использовать.

3. В чемпионате по футболу команде за выигрыш дается 3 очка, за проигрыш — 0, за ничью — 1. Известно количество очков, полученных командой за игру. Определить словесный результат игры (выигрыш, проигрыш или ничья).

Примечание. Три блока ветвления не использовать.

4. Мастям игральных карт условно присвоены следующие порядковые номера: масти “пики” — 1, масти “трефы” — 2, масти “бубны” — 3, масти “червы” — 4. По заданному номеру масти m (1 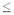m 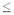4) определить название соответствующей масти.

Примечание. Блоки ветвления не использовать.

5. Найти сумму 10 заданных целых чисел.

6. Даны n целых чисел. Определить, сколько из них четных.

7. Известен рост каждого из 20 учеников класса. Рост мальчиков условно задан отрицательными числами. Определить средний рост мальчиков и средний рост девочек.

8. Дано целое число. Если оно положительное, то вычислить средний рост девочек (см. задачу 7), в противном случае вычислить средний рост мальчиков.

9. В задаче 7 выяснить, верно ли, что средний рост мальчиков превышает средний рост девочек более чем на 10 см.

10. Дано натуральное k. Вывести k-ую цифру последовательности 1123581321…, в которой выписаны подряд все числа Фибоначчи.

11. Дана последовательность из не менее чем 2-х натуральных чисел, за которой следует 0. Вычислить сумму тех из них, порядковые номера которых простые числа.

12. Дано натуральное k. Вывести k-ую цифру последовательности 149162536…, в которой выписаны подряд квадраты всех натуральных чисел.

13. Дана непустая последовательность из натуральных чисел, за которой следует 0. Вычислить сумму тех из них, порядковые номера которых числа Фибоначчи.

14. Вывести все простые делители заданного натурального числа.

15. Дано целое n>2. Вывести все простые числа из диапазона [2,n].

16. Дано 10 натуральных чисел. Найти их наибольший общий делитель.

17. Определить, является ли заданное натуральное число совершенным, т.е. равно ли это число сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).

18. Дана непустая последовательность ненулевых чисел, за которой следует 0. Определить, сколько раз в этой последовательности меняется знак (напр., в последовательности 1, -34, 8, 14, -5 знак меняется 3 раза).

19. Дано не менее 3-х различных натуральных чисел, за которыми следует 0. Определить 3 наибольших числа в последовательности.

20. Вывести в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр (операции деления не использовать).

21. Дана последовательность из 20 целых чисел. Определить количество чисел в наиболее длинной подпоследовательности из подряд идущих нулей (например, для последовательности 250070008055 ответ 3).

22. Дано натуральное k. Вывести k-ую цифру последовательности 12345678910111213…, в которой выписаны подряд все натуральные числа.

23. Даны натуральные числа k и n. Вычислить сумму чисел между k-ым и n-ым элементами последовательности степеней числа 3: 1392781…, но сами граничные элементы в сумму не включать.

24. Логической переменной t присвоить значение true или false, в зависимости от того, можно или нет натуральное число n представить в виде суммы трех полных квадратов.

25. Логической переменной p присвоить значение true, если целое n
(n > 1) – простое число, и значение false иначе.

26. Дана непустая последовательность слов из строчных русских букв; между соседними словами - запятая, за последним словом - точка. Напечатать в алфавитном порядке все глухие согласные буквы, которые входят в текст.