Вероятность попадания в заданный интервал нормальной случайной величины

Дисперсия нормальной случайной величины.

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.

Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.

Расчетные формулы:

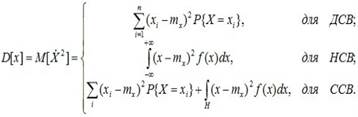(6.9)

Дисперсия может быть вычислена через второй начальный момент:

(6.10)

Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.

Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ.

Средним квадратическим отклонением (СКО) СВ X называется характеристика

. (6.11)

СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ.

Свойства дисперсии

Дисперсия постоянной величины с равна нулю.

Доказательство: по определению дисперсии

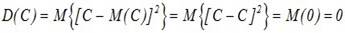
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.

D[X+c] = D[X].

Доказательство: по определению дисперсии

(6.12)

3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с².

Доказательство: по определению дисперсии

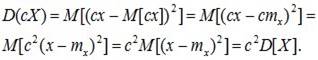. (6.13)

Для среднего квадратичного отклонения это свойство имеет вид:

(6.14)

Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е. 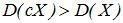. Если 0<½с½<1, то .

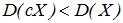Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:

[ m - 3s; m + 3s; ].(6.15)

Вероятность попадания в заданный интервал нормальной случайной величины

Как уже было установлено, вероятность того, что непрерывная случайная величина 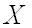примет значение, принадлежащее интервалу 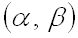, равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
.
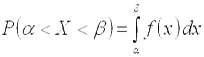Для нормально распределенной случайной величины соответственно получим:
.
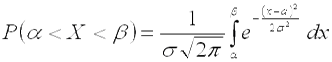Преобразуем последнее выражение, введя новую переменную 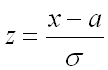. Следовательно, показатель степени выражения, стоящего под интегралом преобразуется в:
.
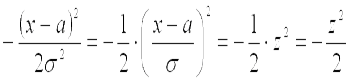Для замены переменной в определенном интеграле еще необходимо заменить дифференциал и пределы интегрирования, предварительно выразив переменную из формулы замены:
;
;
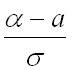– нижний предел интегрирования;
– верхний предел интегрирования;
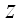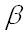(для нахождения пределов интегрирования по новой переменной в формулу замены переменной были подставлены и – пределы интегрирования по старой переменной ).
Подставим все в последнюю из формул для нахождения вероятности:

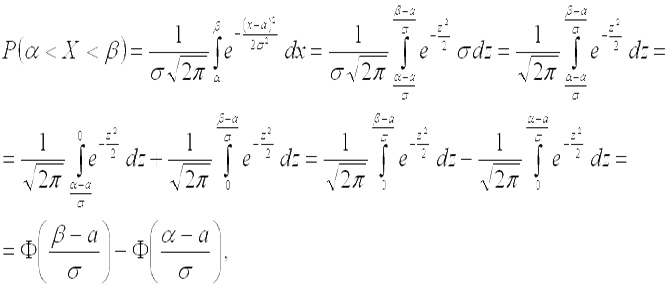
где – функция Лапласа.
Вывод: вероятность того, что нормально распределенная случайная величина 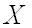примет значение, принадлежащее интервалу 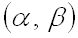, равна:
,
где 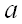– математическое ожидание, 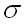– среднее квадратическое отклонение данной случайной величины.

23. Распределения «хи-квадрат», Стьюдента и Фишера

С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. В дальнейших разделах книги много раз встречаются эти распределения.

Распределение Пирсона 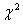(хи - квадрат) – распределение случайной величины

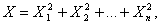
где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных [8, 9, 11, 16].

Распределение t Стьюдента – это распределение случайной величины

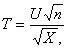
где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

Распределение Стьюдента было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов.

В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д. [8, 9, 11, 16].

Распределение Фишера – это распределение случайной величины

где случайные величины Х₁ и Х₂ независимы и имеют распределения хи – квадрат с числом степеней свободы k₁ и k₂ соответственно. При этом пара (k₁, k₂) – пара «чисел степеней свободы» распределения Фишера, а именно, k₁ – число степеней свободы числителя, а k₂– число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.

Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики [8, 9, 11, 16].

Выражения для функций распределения хи - квадрат, Стьюдента и Фишера, их плотностей и характеристик, а также таблицы, необходимые для их практического использования, можно найти в специальной литературе (см., например, [8]).