Смешанное произведение векторов
Смешанным произведением трех векторов 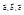 называется число, получаемое следующим образом: векторное произведение
называется число, получаемое следующим образом: векторное произведение 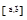 умножается скалярно на вектор
умножается скалярно на вектор 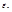 Смешанное произведение векторов
Смешанное произведение векторов 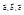 обозначается
обозначается 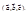 Таким образом,
Таким образом,  Если векторы
Если векторы 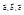 заданы своими координатами в ортонормированном базисе, то
заданы своими координатами в ортонормированном базисе, то
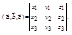
Объем параллелепипеда V, построенного на векторах 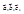 можно вычислить по формуле
можно вычислить по формуле 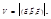 Для того чтобы три вектора
Для того чтобы три вектора 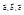 были компланарны, необходимо и достаточно, чтобы
были компланарны, необходимо и достаточно, чтобы 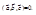
Прямая на плоскости.
В декартовой прямоугольной системе координат Оxy прямая на плоскости может быть задана уравнениями:
– общее уравнение прямой
Ax + By + C = 0; (4.3)
– уравнение прямой, проходящей через точку M0(x0, y0)перпендикулярно нормальному вектору 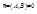 :
:
A(x – x0) + B(y – y0) = 0;
– уравнение прямой, проходящей через точку M0(x0, y0)параллельно направляющему вектору 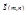 (каноническое уравнение прямой):
(каноническое уравнение прямой):
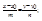
– параметрические уравнения прямой
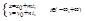 ;
;
– уравнение прямой в отрезках
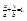
Здесь a и b – величины отрезков, отсекаемых на осях координат Ox и Oy (т.е. длины, взятые с соответствующими знаками);
– уравнение прямой, проходящей через две данные точки M1(x1, y1) и M2(x2, y2):
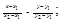
– уравнение прямой с угловым коэффициентом k, проходящей через точку M0(x0, y0):
y – y0 = k(x – x0).
Расстояние 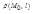 от точки M0(x0, y0) до прямой l, заданной уравнением (4.3), определяется по формуле
от точки M0(x0, y0) до прямой l, заданной уравнением (4.3), определяется по формуле
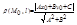 . (4.4)
. (4.4)
Две прямые, заданные уравнениями A1x + B1y + C1 = 0и
A2x + B2y + C2 = 0, параллельны, если 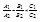 , и перпендикулярны, если A1A2 + B1B2 = 0.
, и перпендикулярны, если A1A2 + B1B2 = 0.
Плоскость.
Плоскость в прямоугольной системе координат может быть задана уравнениями:
Ax + By + Cz + D = 0 – общее уравнение плоскости. (4.5)
Если в уравнении (4.5) отсутствует свободный член D, то плоскость проходит через начало координат; если в уравнении (4.5) отсутствует одна из переменных, то плоскость параллельна той оси, название которой не входит в это уравнение;
A(x – x0) + B(y – y0) + C(z – z0) = 0 –
уравнение плоскости, проходящей через точку М0(x0, y0, z0) перпендикулярно нормальному вектору 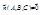 ;
; 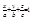 – уравнение плоскости в отрезках,
– уравнение плоскости в отрезках,
где а, b, c – величина отрезков, отсекаемых плоскостью на координатных осях;
– уравнение плоскости, проходящей через три данные точки M1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3):
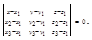 (4.6)
(4.6)
Величина угла φмежду двумя плоскостями A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z +D2 = 0 вычисляется по формуле
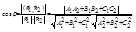
Условие перпендикулярности данных плоскостей запишется в виде
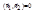 или
или 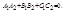
Условие параллельности рассматриваемых плоскостей имеет вид
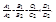
Расстояние 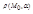 от точки M0(x0, y0, z0) до плоскости
от точки M0(x0, y0, z0) до плоскости 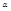 , заданной уравнением (4.5), вычисляется по формуле
, заданной уравнением (4.5), вычисляется по формуле
Линии второго порядка
Линией второго порядка называется множество точек плоскости, координаты x, y которых в прямоугольной системе координат удовлетворяют уравнению второй степени
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0. (4.7)
Уравнение (4.7) называется общим уравнением линии второго порядка (А, В, С не равны нулю одновременно).
При помощи преобразования прямоугольной системы координат (параллельного переноса и поворота) всегда можно найти такую новую прямоугольную систему координат, в которой уравнение (4.7) имеет один из следующих трех видов (каноническое уравнение):
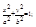 (4.8)
(4.8)
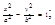 (4.9)
(4.9)
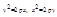 , (4.10)
, (4.10)
где a, b, p – положительные числа. Уравнение (4.7) может определять так называемую вырожденную кривую (пустое множество, точ-ку, прямую, пару прямых). При этом линия, приводимая к виду (4.8), (4.9), (4.10), называется соответственно эллипсом, гиперболой или параболой.
Эллипс с каноническим уравнением 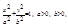
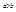 , имеет форму, изображенную на рис. 4.4.
, имеет форму, изображенную на рис. 4.4.
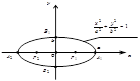
Рис. 4.4
Точки F2(–с, 0) и F1(с, 0), где 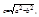 называются фокусами эллипса.
называются фокусами эллипса.
Числа а и b называются полуосями эллипса.
Гипербола с каноническим уравнением 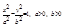 имеет форму, изображенную на рис. 4.5.
имеет форму, изображенную на рис. 4.5.
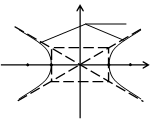
Рис. 4.5
Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках А1(а,0), А2(–а, 0), называемых вершинами гиперболы. Числа a и b – полуоси гиперболы: а – действительная полуось, b – мнимая. Точки F2(–c, 0) и F1(c, 0), где 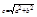 , называются фокусами гиперболы.
, называются фокусами гиперболы.
Парабола с каноническим уравнением 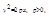 имеет форму, изображенную на рис. 4.6.
имеет форму, изображенную на рис. 4.6.

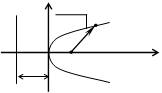
Рис. 4.6
Число p называется параметром параболы, точка О – ее вершиной, а ось Оx – осью параболы, вектор 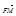 – фокальный радиус-вектор точки М. Прямая
– фокальный радиус-вектор точки М. Прямая 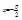 называется директрисой параболы.
называется директрисой параболы.
