Двойное лучепреломление

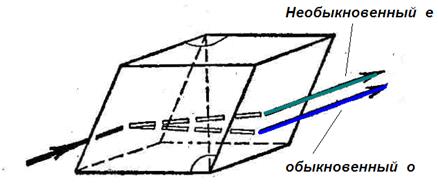
Рис.8-4

5. При прохождении света через все прозрачные кристаллы, за исключением кубических, наблюдается явление, получившее название двойного лучепреломления(рис.8-4). Это явление заключается в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющие­ся, с разными скоростями и в различных направле­ниях.

У одноосных крис­таллов:

А). один из преломленных лучей подчиняется обычному закону преломления, в частности он лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Этот луч назы­вается обыкновенным.

Б). Другой луч называется необыкновенным (его обозначают бук­вой е). Для этого луча закон преломления не выполняется. Даже при нормальном падении света на кристалл необыкновенный луч отклоняется от нормали. Кроме того, необыкновенный луч не лежит, как правило, в одной пло­скости с падающим лучом и нормалью к преломляющей поверхности.

В). Опыт показы­вает, что оба луча полностью поляризованы во взаимно перпенди­кулярных направлениях.

6. Плоскость колебаний обыкновенного луча перпендикулярна к главному сечению кристал­ла(на рисунке эти колебания изображены точками).

В необыкновенном луче колебания светового вектора совер­шаются в плоскости, совпадающей с главным сечением(стрелки)

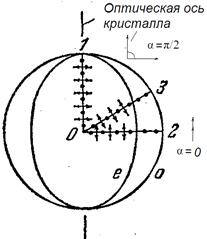
Рис.8-5

Представим, что в точке 0 внутри кристалла (рис.8-5) помещается точечный источник света. Если изобразить скорость обыкновенного луча в виде отрезков, отложенных по разным направ­лениям, то получится сферическая поверхность.

На рисунке пока­зано пересечение этой поверхности с плоскостью чертежа. Такая картина, как на рисунке, наблюдается в любом главном сечении, т. е. в любой плоскости, проходящей через оптическую ось. Поэтому обыкновенном луче при любом направлении (на рисунке указаны три направления: 1, 2 и3) вектор Е образует с оптической осью кристалла прямой угол, и скорость световой вол­ны будет одна и та же, равная.

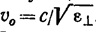
7. Так как колебания в необыкновенном луче совершаются в главном сече­нии, тодля разных лучей направления колебаний векто­ра Е образуют с оптической осью разные углы α. Для луча 1 угол α равен π/2, вследствие чего скорость имеет значение 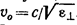, для луча 2 угол α =0 и скорость равна 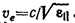. Для луча 3 скорость имеет промежуточное значение.

Можно показать, что волновая поверхность необыкновенных лучей представляет собой эллипсоид вращения. В местах пересечения с оптической осью кристалла этот эллипсоид и сфера, построенная для обыкновенных лу­чей, соприкасаются.

8. Одноосные кристаллы характеризуют показателем пре­ломления обыкновенного луча, равным

n₀=c/υ₀,

и показателем преломления необыкновенного луча, перпендикуляр­ного к оптической оси, равным

n_e=c/υ_e.

В зависимости от того, какая из скоростей, υ_e или υ₀, больше, различают положительные и отрицательные од­ноосные кристаллы.

У положительныхкристаллов υ_e<υ₀ (это означает, что п_е>п₀).

У отрицательных кристаллов υ_e>υ₀ (п_е<п_о).

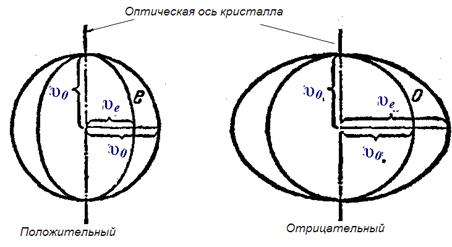
Рис.8-6

Построения Гюйгенса

позволяют определить ход обыкновенного и необыкновенного лучей в кристалле.

На рисунке 8-7 построены волновые поверхности обыкновенного и необыкновенного лучей с центром в точке 2, лежащей на поверхности кристалла. Построение выполнено для момента времени, когда волновой фронт падающей волны достигает точки 1. Огибающие всех вторичных волн для обыкновенно­го и необыкновенного лу­чей, очевидно, представля­ют собой плоскости (волны, центры которых лежат в промежутке между точка­ми 1 и 2, на рисунке не по­казаны)

Пре­ломленный луч о или е, выходящий из точки 2, про­ходит через точку касания огибающей с соответствую­щим волновым фронтом.

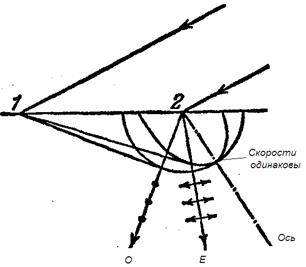
Рис.8-7

Три случая нормального падения света на поверхность кристалла, отличающиеся направлени­ем оптической оси: