П.4. Смешанное произведение векторов

Определение. Смешанным произведением упорядоченной тройки векторов 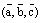называется скалярное произведение первого вектора навекторное произведение второго вектора на третий и обозначается

.

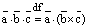Теорема. (Геометрический смысл смешанного произведения.)

1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах:

.

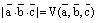2) 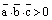, если тройка 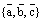– правоориентированная и 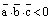в противном случае.

Доказательство. 1) Обозначим через 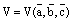объем параллелепипеда, построенного на данных векторах, как на его ребрах.

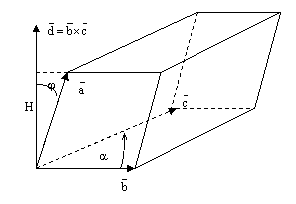
рис.3.

Объем параллелепипеда V равен произведению площади основания S на высоту Н: .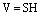

Площадь основания S численно равна модулю векторногопроизведения: 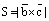, а высота Н равна модулю проекции вектора 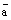на вектор :

.

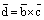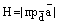Отсюда получаем:

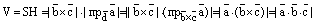, ч.т.д.

2) Так как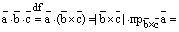

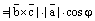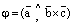, где , то знак смешанного произведениязависит от угла 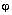. Если он острый, то смешанное произведение 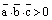и 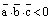, если угол 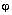– тупой. А это зависит, в свою очередь, от ориентации тройки векторов 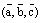. На рисунке 3 изображена правая тройка векторов 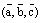. Если смотреть со стороны третьего вектора 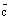, то кратчайший поворот первого вектора 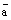ко второму 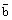осуществляется против часовой стрелки. В этом случае угол 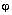– острый и 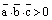. Если же тройка 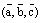– левая, то конец вектора 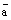будет лежать нижеплоскости векторов 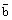и 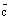(по сравнению с рис.3) и угол 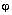будет тупым и 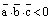, ч.т.д.

Теорема доказана.

Будем говорить, что тройки векторов 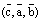и 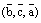получились из тройки 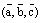с помощью круговой перестановки векторов. В первом случае третий вектор 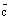переставляется на первое место, а векторы 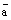и 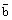сдвигаются вправо на второе и третье места соответственно. Во втором случае, первый вектор 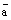переставляется на третье место, авекторы 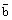и 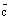сдвигаются влево на первое и второе места соответственно. Заметим, что при круговой перестановке векторов ни один из них не остается на своем месте.

Если же в тройке векторов меняются местами только два вектора, а один из векторов остается на своем месте, то такую перестановку мы будем называть не круговой перестановкой (или транспозицией). Так тройки 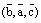, , 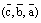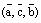получаются из тройки 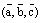транспозицией векторов. Так, например, в тройке 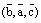остался на третьем месте вектор .

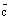Любую тройку векторов можно упорядочить 6-ю способами. Из них три тройки будут правыми и три тройки будут левыми.

Если тройка 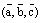правая (как на рис.3), то правыми будут и тройки полученные из нее круговой перестановко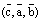й: и 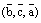. В то же время, тройка 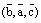будет левой и левой же будут тройки, полученные из нее круговой перестановко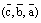й: и .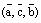

Лемма. Круговая перестановка в тройке векторов не изменяет ее ориентации, а транспозиция векторов изменяет ориентацию тройки на противоположную.

Доказательство проведите самостоятельно с использованием соответствующих картинок.

1) ;

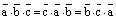2) ;

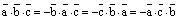3) .

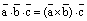Доказательство. 1) По модулю все эти смешанные произведения равны друг другу, т.к. параллелепипед, построенный на данных трех векторах, как его ребрах, не зависит от того, в каком порядке мы записываем его ребра и, соответственно, не изменяется его объем.

2) Знак смешанного произведения упорядоченной тройки векторов зависит от ее ориентации, которая не меняется при круговой перестановке и меняется при транспозиции, откуда и следуют доказываемые равенства.

3) Воспользуемся уже доказанным равенством, определением смешанного произведения и свойством коммутативности скалярногопроизведения:

.
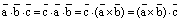