Передача параметров в функции по значению и по ссылке

Список параметров, передаваемый в функции, как было показано ранее, состоит из имен параметров и указаний их типов. Например, в заголовке

double FSum(double x1, double x2, int A)

указано три параметра x1, x2, A и определены их типы. Вызов такой функции может иметь вид:

double F = FSum(Y, x2, 5);

Это только один из способов передачи параметров в функцию, называемый передачей по значению. Работает он так. В момент вызова функции в памяти создаются временные переменные с именами x1, x2, A, и в них копируются значения аргументов Y, x2 и константы 5. на этом связь между аргументами и переменными x1, x2, A разрывается. Можно изменять внутри функции значения x1, x2, A, но это никак не отразится на значениях аргументов.

Возможен и другой способ передачи параметров – вызов по ссылке. В этом случае оператор вызова дает вызываемой функции возможность прямого доступа к передаваемым данным, а также возможность изменения этих данных. Чтобы показать, что параметр функции передан по ссылке, после типа параметра в прототипе функции ставится символ амперсанта (&); такое же обозначение используется в списке типов параметров в заголовке функции. Например:

int& count

В вызове такой функции достаточно указать имя переменной и она будет передана по ссылке. Реально в функцию передается не сама переменная, а ее адрес в памяти, полученный операцией адресации (&). Тогда все изменения, производимые в функции с таким параметром, будут отражаться в значении фактического параметра.

Например:

void square(int&);//прототип функции вычисления квадрата

void square(int& a) //заголовок функции

{

a *= a;

}

Вызываться подобная функция может обычным способом передачей в нее имени аргумента. Например:

int x1 = 2;

square(x1);

В результате подобного вызова переменная x1 получит значение 4.

Если параметром функции является массив, то знак ссылки указывать не нужно, передача параметра по ссылке происходит автоматически. Также не следует для формального параметра-массива указывать в квадратных скобках его размер (ставятся пустые скобки). Размер же можно передать отдельным параметром.

Передача в качестве параметров функций матриц осуществляется через указатели и будет рассматриваться в следующем семестре.

Параметры со значениями по умолчанию

Обычно при вызове функции в нее передается конкретное значение каждого параметра. Но при разработке программы можно указать, что параметр является параметром по умолчанию, и приписать этому параметру значение по умолчанию. Делается это заданием в заголовке функции после имени параметра символа «=», после которого записывается значение по умолчанию. Например, опишем функцию вычисления площади треугольника по трем сторонам (формула Герона):

double Area(double a=1.0, double b=1.0, double c=1.0)

{

double p = (a+b+c)/2;

return sqrt(p*(p-a)*(p-b)*(p-c));

}

Здесь всем трем параметрам-сторонам даны значения по умолчанию, равные 1.

Если при вызове функции параметр по умолчанию не указан, то в функцию автоматически передается его значение по умолчанию. Например, если вызвать приведенную функцию оператором

S = Area();

то значение S будет равно площади при значениях всех сторон по умолчанию.

Аргументы по умолчанию должны быть самыми правыми (последними) аргументами в списке параметров функции. Например, вызов той же функции оператором

S = Area(1.5);

позволяет рассчитать площадь треугольника, если длина одной стороны равна 1,5, а остальные длины берутся по умолчанию.

Примеры программ

1. Программа нахождения и печати значений функции в заданном диапазоне : 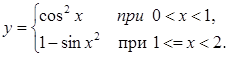Dx=0.2.

Функция Func1 Функция Func2

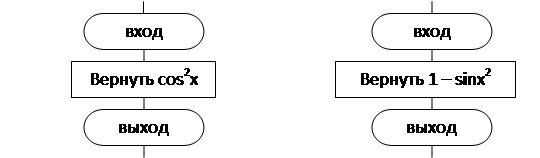
Главная функция программы

#include <iostream.h>

#include <math.h>

double Func1(double x)

{

return pow(cos(x),2);

}

double Func2(double x)

{

return 1-sin(x*x);

}

void main()

{

const double dx=0.2;

double x,y;

x = 0;

while (x<1)

{

y = Func1(x);

cout<<y<<' ';

x += dx;

}

cout<<endl;

while (x<2)

{

y = Func2(x);

cout<<y<<' ';

x += dx;

}

cout<<endl;

}

2. Программа заполнения и нахождения суммы элементов одномерного массива.

Функция Generate Функция Summa

Главная функция программы

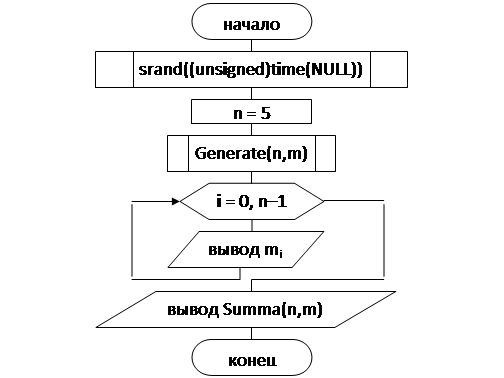
#include <iostream.h>

#include <stdlib.h>

#include <time.h>

void Generate(int N, int mas[])

{

for (int i=0;i<N;i++)

mas[i] = rand()%100;

}

int Summa(int N, int mas[])

{

int s = 0;

for (int i=0;i<N;i++)

s += mas[i];

return s;

}

void main()

{

srand((unsigned)time(NULL));

const n=5;

int m[n];

Generate(n,m);

for (int i=0;i<n;i++)

cout<<m[i]<<' ';

cout<<"\nSumma = "<<Summa(n,m)<<endl;

}

Варианты заданий

Вариант 1

1. В массиве точек на плоскости найти пару точек с максимальным расстоянием между ними. Определить функцию нахождения расстояния между точками.

2. Описать функции ввода с клавиатуры элементов одномерного массива и нахождения произведения сумм элементов массива с четными и нечетными номерами.

Вариант 2

1. Расстояние между двумя множествами точек - это расстояние между наиболее близко расположенными точками этих множеств. Найти расстояние между двумя заданными множествами точек на плоскости.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения количества элементов, у которых значения предыдущего и последующего элемента равны? Например: 2 3 2 4 5 4 7 8 9 – таких элементов два, это 3 и 5.

Вариант 3

1. Многоугольник задан на плоскости множеством координат вершин в порядке обхода его границ. Определить площадь многоугольника.

2. Описать функции ввода с клавиатуры элементов одномерного массива и определения суммы четных элементов с четными номерами, например: V[2]=10.

Вариант 4

1. Выбрать три разные точки заданного на плоскости множества точек, составляющие треугольник наибольшего периметра.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения количества чисел, состоящих из одинаковых цифр? Например: 11, 55 и т.д.

Вариант 5

1. Найти такую точку заданного на плоскости множества точек, сумма расстояний от которой до остальных минимальна.

2. Описать функции ввода с клавиатуры элементов одномерного массива и подсчета произведения элементов массива V, значения которых совпадают с их номерами, например: V[3]=3.

Вариант 6

1. Даны отрезки а, b, с и d. Для каждой тройки этих отрезков, из которых можно построить треугольник, напечатать площадь данного треугольника. (Определить функцию, вычисляющую площадь треугольника, если она существует).

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и изменения всех элементов массива на противоположные по знаку

Вариант 7

1. Для натуральных a и b операцию Ä определим так:

a Ä b = a – b + a % b

Найти все такие пары a, b, не превосходящие заданного n, для которых a Ä b = b Ä a.

2. Описать функции ввода с клавиатуры элементов одномерного массива. Поменять местами минимальный и максимальный элементы массива.

Вариант 8

1. По введенному целому числу М распечатать все трехзначные десятичные числа, сумма цифр равна М. Подсчитать также количество таких чисел или сообщить о том, что их нет. (Описать функцию вычисления суммы цифр числа).

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения суммы элементов, принадлежащих заданному диапазону.

Вариант 9

1. Вычислить, не используя функцию pow(), значения функции

z (x, m) = x^m × sin^m (xm)

для значений аргументов: x от –1.1 до 0.3 с шагом 0.2; m от 1 до 5 с шагом 1.

2. Описать функции ввода с клавиатуры элементов одномерного массива и определения количества нулей в этом массиве.

Вариант 10

1. Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами, и квадратом третьей цифры.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения суммы его элементов, лежащих между его максимальным и минимальным элементами.

Вариант 11

1. Треугольник задан координатами своих вершин. Найти его периметр и площадь. (Описать функцию вычисления длины стороны).

2. Описать функции ввода с клавиатуры элементов одномерного массива и определения произведения его элементов, лежащих между его первым и последним нулями.

Вариант 12

1. Описать функцию ттах(х,у), которая при­сваивает первому параметру большее, а второму – меньшее из значений х и у. Используя эту функцию, перераспределить введенные значения переменных А, В, С так, чтобы стало А < В < С.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и проверки равенства двух массивов.

Вариант 13

1. Выяснить, сколько простых чисел находится в интервале [т,п], и распечатать их. Для определения, является ли очередное число простым, составить функцию.

2. Описать функции ввода с клавиатуры элементов одномерного массива. Вычислить сумму длин двух векторов. Длина вектора вычисляется по формуле: .

Вариант 14

1. Даны вещественные числа а, b, с, d, е, f. Переменной s присвоить значение 1, если оба уравнения ах² + bх + с = 0 и dx² + ex + f = 0 имеют вещественные корни и при этом все корни первого уравнения лежат между корнями второго уравнения. В противном случае переменной s присвоить значение 0. (Для нахождения корней квадратного уравнения использовать функцию).

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и замены нечетных элементов на заданное число.

Вариант 15

1. Найти натуральное число из интервала [n1,n2] с максимальной суммой делителей. (Для нахождения суммы делителей числа использовать функцию).

2. Описать функции ввода с клавиатуры элементов одномерного массива и нахождения суммы и разности всех элементов с четными и нечетными номерами соответственно.

Вариант 16

1. Найти все двузначные числа, сумма цифр ко­торых не меняется при умножении числа на 2.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и сортировки массива методом пузырька.

Вариант 17

1. Напечатать все трёхзначные натуральные числа, в десятичной записи которых нет двух одинаковых цифр и они упорядочены по возрастанию слева направо.

2. Описать функции ввода с клавиатуры элементов одномерного массива и сдвига его элементов по правилу 1®2®…n®1.

Вариант 18

1. Дано натуральное число N>19, распечатать четверки простых чисел, не превосходящих N, принадлежащих одному десятку. Например, для числа 112 надо напечатать четверки

2 3 5 7

11 13 17 19

101 103 107 109

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и нахождения суммы двух массивов.

Вариант 19

1. Два натуральных числа называются дружественными, если каждое из них равно сумме простых делителей другого. Найти все пары дружественных чисел в диапазоне [n1,n2].

2. Описать функции ввода с клавиатуры элементов одномерного массива и определения того, образуют ли элементы массива неубывающую последовательность (функция должна возвращать «0», если все в порядке, или индекс первого элемента массива, на котором условие нарушается.)

Вариант 20

1. Дано натуральное число n>13. Выдать все пары простых чисел, разность между которыми равна 4, а сами числа меньше n.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения среднеарифметического значения элементов и максимального отклонения от него.

Вариант 21

1. Определить, сколько чисел между m и n (m<n) состоит из нечетных цифр.

2. Описать функции ввода с клавиатуры элементов одномерного массива и сортировки его таким образом, чтобы все положительные числа находились в начале, а отрицательные – в конце массива и был сохранен исходный порядок следования элементов в обеих группах.

Вариант 22

1. Написать функцию перевода времени, заданного в секундах или минутах в часы, минуты, секунды. Предусмотреть выбор варианта: секунды или минуты.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и нахождения пары соседних эле­ментов, наиболее близко расположенных друг к другу. Мера близости:

R = ½A[i+1] - A[i]½.

Вариант 23

1. Даны длины сторон a, b и с треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Предусмотреть функцию проверки существования исходного треугольника. (Примечание: длина медианы, проведенной к стороне а, равна ).

2. Описать функции ввода с клавиатуры элементов одномерного массива и нахождения суммы элементов массива, предшествующих первому отрицательному элементу. Если среди элементов массива нет отрицательных, то про­суммировать все элементы.

Вариант 24

1. Выяснить, сколько совершенных чисел находится в диапазоне [5..2000]. Число является совершенным, если оно равно сумме всех своих делителей, кроме самого себя (например, число 6 совершенно: 6=1+2+3).

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения, сколько раз в нем встретились два подряд идущих нулевых элемента.

Вариант 25

1. Найти: y=среднее(a,b,c,d)/(min(a,b,c)+min(a,d).

2. Описать функции ввода с клавиатуры элементов одномерного массива и поиска минимума среди тех элементов массива Х, которые не являются элементами массива Y.

Вариант 26

1. Дана последовательность из не менее чем двух натуральных чисел, за которой следует 0. Вычислить сумму тех из них, порядковые номера которых - простые числа. Для определения того, является ли число простым, использовать функцию.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения максимума из чисел, встречающихся в этом массиве более одного раза.

Вариант 27

1. Определить количество чисел-палиндромов из заданного диапазона. Палиндромом называется число, десятичная запись которого читается слева направо и справа налево одинаково.

2. Описать функции ввода с клавиатуры элементов одномерного массива и замены в нем каждой группы из подряд идущих нулей на 2 элемента: первый из них 0, а второй – количество нулей в данной группе.

Вариант 28

1. Найти все натуральные числа, не превосходящие n и делящиеся на каждую из своих цифр.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и сдвига элементов массива на k позиций вправо. Элементы, выходящие за границу массива, теряются. Освободившиеся в массиве позиции заполняются нулями.

Вариант 29

1. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенная в степень n, равна самому числу. Подсчитать все числа Армстронга из двух и трех цифр.

2. Описать функции ввода с клавиатуры элементов одномерного массива и замены в нем каждой группы из нечетного количества подряд идущих нулей на один нуль, а из четного количества – на два.

Вариант 30

1. Подсчитать количество «счастливых» шестизначных билетов в рулоне, если номер первого билета m, а количество билетов n.

2. Описать функции формирования элементов одномерного массива с помощью генератора случайных чисел и определения количества инверсий в этом массиве (т.е. таких пар элементов, в которых большее число находится слева от меньшего: x_i>x_i+1).