Действия над матрицами

Глава 1. ЛИНЕЙНАЯ АЛГЕБРА.

Лекция 1. Матрицы. Виды матриц. Действия над матрицами.

На данном занятии будут рассмотрены такие важные понятия:

ü Матрицы.

ü Виды матриц.

ü Действия над матрицами.

Определение. Матрицейразмером называется прямоугольная таблица из элементов произвольной природы, которая записывается в виде:

,

где - число строк матрицы, - число столбцов матрицы, 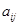- элемент матрицы, расположенный на пересечении 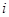- ой строки и - ого столбца матрицы ( ).

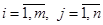Обычно матрицы обозначаются большими буквами латинского алфавита и для краткости пишут:

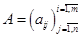, или , а иногда и без разъяснени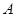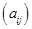й , или .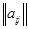

В дальнейшем мы будем рассматривать только числовые матрицы, т.е. матрицы, все элементы которых являются числами.

Определение.Две матрицы называются равнымимежду собой, если они имеют одинаковые размеры и равны их соответствующие элементы.

Определение.Матрица размера 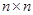(число строк равно числу столбцов и равно ) называется квадратной матрицей - ого порядка, т.е.

.

Определение.Для квадратных матриц существуют понятия главной диагонали и побочной диагонали. Главная диагональ идет из левого верхнего угла в правый нижний, а побочная диагональ – из левого нижнего угла в правый верхний.

Определение.Квадратная матрица называется верхней треугольной матрицей, если все ее элементы, расположенные под главной диагональю равны нулю, т.е.

.

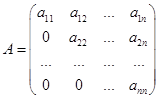Определение.Квадратная матрица называется нижней треугольной матрицей, если все ее элементы, расположенные над главной диагональю равны нулю, т.е.

.

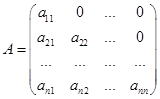Определение.Квадратная матрица называется диагональной матрицей(обозначается 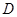), если все ее элементы вне главной диагонали равны нулю, т.е.

.

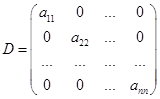Определение.Диагональная матрица называется единичной матрицей(обозначается 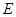), если все ее элементы на главной диагонали равны 1, т.е.

.

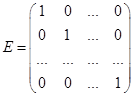Определение.Матрица, у которой все элементы равны нулю, называется нулевой матрицей(обозначается 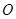), т.е.

.

В матричном исчислении матрицы 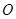и 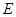играют роль и в арифметике.

Определение.Матрица, состоящая только из одной строки, называется вектор-строкой, т.е. .

Определение.Матрица, состоящая только из одного столбца, называется вектор-столбцом, т.е. .

Определение.Матрица называется транспонированной по отношению к матрице 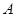, если она получается из матрицы 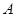путем замены всех ее строк соответствующими столбцами, т.е.

.

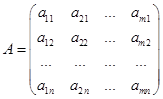Таким образом, если размер исходной матрицы , то размер транспонированной по отношению к ней матрицы .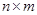

Например, если , то 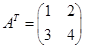. Если 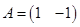, то .

Действия над матрицами.

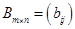Определение. Суммой двух матриц и называется матрица , элементы которой определяются равенством , где .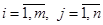

Обозначается эта операция .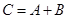

Заметим, что операция суммы двух матриц вводится только для матриц одного размера, и результирующая матрица имеет тот же размер, что и матрицы-слагаемые.

Например, .

Аналогично определяется разность двух матриц .

Операция сложения матриц обладает следующими свойствами:

1. ;

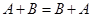2. ;

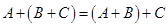3. .

Определение. Произведением матрицы на число 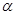называется матрица 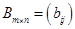, элементы которой определяются равенством 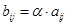, где .

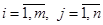Обозначается эта операция или , или .

Например, .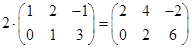

Определение.Матрица 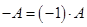называется противоположной матрице .

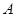Операция произведения матрицы на число обладает следующими свойствами:

1. ;

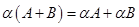2. ;

3. ;

4. ;

5. .

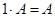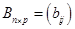Определение. Произведением матрицы на матрицу называется матрица 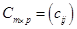, элементы которой определяются равенством , где 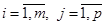, т.е. элемент 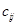равен сумме произведений элементов 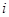-ой строки матрицы 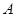на соответствующие элементы -ого столбца матрицы .

Обозначается эта операция 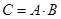или .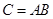

Заметим, что операция произведения двух матриц вводится только для матриц, у которых число столбцов первой матрицы-множителя равно числу строк второй матрицы-множителя, а результирующая матрица имеет размер: число строк первой матрицы-множителя на число столбцов второй матрицы-множителя.

Например, .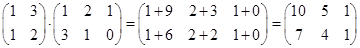

В общем случае, равенство не выполняется!

Определение.Матрицы 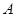и называются перестановочными, если .

Операция произведения матриц обладает следующими свойствами:

1. или ;

2. ;

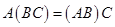3. ;

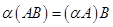4. или ;

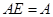5. или .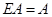

Операция транспонирования матриц обладает следующими свойствами:

1. ;

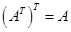2. ;

3. .

Контрольные вопросы:

1. Сформулируйте определение матрицы. Приведите примеры.
2. Что называется размером матрицы?
3. Какие существуют основные обозначения матриц?
4. Сформулируйте определение квадратной матрицы. Приведите примеры.
5. Что называется главной диагональю матрицы?
6. Что называется побочной диагональю матрицы?
7. Сформулируйте определение верхней треугольной матрицы. Приведите примеры.
8. Сформулируйте определение нижней треугольной матрицы. Приведите примеры.
9. Сформулируйте определение диагональной матрицы. Какое обозначение существует для диагональных матриц? Приведите примеры.
10. Сформулируйте определение единичной матрицы. Какое обозначение существует для единичных матриц? Приведите примеры.
11. Сформулируйте определение нулевой матрицы. Какое обозначение существует для нулевых матриц? Приведите примеры.
12. Сформулируйте определение транспонированной матрицы. Как обозначаются транспонированные матрицы? Приведите примеры. Какими свойствами обладает эта операция?
13. Какие две матрицы называются равными? Приведите примеры.
14. Сформулируйте определение суммы двух матриц. Приведите примеры. Какими свойствами обладает эта операция?
15. Сформулируйте определение произведения матрицы на число. Приведите примеры. Какими свойствами обладает эта операция?
16. Сформулируйте определение произведения двух матриц. Приведите примеры. Какими свойствами обладает эта операция?
17. Какие две матрицы называются перестановочными?