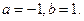Общее уравнение прямой на плоскости
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
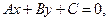
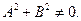 Это уравнение называют общим уравнением прямой.
Это уравнение называют общим уравнением прямой.
В зависимости от значений постоянных 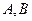 и
и 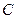 возможны следующие частные случаи:
возможны следующие частные случаи:
- 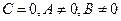 – прямая проходит через начало координат;
– прямая проходит через начало координат;
- 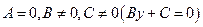 - прямая параллельна оси
- прямая параллельна оси 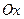 ;
;
- 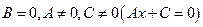 – прямая параллельна оси
– прямая параллельна оси 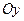 ;
;
- 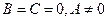 – прямая совпадает с осью
– прямая совпадает с осью 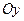 ;
;
- 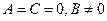 – прямая совпадает с осью
– прямая совпадает с осью 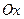 .
.
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и нормальному вектору
В декартовой прямоугольной системе координат вектор с координатами 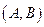 перпендикулярен прямой, заданной уравнением
перпендикулярен прямой, заданной уравнением 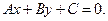 Он называется нормальным вектором прямой.
Он называется нормальным вектором прямой.
Пример. Найти уравнение прямой, проходящей через точку 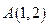 перпендикулярно вектору
перпендикулярно вектору 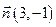 .
.
Для  и
и 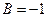 уравнение прямой примет вид:
уравнение прямой примет вид: 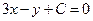 . Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем
. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем 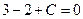 . Следовательно
. Следовательно 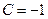 . Искомое уравнение запишется в виде
. Искомое уравнение запишется в виде 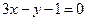 .
.
Уравнение прямой по точке и угловому коэффициенту
Если общее уравнение прямой 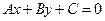 привести к виду:
привести к виду:
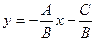 ,
, 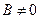
и обозначить 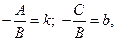 т.е.
т.е. 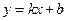 , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
, то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору
Определение. Каждый ненулевой вектор 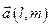 , компоненты которого удовлетворяют условию
, компоненты которого удовлетворяют условию 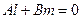 называется направляющим вектором прямой
называется направляющим вектором прямой 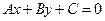 .
.
Пример.Найти уравнение прямой с направляющим вектором 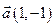 и проходящей через точку
и проходящей через точку 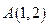 .
.
Уравнение искомой прямой будем искать в виде: 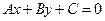 . В соответствии с определением, коэффициенты должны удовлетворять условиям:
. В соответствии с определением, коэффициенты должны удовлетворять условиям:
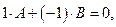 т.е.
т.е. 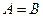 .
.
Тогда уравнение прямой имеет вид: 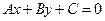 , или
, или 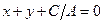 .
.
при 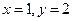 получаем
получаем 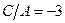 , т.е. искомое уравнение имеет вид
, т.е. искомое уравнение имеет вид 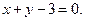
Уравнение прямой на плоскости, проходящей через две данные точки
Рассмотрим прямую в пространстве, проходящую через заданную точку 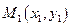 , с направляющим вектором
, с направляющим вектором 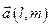 :
:
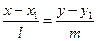 .
.
Пусть 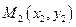 - произвольная точка этой прямой. Тогда выполняются равенства:
- произвольная точка этой прямой. Тогда выполняются равенства:
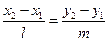 ,
,
Решая совместно эти уравнения, получим:
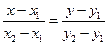
-уравнение прямой, проходящей через две точки 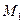 и
и 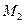 на плоскости.
на плоскости.
Замечание. Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
Пример. Найти уравнение прямой, проходящей через точки 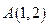 и
и 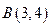 . Имеем
. Имеем
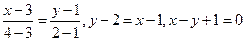 .
.
7. Уравнение прямой в отрезках
Если в общем уравнении прямой 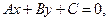
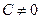 то, разделив на
то, разделив на 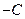 , получим:
, получим: 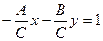 или
или 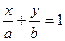 , где
, где 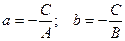 .
.
Геометрический смысл коэффициентов: коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой 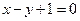 . Найти уравнение этой прямой в отрезках.
. Найти уравнение этой прямой в отрезках.
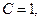
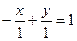 ,
,