Векторное произведение векторов

Векторным произведением векторов и называется вектор 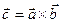, определяемый следующим образом:

1)

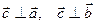
2)

3) векторы 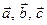образуют правую тройку.

С помощью векторного произведения можно находить:

1) Вектор, перпендикулярный плоскости, которой параллельны векторы и

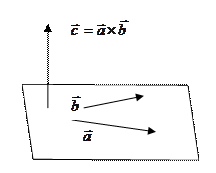
2) Площадь параллелограмма и треугольника, построенного на векторах и соответст-

венно по формулам:

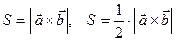
Вычисляется векторное произведение с помощью определителя:

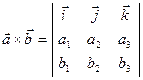
Пример. Найти векторное произведение векторов и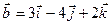

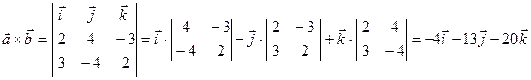
Проверим вычисления. Так как 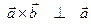и , то надо убедиться, что скалярные произведения равны нулю:

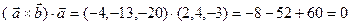
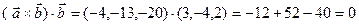
Пример. Найти площадь треугольника с вершинами

Найдем координаты векторов 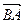, 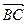: . Затем находим векторное произведение:

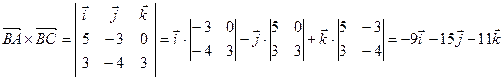
Проверим вычисления:

Аналогично,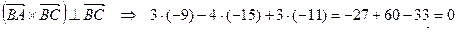

Находим площадь треугольника:

.

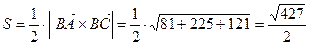Задание 3.

1) Найти вектор 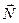, перпендикулярный вектору и вектору .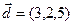

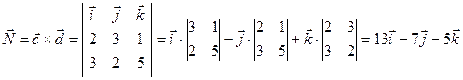
Ответ: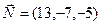

2) Найти площадь треугольника с вершинами .

Находим координаты векторов, на которых построен этот треугольник:

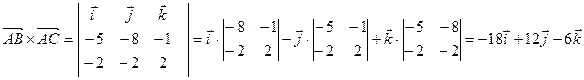
Ответ: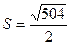

Смешанное произведение векторов.

Смешанным произведением векторов 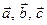называется число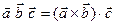

Вычисляется смешанное произведение векторов по формуле

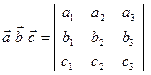
С помощью смешанного произведения можно находить:

1) Объем параллелепипеда, построенного на векторах :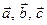

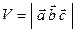
2) Объем тетраэдра, построенного на векторах :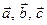

Пример. Найти объем тетраэдра с вершинами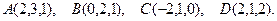

Находим смешанное произведение векторов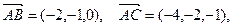

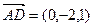на которых построен этот тетраэдр.

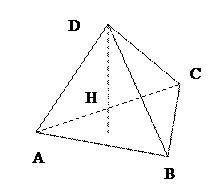
Задание 4.Найти объем тетраэдра ABCD с вершинами и найти длину его высоты, проведенной из вершины D.

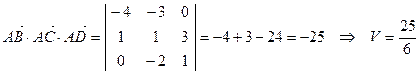
С другой стороны, объем пирамиды можно найти по формуле . Выразим отсюда искомую высоту: 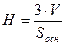. Объем уже известен, а площадь треугольника ABC найдем с помощью векторного произведения векторов .

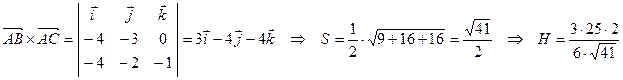
Ответ: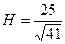

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

Задание 1Проверить, что векторы образуют базис и разложить вектор 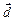по этому базису.

Вариант 1.

Вариант 2.

Вариант 3.

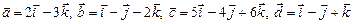
Вариант 4.

Вариант 5.

Вариант 6.

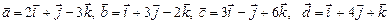
Вариант 7.

Вариант 8.

Вариант 9.

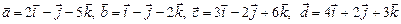
Вариант 10.

Задание 2В треугольнике АВС найти периметр Р, косинус угла при вершине В, проекцию вектора 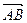на вектор .

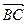Вариант 1. А(2,3,1), В(0,-3,2), С(3,6,2)

Вариант 2. А(2,-4,-1), В(0,-3,-2), С(1,6,2)

Вариант 3. А(2,-3,1), В(0,-3,1), С(3,-4,2)

Вариант 4. А(2,-5,1), В(0,-1,2), С(3,1,2)

Вариант 5. А(-2,3,-1), В(1,-7,2), С(0,6,2)

Вариант 6. А(2,-5,1), В(0,9,2), С(-1,6,2)

Вариант 7. А(0,3,1), В(-2,-3,2), С(-3,2,2)

Вариант 8. А(0,5,1), В(-2,-6,2), С(-3,1,2)

Вариант 9. А(0,3,-1), В(-2,-3,2), С(-3,2,-2)

Вариант 10. А(-2,3,0), В(-2,12), С(-3,2,-6)

Задание 31)Найти площадь 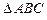(координаты вершин смотри в задании 2) 2) Найти вектор 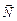, перпендикулярный двум заданным векторам и

Вариант 1.

Вариант 2.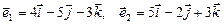

Вариант 3.

Вариант 4.

Вариант 5.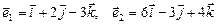

Вариант 6.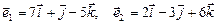

Вариант 7.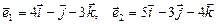

Вариант 8.

Вариант 9.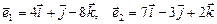

Вариант 10.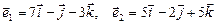

Задание 4В тетраэдре 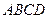найти объем и длину высоты, проведенной из вершины С на грань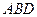

Вариант 1. А(2,3,1), В(0,-3,2), С(3,6,2), D(3,6,1)

Вариант 2. А(2,-4,-1), В(0,-3,-2), С(1,6,2), D(4,9,3)

Вариант 3. А(2,-3,1), В(0,-3,1), С(3,-4,2), D(0,3,-2)

Вариант 4. А(2,-5,1), В(0,-1,2), С(3,1,2), D(2,6,1)

Вариант 5. А(-2,3,-1), В(1,-7,2), С(0,6,2), D(-3,5,1)

Вариант 6. А(2,-5,1), В(0,9,2), С(-1,6,2), D(0,3,1)

Вариант 7. А(0,3,1), В(-2,-3,2), С(-3,2,2), D(-3,6,7)

Вариант 8. А(0,5,1), В(-2,-6,2), С(-3,1,2), D(2,-5,4)

Вариант 9. А(0,3,-1), В(-2,-3,2), С(-3,2,-2), D(2,8,6)

Вариант 10. А(-2,3,0), В(-2,12), С(-3,2,-6), D(-2,0,1)