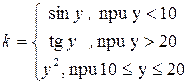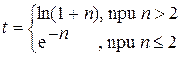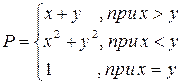Вычислить и вывести на печать значения функции

Протабулировать функцию

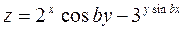
для xÎ[-1;1] с Dx=0,4; yÎ[1;2] с Dy=0,3.

3. Задан одномерный массив Р(N) (N<=60). Если в нём больше отрицательных чисел, все положительные числа заменить суммой отрицательных, полученный массив распечатать. Если больше неотрицательных чисел, то вывести об этом сообщение.

4.Получить массив D( MxN), М<=10, N<=20 по формуле

D_I,J = max(A_I,J, B_I,J+C_I,J).

Вывести массив D на экран. Массивы A(MxN), B(MxN), C(MxN) заданы.

5. Ввести файл F целых чисел. Заменить в нем каждую вторую компоненту, значение которой кратно пяти, на число А. Выдать файл до преобразования и после него. Если преобразование файла невозможно, то выдать сообщение об этом, указав причину.

ВАРИАНТ 10

1. Определить, значения каких из целочисленных переменных a,b,c кратны 3. Если все три значения кратны 3 ,то вычислить их сумму, в противном случае значения a,b,c утроить.

2. Протабулировать функцию

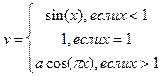
x принадлежит отрезку [-1;3] с шагом 0,5.

3. В заданном одномерном массиве А(N) (N<=50) вычислить сумму отрицательных элементов массива, находящихся после минимального элемента. Если таких элементов нет, то вывести об этом сообщение.

4. Задана матрица Х[N,N], где N<=15. Положительные элементы строк с четными номерами разделить на максимальный элемент побочной диагонали. Преобразованную матрицу вывести на экран.

5. Дан файл F. Все его отрицательные компоненты увеличить в два раза, положительные уменьшить в три раза, на место нулевых компонент записать их количество. В преобразованном файле найти максимальное значение. Файл F распечатать.

ВАРИАНТ 11

1. Дано: x и y. Вычислить z=x²-5xy+tg y, если y¹0. Если y=0, выдать сообщение «y=0». Если z<10, и напечатать b=12y+e^x+5. Если z³10, вычислить и напечатать c=x²+y²-17,5.

Вычислить и вывести на печать значения функции

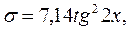
где xÎ[0,1;7,6] с Dx=0,5.

3. Задан одномерный массив А(N) (N<=60). На место минимального элемента массива записать сумму последних К элементов массива. Если А [1]>=0, то умножить все элементы этого массива на квадрат минимального элемента данного вектора, а если А[1]<0, то умножить все элементы на квадрат максимального элемента вектора. Полученный массив распечатать.

4. Вычислить сумму элементов главной диагонали матрицы В (MxМ), М<=18. Если сумма окажется >10 , то исходную матрицу преобразовать по формуле

В(I,J) = В(I,J) + 3.5,

если сумма будет £10, то преобразование выполнить по формуле

В(I,J) = В(I,J) – 3.5.

Вычисленную сумму и элементы преобразованной матрицы вывести на экран.

5 Задан числовой файл F. Найти сумму компонент, стоящих между минимальной и максимальной. Записать в файл H сначала минимум, затем максимум, затем сумму. Файл H распечатать.

ВАРИАНТ 12

1. Дано a, b, x. Вычислить и напечатать: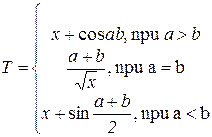

Если T>0, то вычислить и напечатать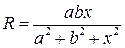

Если T£0, то напечатать a, b, x.

2. Вычислить и вывести на печать таблицу значений функции

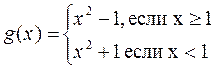
на отрезке [-3;3] с Dx=0,5.

3. Дан одномерный массив Х(N) (N<=60). На место отрицательных элементов массива записать среднее арифметическое максимального и минимального элементов. Результат вывести на экран.

4. В заданной квадратной матрице A(K,K) (K£10) вычислить сумму элементов, расположенных над главной диагональю. Полученной суммой заменить минимальный элемент всей матрицы. Сумму и матрицу распечатать.

5. Задан числовой файл F. Найти максимум среди компонент, расположенных на четных позициях файла. Все нулевые компоненты заменить значением максимума. Преобразованный файл F распечатать.

ВАРИАНТ 13

1. Даны y, x, a, b. Вычислить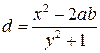

Если d=0, напечатать y, x, a, b.

Если d>0, то вычислить и напечатать P=e^2x · sin y – 3.

Если d<0, то увеличить в 2 раза y, x, a, b и напечатать.

2.Ввести В. Если В<10, выдать на печать 2*В. Если В>=10, вычислить и напечатать значения функции y=x²-x+tg(1/B+x) для значений x, изменяющихся от –3 до 1, с шагом 0,1.

3. Дан массив Х(N) (N<=60). Получить массив М по правилу:

M[i]=

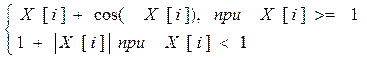
Найти значения и индексы минимального и максимального элементов массива М.

4. Задана матрица Х[N,N], где N<=15. В каждом столбце матрицы поменять местами минимальный элемент и элемент главной диагонали. Преобразованную матрицу вывести на экран.

5. Ввести числовой файл F1 выдать его на печать. Определить в нем среднее арифметическое отрицательных компонент и заменить им минимальную компоненту файла. Выдать на печать преобразованный файл или сообщение о невозможности преобразования.

ВАРИАНТ 14

1.

Рассчитать y=x²+1,8 при заданном x. Далее вычислить и напечатать

2. Вычислить значения функции 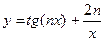при n=1,2, … ,20 и изменении x в интервале [1; 3] c шагом Dх=0,2. Отпечатать только значения функции y > 15.

3. Дан вектор А(N) (N<=60). Разделить каждую компоненту вектора на разность между максимальной и минимальной компонентой данного вектора. Результирующий вектор упорядочить по убыванию и отпечатать.

4. Преобразовать исходную матрицу L (MxN), М<=10, N<=20 путем сложения ее элементов с произведением элементов того столбца, который содержит минимальный элемент всей матрицы. Преобразованную матрицу L отпечатать.

5. Ввести файл целых положительных чисел F1. Компоненты файла F1, меньшие числа M, записать в файл F2. В файле F1 этим компонентам присвоить значение нуль. Выдать на печать файлы F1 и F2.

ВАРИАНТ 15

1.

Дано l, m, n. Если l<m , вычислить и отпечатать

Если l³m, то вычислить и отпечатать k=ml²-cos n.

2. Вычислить и напечатать значения функции y=e^at 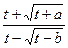при изменении t на интервале [2;4] с шагом 0.2; a=0.5;b=1.3.

3. Задан одномерный массив F(N) (N<=60).Вычислить произведение минимального и максимального элементов массива и заменить им элемент массива стоящий перед минимальным элементом. Если такого элемента нет, то выдать соответствующее сообщение. Результат вывести на экран.

4. В массиве Р(N,M) (N£10; M£15) поменять местами минимальный и максимальный элементы каждой строки.

5. Ввести файл F действительных чисел. Заменить в нем максимальный и минимальный компоненты на значение среднего арифметического всех положительных компонент файла. Выдать на печать файл до преобразования и после. В случае невозможности преобразования дать об этом сообщение.

ВАРИАНТ 16

1. Дано a, b, c, x.

Если a²+b<c, рассчитать M=cos²x – tg x.

При M>0 рассчитать и отпечатать T=e^x-12,4x².

При M£0 рассчитать и отпечатать Q=½x³½-7,15x³.

Если a²+b³c, рассчитать N=sin²x+tg x.

При N>1 рассчитать и отпечатать P=e^–X+6,83x.

При N£1 рассчитать и отпечатать R=ln x +6,2e^X.

2. Вычислить значение 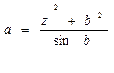. Если а<0, выдать на печать a. Если a>=0,вычислить и напечатать значения функции y=(x²-1)sinx, где х изменяется на интервале (-2,+2) с шагом 0,25.

3. Дан одномерный массив Х(N) (N<=60). На место минимального элемента массива записать сумму последних K элементов массива. Результат вывести на экран.

4. Задана матрица Х[N,M], где N<=15, M<=20. В каждой строке матрицы А найти среднее арифметическое элементов, принадлежащих интервалу [-5; 5] и из найденных значений сформировать одномерный массив Y. Массив Y вывести на экран.

5. Ввести с клавиатуры файл F действительных чисел и выдать его на печать. Определить в нем среднее арифметическое компонентов, стоящих после второй отрицательной компоненты, и записать его в конец файла. Выдать на печать преобразованный файл. Если преобразование невозможно, то дать об этом сообщение.

ВАРИАНТ 17

1. Задать R и P. Если R>P, то вычислить и напечатать z=R-P, иначе z=P-R. Вычислить и распечатать при различных значениях z:

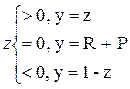
2. Рассчитать функцию 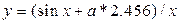при изменении аргумента на отрезке [1;5] с шагом dx=0.123 и вывести на печать значение у>0.1.

3. Задан одномерный массив A(N) (N<=60). Посчитать сумму элементов, находящихся между максимальным и минимальным элементами. Результат вывести на печать.

4. Задана матрица Х[N,N], где N<=15. В каждой строке матрицы поменять местами минимальный элемент и элемент побочной диагонали. Преобразованную матрицу вывести на экран.

5.Дан файл G, компонентами которого являются вещественные числа. Найти в нем максимальную и минимальную компоненты и поменять их местами. Преобразованный файл G распечатать в обратном порядке.

ВАРИАНТ 18

1. Ввести z. Если z>0, то вычислить и напечатать 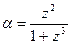, если z=0, то выдать соответствующее сообщение, если z<0, то вычислить и напечатать 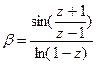. Если 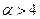, то выдать соответствующее сообщение, иначе посчитать и распечатать .

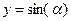2. Вычислить значения функции a=1.6x³-1.5 на интервале [-1,1] с шагом изменения аргумента 0.5. Выдать на печать отрицательные значения функции с соответствующими им значениями аргумента.

3. Задан одномерный массив R(N) (N<=60). Получить новый массив Q путём домножения элементов исходного массива R на его минимальный элемент. Вычислить среднее арифметическое полученного массива Q и записать его на место минимального элемента исходного массива R. Результат вывести на экран.

4. Задана матрица Х[N,M], где N<=15, M<=20. Найти среднее арифметическое элементов строк с четными номерами. Если найденное среднее положительно, то все отрицательные элементы матрицы заменить их модулями. В противном случае все положительные элементы матрицы заменить нулем. Преобразованную матрицу вывести на экран.

5. Дан файл G, компонентами которого являются вещественные числа. Найти сумму и количество компонент, расположенных на нечетных позициях файла. Сумму записать на место первой компоненты файла. Преобразованный файл G, а также найденные сумму и количество распечатать.

ВАРИАНТ 19

1. Дано m, n, t, k. Если m²>n², вычислить и отпечатать

Z=1,12 sin t при k=1

X=2,2 cos t² при k=2

Y=7,35 ln t³ при k=3

Иначе рассчитать и отпечатать А=m² sin t + n² cos t.

2. Выполнить табулирование функции

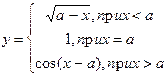
на отрезке [9;10] с шагом 0,1.

3. Задан одномерный массив X(N) (N<=50). Вычислить среднее геометрическое положительных элементов массива, считая, что в массиве есть положительные элементы. Все отрицательные элементы массива заменить найденным значением. Преобразованный массив распечатать.

4. Задана матрица Х[N,M], где N<=15, M<=20. Сформировать одномерный массив Y из минимальных элементов столбцов матрицы Х. Все отрицательные элементы массива Х заменить их модулями. Массив Х вывести на экран.

5. В файле F заменить все нулевые компоненты значением суммы первой и последней компонент файла; все отрицательные компоненты уменьшить на значение суммы, а также найти среднее арифметическое положительных компонент. Результаты отпечатать.

ВАРИАНТ 20

1. Дано a, b, x. Вычислить и напечатать: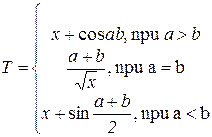

Если T>0, то вычислить и напечатать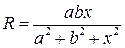

Если T£0, то напечатать a, b, x.

2. Вычислить и вывести на печать таблицу значений функции

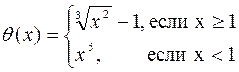
на отрезке [-3;3] с Dx=0,5.

3. Задан одномерный массив А(N) (N<=90). Поменять местами максимальный и минимальный элементы массива A(N). Преобразованный массив вывести на экран.

4. Ввести двумерный массив A(N,N) (N£10). Поменять в нем местами максимальный элемент побочной диагонали и максимальный элемент всего массива. Выдать на печать преобразованный массив.

5. Ввести файл F действительных чисел и выдать его на печать. Преобразовать его, не создавая нового файла, разделив каждую его компоненту на значение максимума. Выдать на печать преобразованный файл. Если преобразование файла невозможно, то выдать об этом сообщение.

ВАРИАНТ 21

1. Вычислить y=16x²-1 при заданном x.

Если y>=3, то вычислить и напечатать b=x³; если y<3 ,то вычислить и напечатать c=10-x. Если b>0, увеличить у в 2 раза и вывести на экран, в противном случае выдать об этом сообщение.

2. Выполнить табулирование функции

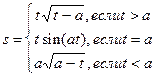
t принадлежит отрезку [1;5], шаг изменения 0,5; а=2,5

3. В заданном одномерном массиве X(N) (N<=70) наибольший и наименьший элементы увеличить в три раза, а все остальные – в два раза. Исходный массив и преобразованный распечатать один под другим.

4. Задана матрица Х[N,N], где N<=15. Сформировать одномерный массив Y из максимальных элементов строк матрицы. Найти произведение элементов массива Y и заменить им угловые элементы матрицы Х. Массивы Х и Y вывести на экран.

5. Дан файл G, компонентами которого являются вещественные числа. Найти сумму и количество компонент, расположенных на нечетных позициях файла. Сумму записать на место первой компоненты файла. Преобразованный файл G, а также найденные сумму и количество распечатать.

ВАРИАНТ 22

1. Составить программу для вычисления функции

где

Значения x и y ввести с клавиатуры.

2. Напечатать таблицу перевода t из градусов шкалы Цельсия (°С) в градусы шкалы Фаренгейта (F) для значений от 1 до 20°С с шагом 1°С (F=1,8С+32).

3. Задан одномерный массив А(N) (N<=60). Найти сумму положительных элементов и произведение отрицательных массива. Если сумма больше произведения, найти максимальный элемент массива, а если нет – выдать об этом сообщение.

4. Дана матрица А (MxN), М<=10, N<=20. Получить вектор B из максимальных элементов строк матрицы А. Поменять местами первый и последний элемент вектора B. Отпечатать полученный вектор

5. Ввести с клавиатуры файл F действительных чисел и выдать его на печать. Определить в нем среднее арифметическое компонентов, стоящих после второй отрицательной компоненты, и записать его в конец файла. Выдать на печать преобразованный файл. Если преобразование невозможно, то дать об этом сообщение.

ВАРИАНТ 23

1. Вычислить и напечатать:

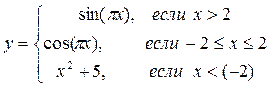
Значение x ввести с клавиатуры.

2. Вычислить и напечатать значения функции и соответствующие им значения аргументов x, y. z=2^xy-2^yx при изменении первого аргумента x[-1;1] с шагом 0.1 и второго аргумента y[2;2] с шагом 0.2.

3. В заданном одномерном массиве X(N) (N<=40) найти наименьшее из четных чисел.

4. Задана матрица Х[N,M], где N<=15, M<=20. Вывести на экран строку матрицы, содержащую максимальный элемент.

5. В файле F заменить все нулевые компоненты значением суммы первой и последней компонент файла; все отрицательные компоненты уменьшить на значение суммы, а также найти среднее арифметическое положительных компонент. Результаты отпечатать.

ВАРИАНТ 24

1. Задано два числа 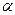и h. При 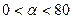вычислить и напечатать 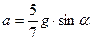. При 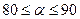вычислить и напечатать 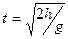. Если же 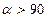, то выдать сообщение: “ 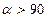” (g - ускорение свободного падения).

2. Вычислить значения функции a=1.6x³-1.5 на интервале (-1,1) с шагом изменения аргумента 0.5. Выдать на печать отрицательные значения функции с соответствующими им значениями аргумента.

3. В заданном одномерном массиве F(N) (N<=50) вычислить разность между суммой элементов, стоящих на четных местах, и суммой элементов, стоящих на нечетных местах.

4. Задана матрица Х[N,M], где N<=15, M<=20. В каждом столбце матрицы подсчитать сумму элементов, расположенных между минимальным и максимальным. Из положительных сумм сформировать одномерный массив Y и вывести его на экран.

5. Дан файл G, компонентами которого являются вещественные числа. Найти в нем максимальную и минимальную компоненты и поменять их местами. Преобразованный файл G распечатать в обратном порядке.

ВАРИАНТ 25

1. Вычислить и напечатать:

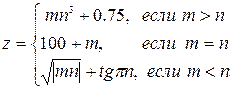
Значения m и n ввести с клавиатуры.

2. Вывести на экран последовательность чисел y, являющихся результатом выполнения следующей операции:

y = Asinx,

где A=0,5, а переменная x изменяется от 1 до 10 с шагом 1.

3. Задан одномерный массив R(N) (N<=60). Получить новый массив Q путём домножения элементов исходного массива R на его минимальный элемент. Вычислить среднее арифметическое полученного массива Q и записать его на место минимального элемента исходного массива R. Результат вывести на экран.

4. Задана матрица Х[N,N], где N<=15. Найти минимальный среди элементов, расположенных ниже главной диагонали. Преобразовать матрицу, разделив положительные её элементы на найденный максимум. Преобразованную матрицу вывести на экран.

5. Дан файл G, компонентами которого являются вещественные числа. Найти сумму и количество компонент, расположенных на нечетных позициях файла. Сумму записать на место первой компоненты файла. Преобразованный файл G, а также найденные сумму и количество распечатать.

ВАРИАНТ 26

1. Дано a, b, c. Вычислить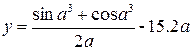

Если y=0, выдать об этом сообщение.

Если y>0, вычислить значение выражения: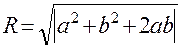

Если R>25, отпечатать R.

Если R£25, вычисления закончить.

Если y<0, отпечатать a, b, c.

2. Составить программу вычисления и вывода на экран значений величин x и y, где

.

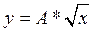Переменная x изменяется в интервале от 1,5 до 7,5 c шагом 0,5, .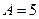

Вывести значения функции > 2 с соответствующим значением аргумента.

3. Задан одномерный массив А(N) (N<=60). Найти сумму положительных элементов и произведение отрицательных массива. Если сумма больше произведения, найти максимальный элемент массива, а если нет – выдать об этом сообщение.

4. Дана матрица А (MxN), М<=10, N<=20. Получить вектор B из максимальных элементов строк матрицы А. Поменять местами первый и последний элемент вектора B. Отпечатать полученный вектор

5. В файле F заменить все нулевые компоненты значением суммы первой и последней компонент файла; все отрицательные компоненты уменьшить на значение суммы, а также найти среднее арифметическое положительных компонент. Результаты отпечатать.